Contents

Modellierung

Lineare Regression

Lineare Regression zu Fuß

Gegeben sind zwei numpy Arrays. Die Daten Zeigen das Verhähltnis zwischen Lernzeit und Note für 10 Studentinnen.

Lernzeit = np.array([2,7,11,17,20,22,30,35,39,41])

Note = np.array([5,5,4,3.7,3,3.7,2.7,2,2.3,1])

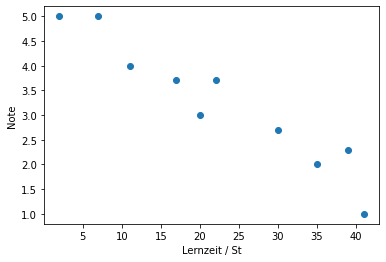
I. Plotten Sie die Daten auf ein Scatter Plot, wobei die Lernzeit auf der X-Achse und der Note auf der Y-Achse aufgetragen werden sollen.

II. Eine lineare Regression sucht die Gerade, die den quadratischen Abstand aller Messwerte zu jener Gerade minimiert. Folgend sind die beiden Formeln für die Steigung \(m\) und den y-Achsenabschnitt \(b\) der gesuchten Gerade. \(n\) ist die Anzahl der Datenpunkte.

\[\begin{split} m &= \frac{(n \cdot \sum xy) - (\sum x \cdot \sum y)}{(n \cdot \sum x^2) - ((\sum x)^2)}\\ b &= \frac{\sum y - (m \cdot \sum x)}{n} \end{split}\]

Berechnen Sie mit den gegebenen Daten und mithilfe der beiden Formeln die Gerade.

III. Speichern Sie die berechnete Gerade in einer Funktion und bennenen Sie diese.

Lösung I

import numpy as np
import matplotlib.pyplot as plt

Lernzeit = np.array([2,7,11,17,20,22,30,35,39,41])
Note = np.array([5,5,4,3.7,3,3.7,2.7,2,2.3,1])

plt.scatter(Lernzeit,Note)
plt.xlabel('Lernzeit / St')
plt.ylabel('Note')
plt.show()
../../../../_images/zusatz_modellierung_5_0.png

Lösung II

#Steigung

x_summe = np.sum(Lernzeit)
y_summe = np.sum(Note)
xy_summe = np.sum(Lernzeit*Note)
xx_summe = np.sum(Lernzeit**2)

m = ((10*xy_summe)-(x_summe*y_summe))/((10*xx_summe)-(x_summe**2))
print(m)

#Achsenabschnitt

b = (y_summe-m*x_summe)/10
print(b)

-0.09101666264187402
5.278773243177978

Lösung III

# y = m*x + b

def zufuss(Stunden):
    return -0.091*Stunden + 5.278

Lineare Regression mit np.polyfit()

Berechnen Sie die Koeffizienten \(m\) und \(b\) mithilfe np.polyfit().

Lösung

polyline = np.polyfit(Lernzeit,Note,1)
polyline

array([-0.09101666,  5.27877324])

Vergleichen der Lösungswege

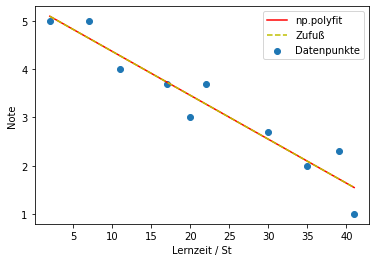
Plotten Sie die Datenpunkte, und beide berechnete Linien mit matplotlib.

Lösung

plt.plot(Lernzeit, polyline[0]*Lernzeit + polyline[1], 'r', label='np.polyfit')
plt.plot(Lernzeit, zufuss(Lernzeit), '--y', label='Zufuß')
plt.scatter(Lernzeit, Note, label='Datenpunkte')
plt.xlabel('Lernzeit / St')
plt.ylabel('Note')
plt.legend()
plt.show()
../../../../_images/zusatz_modellierung_15_0.png

Schätzung

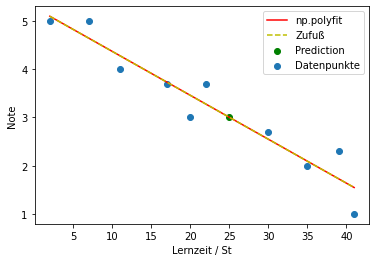
Eine Regression erlaubt es, Erwartungswerte für Punkte zu erhalten, für die man keine Daten hat.
Was wäre die erwartete Note einer Studentin, die 25 Stunden gelernt hat?

Lösung

print(zufuss(25))

plt.scatter(25, zufuss(25), c='g', label='Prediction')

plt.plot(Lernzeit, polyline[0]*Lernzeit + polyline[1], 'r', label='np.polyfit')
plt.plot(Lernzeit, zufuss(Lernzeit), '--y', label='Zufuß')
plt.scatter(Lernzeit, Note, label='Datenpunkte')
plt.xlabel('Lernzeit / St')
plt.ylabel('Note')
plt.legend()
plt.show()

3.0029999999999997
../../../../_images/zusatz_modellierung_18_1.png