3. Interferenz am Gitter

Um zu verstehen, wie die Intensitätsverteilung an einem Gitter aussieht, schauen wir uns zunächst an, was bei \(N\) Einzelstrahlen passiert (siehe Abbildung 3.16).

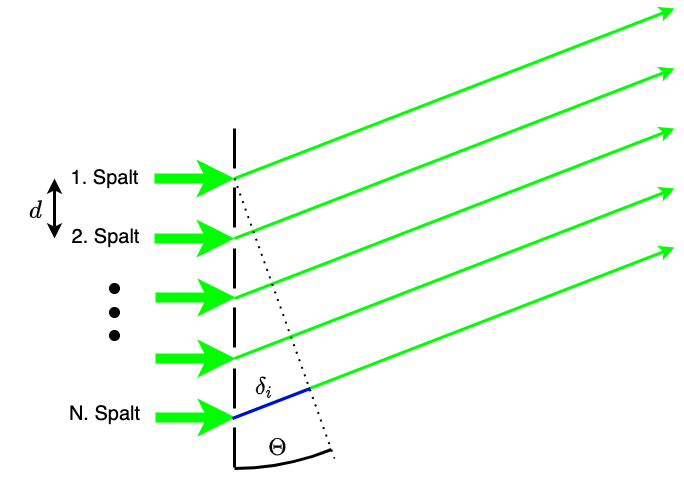
Fig. 3.16 Schematische Darstellung der Überlagerung von \(N\) Einzelstrahlen.

Wellenfunktion für eine Welle aus Spalt \(l\)

\[z_l \left(t,x \right) = \hat{z}_l \cdot e^{i \left(\omega t - kx + \Delta \phi_i \right)} = \hat{z} \cdot e^{ji\left(\omega t - kx + i\cdot \Delta \phi \right)} \]

mit \(\Delta \phi = \frac{2\pi}{\lambda} \cdot d \cdot sin \left(\theta \right)\).

Das bedeutet auf dem Schirm treffen \(N\) Strahlen mit einem Gangunterschied \(\delta_i\) mit \(i = 1..N\) auf. Die daraus resultierende Welle ist dann

\[\begin{split} \begin{eqnarray} z_{ges} \left(t,x \right) &=& \sum_{i=1}^N \hat{z} e^{j \left(\omega t -k x + i \Delta \phi \right)} \\ &=& \hat{z} e^{i \left(\omega t -k x\right)}\sum_{i=1}^N e^{i\left(l \Delta \phi \right)} \\ &=& \hat{z} e^{i \left(\omega t -k x\right)}\sum_{i=1}^N \left( e^{i \Delta \phi} \right)^l \\ &=& \hat{z} e^{i \left(\omega t -k x\right)}\sum_{i=0}^N \left( e^{i\Delta \phi} \right)^{(l-1)} \end{eqnarray} \end{split}\]

Zur Lösung kann die endliche geometrische Reihe (für \(q \le 1\)) verwendet werden.

\[\sum_{l=0}^N q^{n-1} = \frac{q^N - 1}{q - 1} \]

Damit ist

\[\sum_{l=0}^N \left( e^{i\Delta \phi} \right)^{(l-1)} = \frac{e^{i N \Delta \phi} - 1}{e^{i\Delta \phi} -1}\]

und

\[z_{ges} \left(t,x \right) = \hat{z} e^{i \left(\omega t -k x\right)}\frac{e^{i N \Delta \phi} - 1}{e^{i\Delta \phi} -1} = \hat{z}_{int} e^{i \left(\omega t -k x\right)}\]

mit

\[\hat{z}_{int} = \hat{z} \frac{e^{i N \Delta \phi} - 1}{e^{i\Delta \phi} -1} \]

Die Intensitätsverteilung berechnet sich wieder über \(I \propto \hat{z}_{int} \hat{z}_{int}^\ast \). Es gilt:

\[ \left( e^{ix} - 1 \right)\left( e^{-ix} - 1 \right) = e^{ix-ix} - e^{ix} - e^{-ix} + 1 = e^0 - \left( e^{ix} + e^{-ix} \right) + 1 = 2 - \left( e^{ix} + e^{-ix} \right) = 2 - 2 \cdot cos\left( \frac{x}{2} \right)\]

mit

\[cos(x) = 1-2\cdot sin^2\left(\frac{x}{2} \right) \Leftrightarrow 1 - cos(x) = 2\cdot sin^2\left(\frac{x}{2} \right)\]

ist dann

\[ \left( e^{ix} - 1 \right)\left( e^{-ix} - 1 \right) = 2 - 2 \cdot cos\left( \frac{x}{2} \right) = 2 \left(1 - cos(x) \right) = 4 sin^2 \left( \frac{x}{2}\right) \]

Damit ist dann

\[\begin{split} \begin{eqnarray} \hat{z}_{int} \hat{z}_{int}^\ast &=& \left(\hat{z}\frac{e^{i N \Delta \phi} - 1}{e^{i\Delta \phi} -1}\right) \left(\hat{z} \frac{e^{i N \Delta \phi} - 1}{e^{i\Delta \phi} -1}\right)^\ast \\ &=& \hat{z}\hat{z}^\ast \frac{\left( e^{i N \Delta \phi} - 1\right) \left(e^{- i N \Delta \phi} - 1\right)}{\left( e^{i\Delta \phi} -1\right) \left( e^{-i\Delta \phi} -1\right)} \\ &=& \hat{z}\hat{z}^\ast \frac{4 sin^2 \left( \frac{1}{2}N \Delta \phi\right)}{4 sin^2 \left( \frac{1}{2}\Delta \phi\right)} \\ &=& \hat{z}\hat{z}^\ast \frac{sin^2 \left( \frac{1}{2}N \Delta \phi\right)}{sin^2 \left( \frac{1}{2}\Delta \phi\right)} \end{eqnarray} \end{split}\]

Die Intensitätsverteilung von \(N\) sich überlagernden Strahlen mit Abstand \(d\) und daraus resultierender Phasenverschiebung \(\Delta \phi = \frac{2\pi}{\lambda} \cdot d \cdot sin \left(\theta \right)\) und \(I_0 = \hat{z}\hat{z}^\ast\) ist somit

\[ \begin{equation} \Rightarrow I = I_0 \frac{sin^2 \left( \frac{N \pi d}{\lambda} sin (\theta) \right)}{sin^2 \left( \frac{\pi d}{\lambda} sin (\theta) \right)} \end{equation} \]

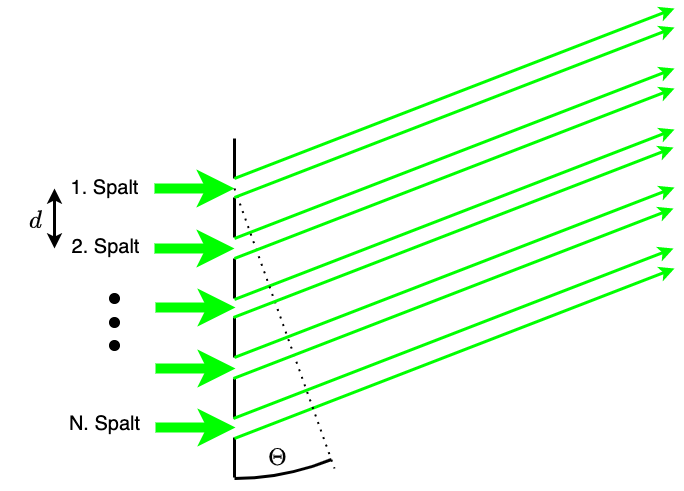
Fig. 3.17 Schematische Darstellung der Interferenz am Gitter.

Wie in Abbildung 3.17 dargestellt ist, findet man bei einem Gitter aber nicht \(N\) einzelne Strahlen, sondern \(N\) Spalte mit endlicher Breite \(b\) und Spaltabstand \(d\). Die resultierende Intensität an einem Gitter ist also eine Überlagerung aus der Intensitätsverteilung an einem Einzelspalt und der Verteilung, welche aus der Überlagerung von \(N\) Strahlen her resultiert. Die Interferenzverteilung am Gitter ist als

\[ \begin{equation} \Rightarrow I_{Gitter} = \frac{I_0}{N^2} \frac{sin^2 \left( \frac{\pi \cdot b}{\lambda} \cdot sin \left( \theta \right)\right) }{\left(\frac{\pi\cdot b}{\lambda} sin(\theta) \right)^2} \frac{sin^2 \left( \frac{N \pi d}{\lambda} sin (\theta) \right)}{sin^2 \left( \frac{\pi d}{\lambda} sin (\theta) \right)} \end{equation} \]

Abbildung Abbildung 3.18 und Abbildung 3.19 zeigen zeigt die Intensitätsverteilung an einem Gitter mit \(N=5\) und an dem einfachsten Gitter, dem Doppelspalt mit \(N=2\). Wie zu erkennen ist, führen die Spalte dazu, dass es neben den Hauptmaxima weitere \(N-2\) Nebenmaxima gibt.

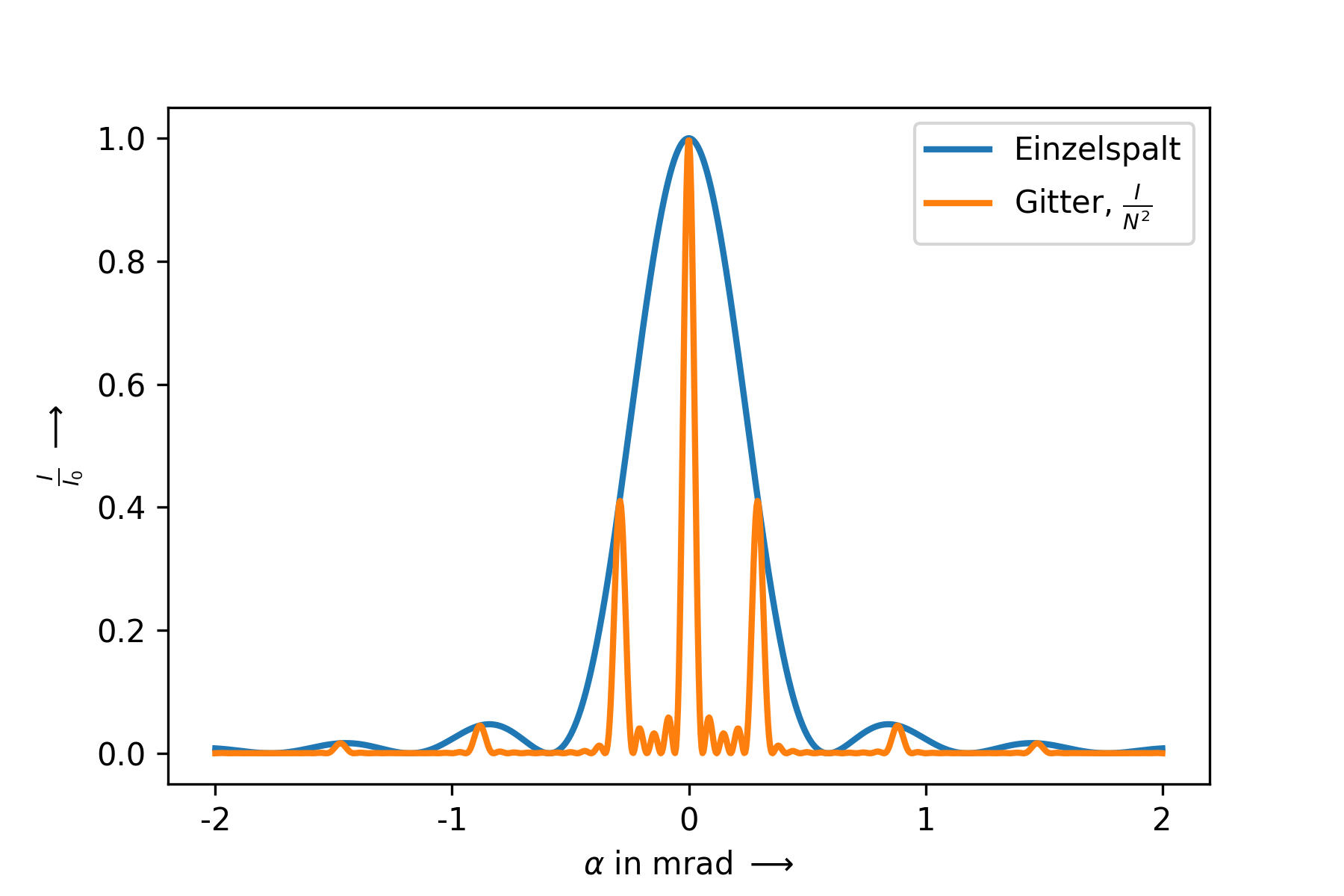
Fig. 3.18 Gitter mit \(N = 5\) im Vergleich zum Einzelspalt mit \(\frac{1}{N^2}\) der Gesamtintensität.

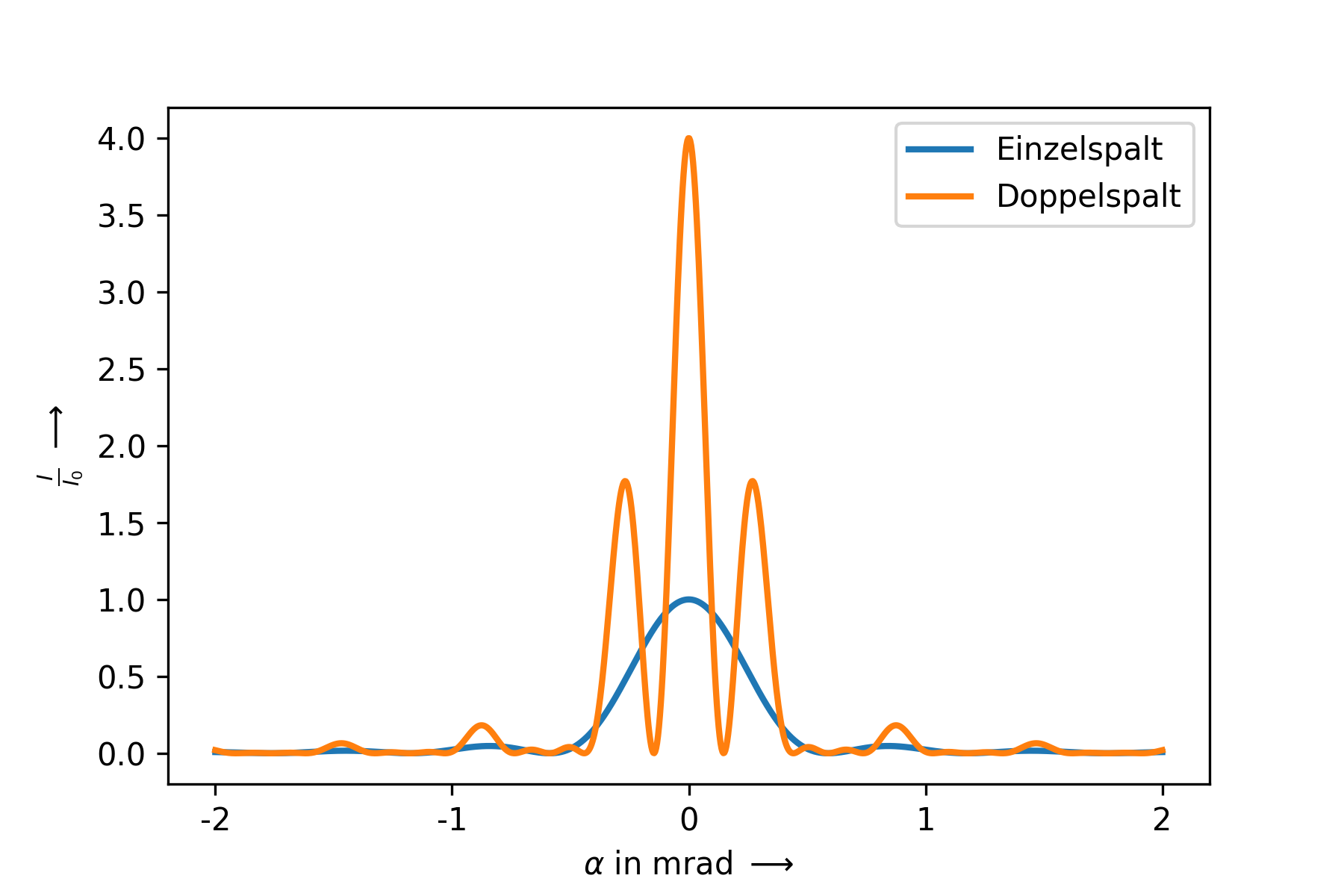
Fig. 3.19 Doppelspalt (Gitter mit \(N=2\)) im Vergleich zum Interferenzmuster eines Spaltes des Gitters.

Zusammenfassend kann gesagt werden, dass

• Die Intensitäten der Hauptmaxima sind größer also bei Einzelspalt

• Die Hauptmaxima sind schmaler.

• Es existieren sehr intensitätsschwache Nebenmaxima.

Bei optischen Gittern wir der Abstand von jeweils zwei benachbarten Spaltmitten auch als Gitterkonstante bezeichnet. Oft wird auch die Anzahl der Spalte (“Striche”) pro \(mm\) angegeben.

Fig. 3.20 Beispiel: weisses Licht am Doppelspalt. In der Mitte das Hauptmaximum (für alle Wellenlängen gleich, daher weiss). Das 1. Hauptmaximum liegt für jede Wellenlänge an einer andere Stelle \(\longrightarrow\) Aufspaltung in Spektralfarben!

Optische Gitter haben viele Anwendungsbereiche.

Wellenlängenmessung

Mit einem Gitter kann beispielsweise durch Messung der Abstände der Hauptmaxima die Wellenlänge des verwendeten Lichtes bestimmt werden.

Spektralanalyse

Fällt Licht mehrerer Wellenlängen auf das Gitter, so zeigen die unterschiedlichen Wellenlängen Interferenzmuster mit unterschiedlichen Abständen der Maxima. Licht lässt sich also in seine Spektralfarben zerlegen. Durch Messungen der farbspezifischen Abstände der Maxima kann ermittelt werden, welche Wellenlängen zum Spektrum beitragen.