5. Erzwungene Schwingung

Erzwungene Schwingungen sind Schwingungen, die durch einen äußeren Impuls angetrieben werden. Zu Beginn der erzwungenen Schwingung findet ein Einschwingvorgang statt, der darin begründet ist, dass die sich die Schwingung des Systems (ein gedämpfter harmonischer Oszillator) und die von aussen angelegte Schwingung sich überlagern, sich die Bewegungen durch die Massenträgheit aber nicht sprunghaft ändern können. Der Einschwingvorgang ist komplex und wird im Rahmen der Vorlesung nicht betrachtet. Weiterführende Informationen sind beispielsweise hier zu finden. Nach einem Einschwingvorgang wird ein neuer stationärer Zustand erreicht, in dem das System mit derselben Frequenz wie der Treiber schwingt. Wenn der Einschwingvorgang praktisch abgeschlossen ist, nimmt das System also einen eingeschwungenen Zustand an, Amplitude und Energie bleiben dann konstant. In diesem stationären Zustand ist die Energie, die dem System durch die treibende Kraft pro Schwingung zugeführt wird, gleich der durch die Dämpfung dissipierten Energie, die pro Schwingung verloren geht.

Die Differentialgleichung der erzwungenen Schwingung verändert sich dahingehend, als dass auf der rechten Seite nun die Funktion der von außen angelegten Schwingung steht. Angenommen, diese äußere Schwingung hat die Frequenz \(\omega\) und die Amplitude \(F\), so kann diese Erregerschwingung beschrieben werden durch

\[F(t) = F cos \left(\omega t \right)\]

Die zu lösende Differentialgleichung ist damit

\[m \frac{d^2x}{dt^2} + \beta \frac{dx}{dt} + ky = F cos \left(\omega t \right)\]

Diese kann auch dargestellt werden als

\[\frac{d^2x}{dt^2} + \frac{\beta}{m} \frac{dx}{dt} + \frac{k}{m}x = \frac{F}{m} cos \left(\omega t \right)\]

oder mit \(2\delta = \frac{\beta}{m}\)

(5.1)\[\frac{d^2x}{dt^2} + 2\delta \frac{dx}{dt} + \omega_0^2x = \frac{F}{m} cos \left(\omega t \right)\]

Die Lösung dieser Differentialgleichung ist einfacher im Komplexen. Nach der Eulerschen Formel gilt

\[e^{i\omega t} = cos(\omega t) + i sin(\omega t)\]

Somit ist \(cos(\omega t) = Re \left( e^{i \omega t} \right)\).

Die Variable \(x\) wird nun durch die komplexe Variable \(z = Re(z) + i Im(z)\) ersetzt. Die DGL im Komplexen lautet also

\[\frac{d^2z}{dt^2} + 2\delta \frac{dz}{dt} + \omega_0^2z = \frac{F}{m} e^{i\omega t}\]

Als Lösungsansatz wird wieder eine e-Funktion verwendet. Damit ist

\[z(t) = Ae^{i\left( \omega t + \phi\right)}\]

und

\[\frac{dz(t)}{dt} = i \omega A e^{i\left( \omega t + \phi\right)}\]

und

\[\frac{d^2 z(t)}{dt^2} = - \omega^2 A e^{i\left( \omega t + \phi\right)} \]

Mit \(\delta = \frac{\beta}{2m}\) und \(\omega_0 = \sqrt{\frac{k}{m}}\)

Einsetzt in die DGL (5.1) ergibt sich daraus

\[\frac{d^2z}{dt^2} + 2\delta \frac{dz}{dt} + \omega_0^2z = \frac{F}{m} e^{i\omega t} \Leftrightarrow - \omega^2 A e^{i\left( \omega t + \phi\right)} + 2\delta i A \omega e^{i\left( \omega t + \phi\right)} + \omega_0^2 A e^{i\left( \omega t + \phi\right)} = \frac{F}{m} e^{i\omega t}\]

\[\Leftrightarrow \left(\omega_0^2 - \omega^2 \right)A e^{i\left( \omega t + \phi\right)} + 2\delta i A \omega e^{\left( \omega t + \phi\right)} = \frac{F}{m} e^{i\omega t} \Leftrightarrow \left(\omega_0^2 + 2\delta i \omega - \omega^2 \right)A e^{i\left( \omega t + \phi\right)} = \frac{F}{m} e^{i\left( \omega t + \phi\right)} e^{-i\phi}\]

Da die Gleichung für alle \(t\) gilt, muss

\[A\left(\omega_0^2 + 2\delta i \omega - \omega^2 \right)= \frac{F}{m} e^{-i\phi} = \frac{F}{m} \left(cos (\phi) - i sin (\phi)\right)\]

gelten. Die Gleichung hat einen Realteil und einen Imaginärteil, welche separat voneinander verglichen werden können.

Realteil

\[ A\left(\omega_0^2 - \omega^2 \right) = \frac{F}{m} cos (\phi)\]

Imaginärteil

\[2 A \delta \omega = -\frac{F}{m} sin (\phi)\]

Dies ergibt ein Gleichungssystem mit zwei Gleichungen und 2 Unbekannten, welches gelöst werden kann. Auflösen nach \(A\) und \(\phi\) ergibt

(5.2)\[ A\left(\omega_0^2 - \omega^2 \right) = \frac{F}{m} cos (\phi)\]

und

(5.3)\[2 A \delta \omega = \frac{F}{m} sin (\phi)\]

Mit Gleichung (5.2) geteilt durch Gleichung (5.3)

\[\frac{\frac{F}{m} sin (\phi)}{\frac{F}{m} cos (\phi)} = \frac{- 2 A \delta \omega}{A\left(\omega_0^2 - \omega^2 \right)} \Leftrightarrow \frac{sin (\phi)}{cos (\phi)} = tan(\phi) = \frac{-2 \delta \omega}{\left(\omega_0^2 - \omega^2 \right)} \]

\[\Leftrightarrow \phi = arctan \left(- \frac{2 \delta \omega}{\omega_0^2 - \omega^2 } \right) = - arctan \left( \frac{2 \delta \omega}{\omega_0^2 - \omega^2 } \right)\]

Damit ist

\[\left| \phi \right|= arctan \left( \frac{2 \delta \omega}{\omega_0^2 - \omega^2 } \right)\]

Mit Gleichung (5.2)\(^2\) + Gleichung (5.3)\(^2\) ergibt sich für die Amplitude der erzwungenen Schwingung:

\[\left( A\left(\omega_0^2 - \omega^2 \right) \right)^2 + \left( 2 A \delta \omega \right)^2= \left(\frac{F}{m} cos (\phi) \right)^2 + \left( \frac{F}{m} sin (\phi) \right)^2\]

\[A^2\left(\left(\omega_0^2 - \omega^2 \right) ^2 + \left( 2\delta \omega \right)^2 \right) = \left(\frac{F}{m} \right)^2 \left(cos^2 (\phi) + sin^2 (\phi) \right)= \left(\frac{F}{m} \right)^2\]

(5.4)\[A = \frac{\frac{F}{m}}{\sqrt{\left(\omega_0^2 - \omega^2 \right) ^2 + \left( 2\delta \omega \right)^2 }}\]

5.1. Resonanz

Die Amplitude der erzwungenen Schwingung ist nach (5.4)

\[A = \frac{\frac{F}{m}}{\sqrt{\left(\omega_0^2 - \omega^2 \right) ^2 + \left( 2\delta \omega \right)^2 }}\]

Wie zu erkennen ist, ist diese Amplitude abhängig von der Eigenfrequenz des Systems (\(\omega_0\)) und der Frequenz der externen Erregerschwingung (\(\omega\)). Bei einer bestimmten Frequenz der externen Erregerschwingung wird diese Amplitude maximal. Man spricht dann vom Resonanzfall und die zugehörige Frequenz wird als Resonanzfrequenz bezeichnet.

Zur Bestimmung dieser Resonanzfrequenz, muss das Maximum der Gleichung (5.4) bestimmt werden. Dazu wird die Ableitung nach \(\omega\) gebildet und gleich 0 gesetzt \(\frac{d A (\omega)}{d\omega} = 0\).

\(\frac{d A (\omega)}{d\omega} = \frac{d A (\omega)}{d\omega} \frac{F}{m}\left(\left(\omega_0^2 - \omega^2 \right) ^2 + \left( 2\delta \omega \right)^2 \right)^{-1/2}\)

\(= \frac{F}{m}\left(\left(\omega_0^2 - \omega^2 \right) ^2 + \left( 2\delta \omega \right)^2 \right)^{-3/2}\frac{d}{d\omega}\left( \left(\omega_0^2 - \omega^2 \right) ^2 + \left( 2\delta \omega \right)^2 \right)\)

\( = \frac{F}{m}\left(\left(\omega_0^2 - \omega^2 \right) ^2 + \left( 2\delta \omega \right)^2 \right)^{-3/2} \left( 2\left(\omega_0^2 - \omega^2 \right)(-2\omega) + 2 \left( 2\delta \omega \right)2\delta \right)\)

Mit

\(\frac{d A (\omega)}{d\omega} = 0\)

\(\Leftrightarrow \frac{F}{m}\left(\left(\omega_0^2 - \omega^2 \right) ^2 + \left( 2\delta \omega \right)^2 \right)^{-3/2} \left( 2\left(\omega_0^2 - \omega^2 \right)(-2\omega) + 2 \left( 2\delta \omega \right)2\delta \right) = 0\)

\(\Leftrightarrow \left( 2\left(\omega_0^2 - \omega^2 \right)(-2\omega) + 2 \left( 2\delta \omega \right)2\delta \right) = 0\)

\(\Rightarrow 4 \omega \left( -\left(\omega_0^2 - \omega^2 \right) + 2 \delta^2 \right) = 0\)

Also ist neben der trivialen Lösung \(\omega = 0\) noch die Lösung

\(\Rightarrow 4 \omega \left( -\left(\omega_0^2 - \omega^2 \right) + 2 \delta^2 \right) = 0\)

möglich. Hieraus ergibt sich die Resonanzfrequenz

\[\omega_R = \sqrt{\omega_0^2 - 2 \delta^2}\]

Die Abhängigkeit der Resonanzfrequenz von der Dämpfung ist in Abbildung 4.3 dargestellt. Je geringer die Dämpfung ist, desto größer ist die Amplitude bei Resonanzfrequenz. Wäre keinerlei Dämpfung vorhanden, würde die Amplitude unendlich groß werden (Resonanzkatastrophe).

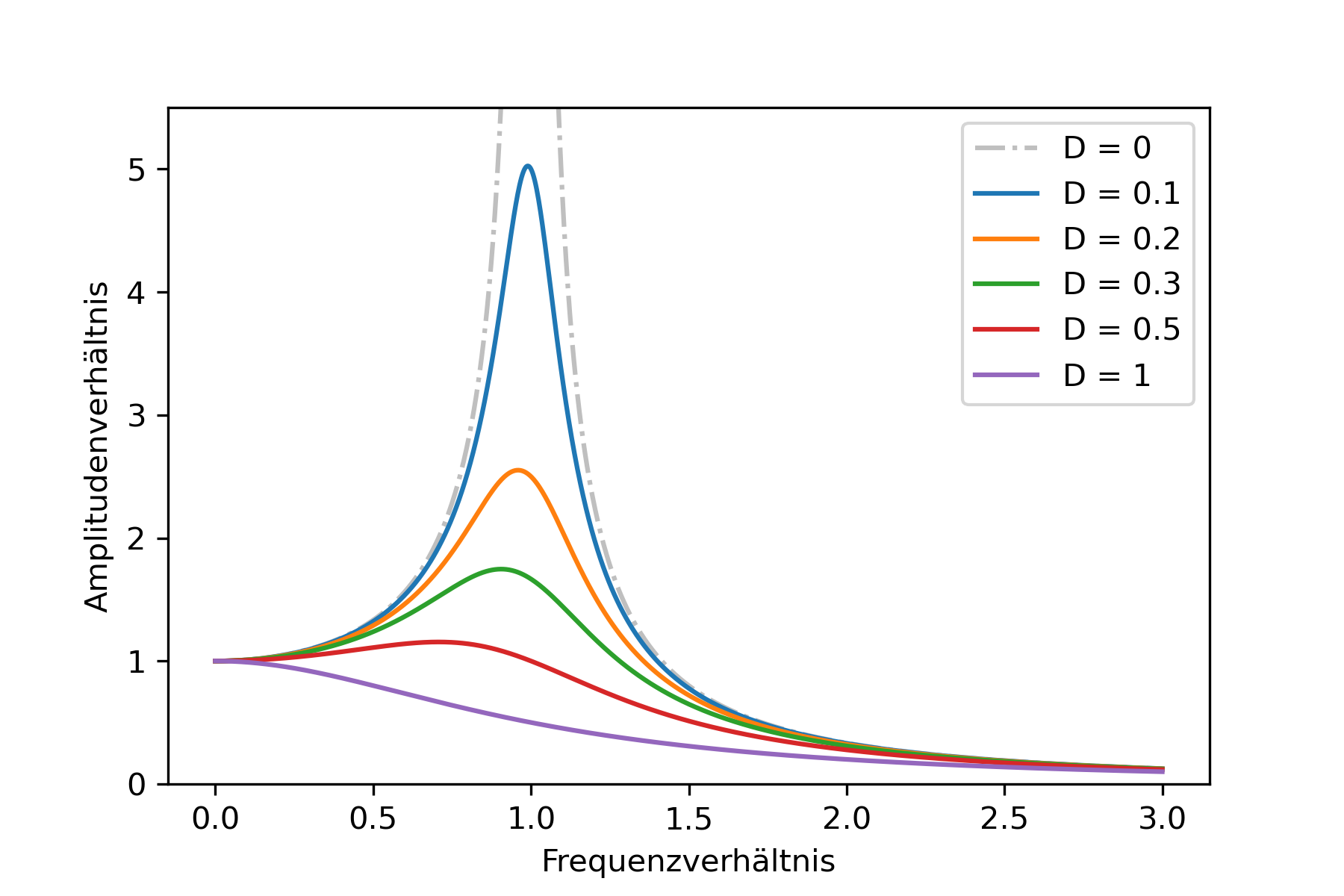
Fig. 5.1 Resonanzfrequenz bei verschiedenen Dämpfungsgraden.

Ein schönes digitales “Experiment” zur erzwungenen Schwingung ist hier zu finden.