3. Federpendel

Eine der einfachsten Pendelbewegungen ist das Federpendel. Das Federpendel führt eine eindimensionale Pendelbewegung durch, die durch eine harmonische Schwingung beschrieben werden kann.

Fig. 3.1 Federpendel, Quelle: Oleg Alexandrov - self-made with en:Matlab., Gemeinfrei

Im folgenden wird zunächst am Beispiel des Federpendels die grundlegende harmonische Schwingungsgleichung betrachtet und danach darauf aufbauend die gedämpfte und die erzwungene Schwingung.

3.1. Bewegungsgleichung des Federpendels

Das Federpendel ist eine Masse, die an einer Feder aufgehangen ist. Vereinfacht kann dieses Konstrukt als Punktmasse an einer masselosen Feder betrachtet werden, so das die Pendelbewegung alleine durch die Bewegung des Schwerpunktes beschrieben werden kann. Die Voraussetzung für eine mechanische Schwingung erfüllt das Federpendel in folgender Weise:

• Es muss mind. ein schwingungsfähiger Körper vorhanden sein. \(\longrightarrow\) Massepunkt

• Der oder die schwingungsfähigen Körper müssen zu Beginn der Schwingung aus ihrer Ruhelage ausgelenkt sein, oder sie müssen eine von Null verschiedene Anfangsgeschwindigkeit haben \(\longrightarrow\) Anfangsbedingung \(x(t = 0 ) = x_0\)

• Es müssen rücktreibende Kräfte vorhanden sein, die bewirken, dass sich der oder die Körper nach der Auslenkung wieder in Richtung Ruhelage bewegen \(\longrightarrow\) Hook’sches Gesetz

Das Hook’sche Gesetz beschreibt, mit welcher Kraft eine Feder ihrer Auslenkung entgegenwirkt. Für diese Kraft gilt

\[F_{R} = - k\cdot x\]

wobei k die sogenannte Federkonstante ist. Je größer die Federkonstante, desto stärker die rückstellende Kraft. Je größer die Auslenkung ist, desto größer ist die rückstellende Kraft. Das Minuszeichen stellt sicher, dass die Kraft ihrer Auslenkung entgegenwirkt.

Fig. 3.2 Federpendel ohne Gravitation

Abbildung Abbildung 3.2 zeigt die Auslenkung eines Federpendels zu 5 unterschiedlichen Zeitpunkten. Diese werden im folgenden nun einzeln betrachtet.

1. Die Feder wird auseinandergezogen, die Auslenkung \(x\) ist somit positiv. Die Rückstellkraft wirkt der Auslenkung entgegen und wirkt somit in negative x-Richtung \(F_R = -k\cdot x\)

2. Die Auslenkung ist \(x=0\), die Masse hat eine Geschwindigkeit in \(-x \text{-Richtung}\). Es wirkt keine Rückstellkraft in diesem Punkt

3. Die Masse hat eine negative Auslenkung. Die Feder wird zusammengedrückt und die Rückstellkraft wirkt in positive x-Richtung \(F_R = - k\cdot x\)

4. Die Auslenkung ist \(x=0\), die Masse hat eine Geschwindigkeit in \(x \text{-Richtung}\). Es wirkt keine Rückstellkraft in diesem Punkt

5. Die Feder wird auseinandergezogen, die Auslenkung \(x\) ist somit positiv. Die Rückstellkraft wirkt der Auslenkung entgegen und wirkt somit in negative x-Richtung \(F_R = -k\cdot x\)

Die Bewegung ist in Punkt 5 demnach wieder am gleichen Punkt wie zu Beginn angekommen und startet erneut.

Um die Bewegung mathematisch zu beschreiben, kann eine Kräftebilanz aufgestellt werden.

Allgemein gilt

\[F_{ges} = \sum_i F_i\]

In diesem Fall ist

\[F_{ges} = m\cdot a = m\cdot \ddot{x}\]

da es sich um eine eindimensionale Bewegung handelt. Auf die Masse wirkt nur die Rückstellkraft der Feder, damit ist

\[\sum_i F_i = - k \cdot x\]

Damit gilt

\[m\cdot \ddot{x} = - k \cdot x\]

oder auch

\[\ddot{x} + \frac{k}{m} \cdot x = 0\]

Dies ist eine Differentialgleichung. Ihre Lösung liefert die Bewegungsgleichung der Masse. Es wird also eine Funktion gesucht, deren zweifache Ableitung sich nur durch eine Konstante \(\frac{k}{m}\) von der unsprünglichen Funktion unterscheidet. Daher ist eine e-Funktion ein guter Ansatz für eine derartige Differenzialgleichung.

\[x(t) = c \cdot e^{\lambda \cdot t}\]

\[\dot{x}(t) = \lambda \cdot c \cdot e^{\lambda \cdot t}\]

\[\ddot{x}(t) = \lambda^2 \cdot c \cdot e^{\lambda \cdot t}\]

Damit ist

\[\lambda^2 \cdot c \cdot e^{\lambda \cdot t} + \frac{k}{m} \cdot c \cdot e^{\lambda \cdot t} = 0\]

\[\Leftrightarrow c \cdot e^{\lambda \cdot t} \left(\lambda^2 + \frac{k}{m}\right)\]

\[\Rightarrow \lambda^2 + \frac{k}{m} = 0\]

\[ \lambda = \pm i\sqrt{\frac{k}{m}} := \pm i\omega_0\]

mit \(\omega_0 = \sqrt{\frac{k}{m}}\).

Es gibt also zwei mögliche Lösungen für diese Differentialgleichung. Die Lösung ist die Summe aller möglichen Lösungen und somit ist

\[x(t) = c_1 \cdot e^{i\omega_0 \cdot t} + c_2 \cdot e^{-i\omega_0 \cdot t}\]

Die Konstanten \(c_1\) und \(c_2\) können aus den Anfangsbedingungen bestimmt werden. Angenommen, die Anordnung ist zum Zeitpunkt t = 0 so, wie zum Zeitpunkt 1 in Abbildung Abbildung 3.2, dann gilt

\[x\left(t = 0\right) = \hat{x} \text{ und } x \left( t\cdot \omega_0 = \frac{\pi}{2}\right)\]

Damit ist

(3.1)\[x\left(t = 0\right) = c_1 \cdot e^{i\omega_0 \cdot 0} + c_2 \cdot e^{-i\omega_0 \cdot 0} = c_1 + c_2 = \hat{x}\]

und

\[x \left( t\cdot \omega_0 = \frac{\pi}{2}\right) = c_1 \cdot e^{i\frac{\pi}{2}} + c_2 \cdot e^{-i \frac{\pi}{2}} = 0\]

Die e-Funktion lässt sich nach der Eulersche Formel auch schreiben als

\[e^{i \phi} = cos \left(\phi \right) + i sin \left(\phi \right)\]

Damit ist

\[c_1 \cdot e^{i\frac{\pi}{2}} + c_2 \cdot e^{-i \frac{\pi}{2}} = 0\]

\[\Leftrightarrow c_1 \cdot \left(cos ( \frac{\pi}{2}) + i sin ( \frac{\pi}{2}) \right) + c_2 \cdot \left(cos ( - \frac{\pi}{2}) + i \cdot sin (- \frac{\pi}{2}) \right) = 0\]

\[\Leftrightarrow c_1 \cdot \left(cos ( \frac{\pi}{2}) + i sin ( \frac{\pi}{2}) \right) + c_2 \cdot \left(cos (\frac{\pi}{2}) - i \cdot sin (\frac{\pi}{2}) \right) = 0\]

\[\Leftrightarrow cos ( \frac{\pi}{2}) \cdot \left(c_1 + c_2 \right) + i\cdot sin (\frac{\pi}{2}) \left(c_1 - c_2\right) = 0\]

Mit \(cos ( \frac{\pi}{2}) = 0\) und \(sin (\frac{\pi}{2}) = 1\) ist dann

\[\left(c_1 - c_2\right) = 0 \Leftrightarrow c_1 = c_2\]

Dies in und Gleichung (3.1) eingesetzt ergibt

\[2 \cdot c_1 = 2 \cdot c_2 = \hat{x} \Leftrightarrow c_1 = c_2 = \frac{\hat{x}}{2}\]

Damit ist die Lösung der Differentialgleichung mit den oben beschriebenen Anfangsbedingungen

\[x(t) = \frac{\hat{x}}{2} \cdot \left(e^{i \omega_0 t} + e^{-i \omega_0 t}\right) = \hat{x} \cdot cos \left( \omega_0 t\right)\]

Allgemein für beliebige Anfangsbedingungen gilt

\[x(t) = \hat{x} \cdot cos \left( \omega_0 t + \phi \right)\]

Da Sinus und Cosinus sich nur durch eine Phasenverschiebung von \(180^\circ\) unterscheiden, kann auch

\[x(t) = \hat{x} \cdot sin \left( \omega_0 t + \tilde{\phi} \right)\]

geschrieben werden mit \(\phi = \tilde{\phi} + 90^\circ\).

Das Video Abbildung 3.3 zeigt die Bewegung eines Federpendel (oder auch harmonischen Oszillators) mit einer Amplitude von \(\hat{x}=1\) und einer Frequenz von \(\omega = 1\) (Klick auf das Bild startet das Video).

Federpendel

Fig. 3.3 Ortskurve (Bewegungsgleichung) eines Federpendels, bzw. harmonischer Oszillators.

3.2. Geschwindigkeit und Beschleunigung des harmonischen Oszillators.

Die Geschwindigkeit und die Beschleunigung des harmonischen Oszillators lassen sich aus den aus der Kinematik bekannten Zusammenhängen herleiten. Für die Geschwindigkeit gilt:

\[v(t) = \frac{dx(t)}{dt} = \frac{d}{dt} \left(\hat{x} \cdot cos \left(\omega_0 t \right)\right) = - \omega_0 \cdot\hat{x} \cdot sin \left(\omega_0 t \right)\]

Für die Beschleunigung gilt

\[a(t) = \frac{dv(t)}{dt} = \frac{d}{dt} \left( - \omega_0 \cdot\hat{x} \cdot sin \left(\omega_0 t \right)\right) = - \omega_0^2 \cdot\hat{x} \cdot cos \left(\omega_0 t \right)\]

Beim Nulldurchgang ist also die Geschwindigkeit des Massenpunktes maximal, im Nullpunkt ist die Beschleunigung jedoch =0, hier ist der Massenpunkt kräftefrei. An den Umkehrpunkten ist die Geschwindigkeit = 0, die Beschleunigung ist jedoch maximal und in Richtung des Nulldurchgangs der Schwingung gerichtet. Das Video Abbildung 3.4 zeigt Ortskurve, Geschwindigkeit und Beschleunigung eines Federpendel mit einer Amplitude von \(\hat{x}=1\) und einer Frequenz von \(\omega = 1\) (Klick auf das Bild startet das Video).

Federpendel

Fig. 3.4 Ortskurve, Geschwindigkeit und Beschleunigung eines Federpendels, bzw. harmonischer Oszillators.

3.3. Harmonischer Oszillator mit Gravitation

Bislang wurde ein Federpendel ohne den Einfluss der Gravitation betrachtet. In der Realität wirkt diese jedoch auf der Erde und muss somit in die Betrachtung mit aufgenommen werden.

Die Gravitationskraft wirkt zusätzlich zu der durch das Hook’sche Gesetz beschriebenen Federkraft. In der Nähe der Erdoberfläche kann diese Gravitationskraft also konstant mit einer konstanten Erdbeschleunigung von \(g = 9.81 \, \frac{m}{s^2}\) angenommen werden. Die Kräftebilanz muss in diesem Fall erweitert werden auf

\[\sum_i F_i = - k \cdot x - m\cdot g\]

Damit wird die Kräftebilanz zu:

\[m \ddot{x} = - k \cdot x - m\cdot g\]

und die zu lösende Differentialgleichung wird zu

\(\ddot{x} + \frac{k}{m} \cdot x + g = 0\)$

Da der Term \(g\) konstant ist, kann die Gleichung vereinfacht werden, indem eine neue Variable \(\tilde{x}\) definiert wird mit

\[\tilde{x} = x + \frac{m}{k}g\]

mit dieser Variablen gilt

\[x = \tilde{x} - \frac{m}{k}g\]

und

\[\ddot{x} = \frac{d^2}{dt^2} \left(\tilde{x} - \frac{m}{k}g\right) = \ddot{\tilde{x}}\]

Damit wird die Differentialgleichung zu

\[\ddot{\tilde{x}} + \frac{k}{m} \cdot \tilde{x} = 0\]

Diese Differentialgleichung hat exakt die gleiche Struktur wie im Fall ohne Gravitation und somit ebenfalls die Lösung

\[\tilde{x}(t) = \hat{\tilde{x}} \cdot cos \left( \omega_0 t + \phi \right) = \hat{x} \cdot cos \left( \omega_0 t + \phi \right) - \frac{m}{k}g\]

Die (konstante) Gravitation führt daher lediglich zu einer gesamten Verschiebung der Schwingung um \(- \frac{m}{k}g\).

Federpendel

Fig. 3.5 Vergleich der Ortskurve eines Federpendels, bzw. harmonischer Oszillators ohne und mit Einfluss der (konstanten) Gravitation.

3.4. Energie des harmonischen Oszillators

Das reibungsfreie Federpendel (harmonischer Oszillator) führt eine Pendelbewegung aus, bei der kinetische Energie in Spannenergie umgewandelt wird und umgekehrt. In diesem System sind also die kintische und potenzielle Energie des Systems zeitabhängig. Ihre Summe, die mechanische Gesamtenergie $\(E = E_{kin}(t) + E_{spann}(t)\)$ ist jedoch konstant.

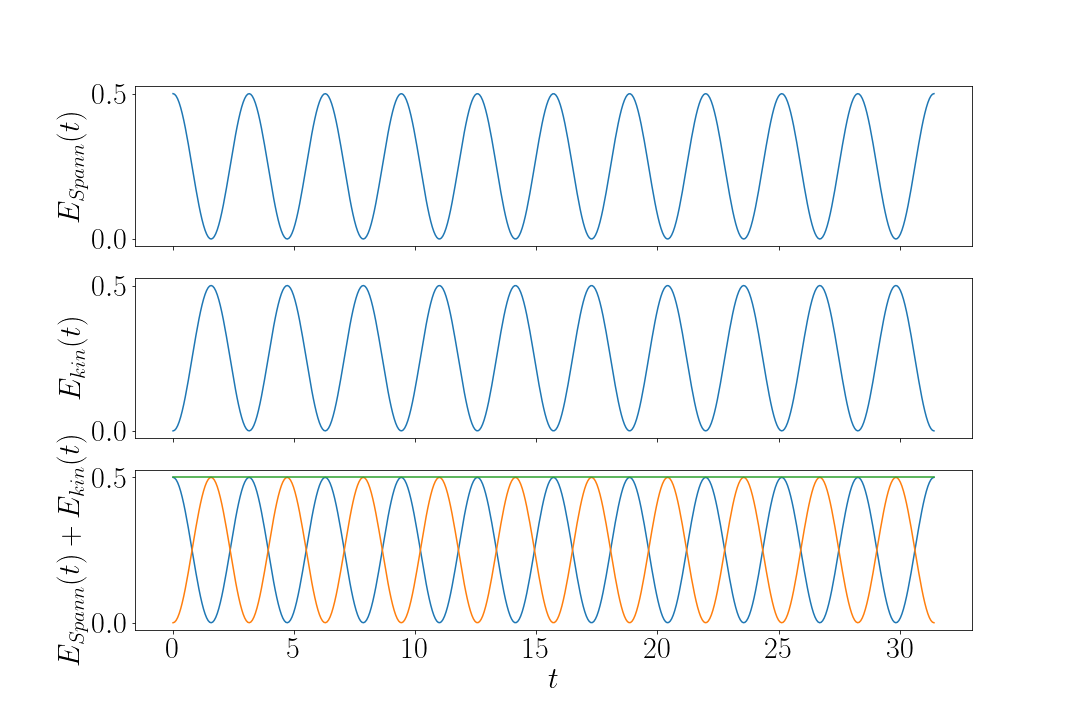
Fig. 3.6 Mechanische Energie des harmonischen Oszillators

Für die kinetische Energie des harmonischen Oszillators gilt:

\[E_{kin} = \frac{1}{2} m v^2 = \frac{1}{2} m \left( - \omega_0 \cdot\hat{x} \cdot sin \left(\omega_0 t \right)\right)^2 = \frac{m\omega_0^2}{2}\left(\hat{x} \cdot sin \left(\omega_0 t + \phi \right)\right)^2 \]

Für die Spannenergie des harmonischen Oszillators gilt:

\[E_{spann} = \frac{1}{2} k x^2 = \frac{1}{2} k \left( \hat{x} \cdot cos \left( \omega_0 t + \phi \right) \right)^2 = \frac{k}{2} \left( \hat{x} \cdot cos \left( \omega_0 t + \phi \right) \right)^2\]

Für die gesamte mechanische Energie des harmonischen Oszillators gilt dann

\[E = E_{kin}(t) + E_{spann}(t) = \frac{m\omega_0^2}{2}\left(\hat{x} \cdot sin \left(\omega_0 t + \phi \right)\right)^2 + \frac{k}{2} \left( \hat{x} \cdot cos \left( \omega_0 t + \phi \right) \right)^2\]

Da für \(\omega_0\) der Zusammenhang \(\omega_0 = \sqrt{\frac{k}{m}}\) gilt, ist \(k = \omega_0^2 \cdot m\). Damit lässt sich die Gesamtenergie des harmonischen Oszillators zusammenfassen zu

\[E = \frac{m\omega_0^2}{2}\left(\hat{x} \cdot sin \left(\omega_0 t + \phi \right)\right)^2 + \frac{\omega_0^2 \cdot m}{2} \left( \hat{x} \cdot cos \left( \omega_0 t + \phi \right) \right)^2\]

\[\Rightarrow E = \frac{m\omega_0^2}{2}\hat{x}^2 \cdot \left( \left(sin \left(\omega_0 t + \phi \right)\right)^2 + \left( cos \left( \omega_0 t + \phi \right) \right)^2\right)\]

mit \(sin^2 + cos^2 = 1\) wird dies zu

\[E = \frac{m\omega_0^2}{2}\hat{x}^2 = \frac{k}{2}\hat{x}^2 \]