Physikalisches Pendel

7. Physikalisches Pendel#

Bislang wurde ein mathematisches Pendel bestrachtet, d.h. ein Pendel, welches durch eine schwingende Masse an einem masselosen Faden beschrieben werden kann. Bei ausgedehnten Massen, insbesondere, wenn die Drehachse sich mit geringerem Abstand zum Schwerpunkt befindet oder sogar innerhalb der Masseverteilung liegt, ist eine Näherung durch ein mathematisches Pendel nicht mehr möglich. In einem solchen Fall kann die Schwingung durch das Modell des physikalischen Pendels (siehe Abbildung 7.1) beschrieben werden.

Ein physikalisches Pendel ist:

Ein ausgedehnter starrer Körper, der sich frei um eine horizontale Achse drehen kann, die nicht durch seinen Schwerpunkt S verläuft
Es beginnt nach einer Auslenkung aus seiner Gleichgewichtslage zu schwingen.

Die Bewegung kann als Pendelbewegung des Schwerpunktes des starren Körpers beschrieben werden. Wie auch bei anderen Drehbewegungen von starren Körpern, muss das Drehmoment betrachtet werden. Dies bedeutet, dass der Abstand zwischen Schwerpunkt und Drehachse relevant ist.

physikalisches Pendel — Fig. 7.1 Schematische Darstellung eines physikalischen Pendels.#

Abbildung 7.1 zeigt schematisch dargestellt die Pendelbewegung und die wirkenden Kräfte. Die Gewichtskraft greift dabei am Schwerpunkt des Pendels an. Das resultierendes Drehmoment, welches durch die Bewegung des Schwerpunktes um die Drehachse erzeugt wird ist gegeben durch:

$\vec{M} = \vec{r} \times \vec{F}$

$\Rightarrow M = - d\cdot mg \cdot sin \left(\phi\right)$

Ebenso kann das wirkende Drehmoment über das Trägheitsmoment des Pendels berechnet werden. Demnach gilt für das Drehmoment:

\[M = \Theta \alpha = \Theta \frac{d^2\phi}{dt^2}\]

Damit gilt

\[\Theta \frac{d^2\phi}{dt^2} = - d\cdot m \cdot g \cdot sin \left(\phi\right)\]

\[\frac{d^2\phi}{dt^2} = - \frac{d}{\Theta }\cdot m \cdot g \cdot sin \left(\phi\right)\]

Wie schon beim mathematischen Pendel ist diese Differentialgleichung analytisch nur für kleine Winkel lösbar. Für kleine Winkel gilt die Näherung

\[sin \left( \phi \right) \approx \phi\]

Damit vereinfacht sich die Differentialgleichung zu

\[\frac{d^2\phi}{dt^2} = - \frac{d}{\Theta }\cdot m \cdot g \cdot sin \left(\phi\right) \longrightarrow \frac{d^2\phi}{dt^2} = - \frac{d}{\Theta }\cdot m \cdot g \cdot \phi\]

Die Lösung dieser Differentialgleichung ergibt die Bewegungsgleichung des physikalischen Pendels für kleine Winkel.

Als Lösungsansatz kann wie beim mathematischen Pendel folgender Ansatz verwendet werden:

$\phi(t) = c_1\cdot e^{i\cdot c_2 \cdot t}$

$ \Rightarrow \frac{d\phi(t)}{dt} = c_1\cdot i \cdot c_2\cdot e^{i\cdot c_2 \cdot t} $

$\Rightarrow \frac{d^2\phi(t)}{dt^2} = - c_1 \cdot c_2^2\cdot e^{i\cdot c_2 \cdot t} = - \frac{d}{\Theta }\cdot m \cdot g \cdot \phi = - \frac{d}{\Theta }\cdot m \cdot g \cdot c_1\cdot e^{i\cdot c_2 \cdot t}$

Damit kann $c_2$ einfach bestimmt werden:

\[c_2^2 = \frac{d}{\Theta }\cdot m \cdot g \Rightarrow c_2 = \pm \sqrt{\frac{d}{\Theta }\cdot m \cdot g} \]

Die Lösung der Differentialgleichung ist die Summe aller möglichen Lösungen

\[\phi(t) = c_1\cdot e^{i\cdot \frac{mg}{l} \cdot t} + c_1\cdot e^{- i\cdot \frac{mg}{l} \cdot t}\]

mit

\[\omega = \sqrt{\frac{d}{\Theta }\cdot m \cdot g} \]

ergibt sich hieraus

\[\phi(t) = c_1\left(e^{i\cdot \omega \cdot t} + \cdot e^{- i\cdot \omega \cdot t}\right) = 2c_1\left(cos \left( \omega \cdot t\right)\right)\]

aus der Anfangsbedingung $\phi (t = 0) = \hat{\phi}$ ergibt sich dann $$2c_1 =: \hat{\phi}$$

und somit

\[\phi(t) = \hat{\phi} \left(cos \left( \omega \cdot t\right)\right)\]

Allgemeine Bewegungsgleichung (für beliebige Anfangsbedingungen) ist:

\[\phi(t) = \hat{\phi}\left(cos \left( \omega \cdot t\right)+ \delta\right)\]

Mit $\hat{\phi}$ : maximale Winkelauslenkung des Pendels

$\omega$ : Kreisfrequenz der Schwingung

$\delta$ : Phasenverschiebung

Es gilt der Zusammenhang

$\omega = \sqrt{\frac{d}{\Theta }\cdot m \cdot g} $

und somit

(7.1)#\[\omega = \frac{2 \pi}{T} \Leftrightarrow T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{\Theta }{d\cdot m \cdot g}} \]

7.1. Beispiel: Schwingung eines Stabpendels#

Also Beispiel wird im Folgenden ein einfaches Stabpendel betrachtet. Die Schwingungsdauer des physikalischen Pendels ist nach (7.1)

\[T = 2\pi \sqrt{\frac{\Theta }{d\cdot m \cdot g}}\]

Das Trägheitsmoment eines (langen Stabes) ist bezüglich seines Schwerpunktes ist

\[\Theta_S = \frac{1}{12} m l^2 \]

Da die Drehachse den Abstand $d$ zum Schwerpunkt hat, muss der Satz von Steiner angewendet werden.

\[\Theta_S = \frac{1}{12} m l^2 + m \cdot d^2\]

Damit ist die Schwingungsdauer

\[T = 2\pi \sqrt{\frac{ \frac{1}{12} m l^2 + m \cdot d^2 }{d\cdot m \cdot g}} = 2\pi \sqrt{\frac{ \frac{1}{12} l^2 + d^2 }{d \cdot g}}\]

Die Schwingungsdauer eines $1\, m$ langen Stabpendels ist in Abbildung 7.1 zu sehen. Bei ungefähr $\frac{1}{4} l$ ist die Schwingungsdauer minimal, bei größeren und kleineren Abständen nimmt die Schwingungsdauer zu. Für $d \longrightarrow 0$ geht die Schwingungsdauer gegen unendlich, für $d \longrightarrow \infty$ gegen die Schwingungsdauer des mathematischen Pendels.

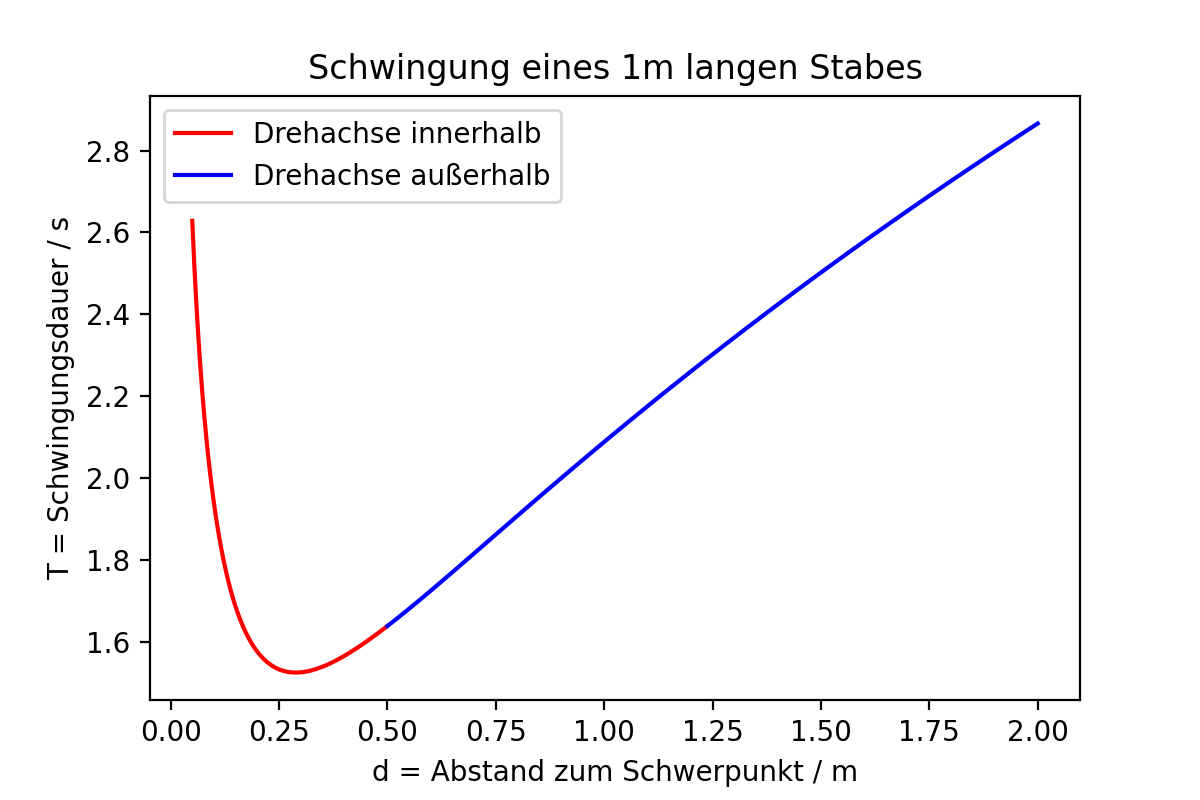
Physikalisches Pendel

Contents

7. Physikalisches Pendel#

7.1. Beispiel: Schwingung eines Stabpendels#