1. Spektrometrie#
Allgemein ist ein Spektrum die Verteilungsfunktion einer physikalischen Größe. Die bedeutet, auf der x-Achse ist die betrachtete Physikalische Größe aufgetragen, im Falle von elektromagnetischen Wellen, wie beispielsweise Licht, wäre dies die Frequenz oder die Wellenlänge. Auf der y-Achse wird dann ein Megenmaß aufgetragen, also eine Größe, die beschreibt, wie stark eine bestimmte Frequenz oder Wellenlänge vertreten ist. Dies kann im Fall von Elektromagnetischen Wellen die Intensität sein. In der Bildbearbeitung arbeitet man auch häufig mit Spektren. Hier werden Sie als Histrogramm bezeichnet und stellen die Häufigkeitsverteilung der Helligkeit einer bestimmten Wellenlänge (blau, grün oder rot) dar.
1.1. Schwarzkörperstrahlung#
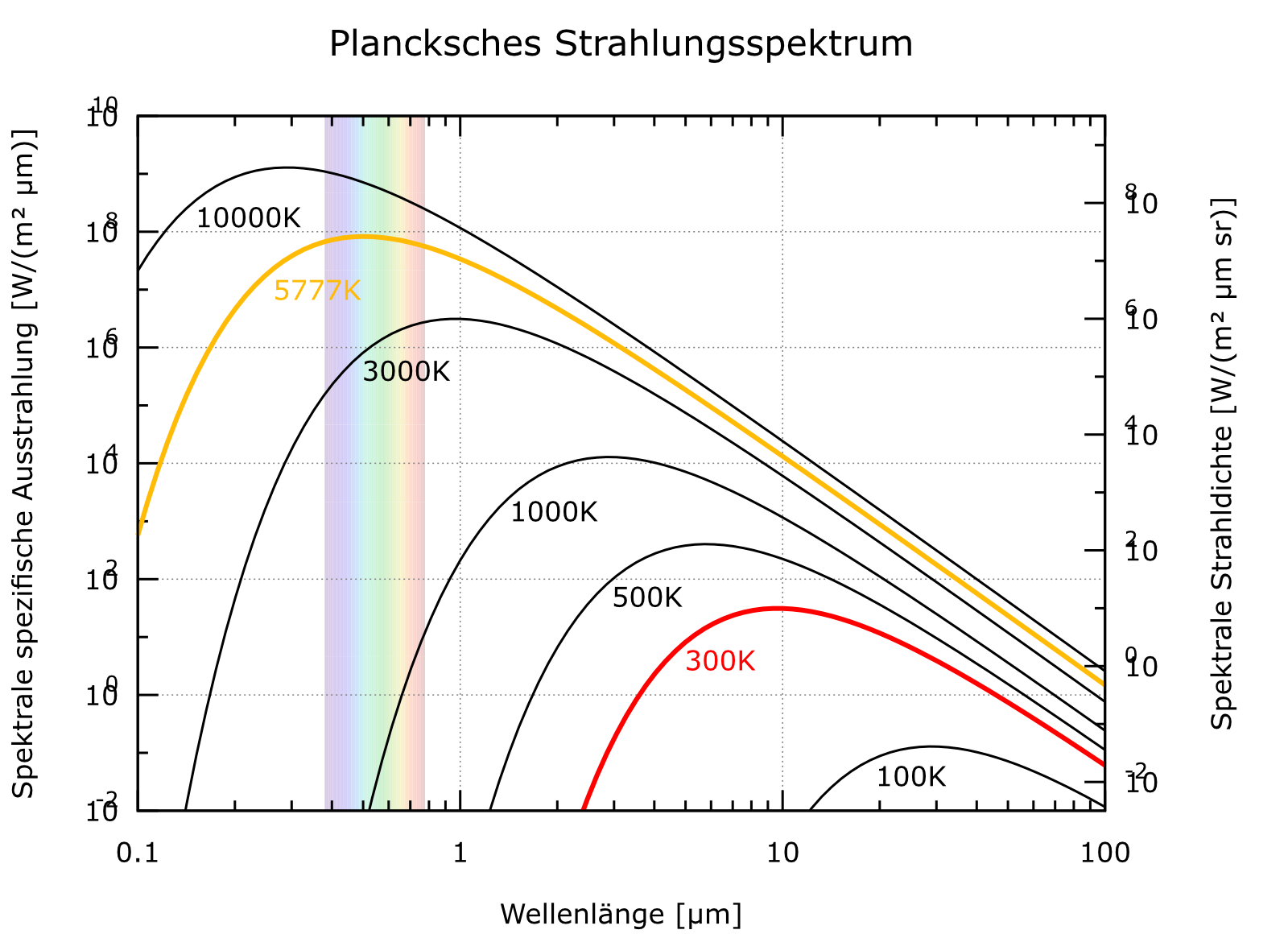
Fig. 1.5 Emissionsspektrum eines schwarzen Körpers, Quelle: Prog, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=60809691#
Jeder Körper absorbiert und emittiert elektromagnetische Strahlung (Wärmestrahlung). Das Spektrum, also die Verteilung der Strahlung wird durch das Stephan-Boltzmann-Gesetz beschrieben.
mit der Stefan-Boltzmann-Konstante \( \sigma \approx 5. 67\cdot 10^{-8}\, \frac{W}{m^2 K^4} \).
Wenn sich ein Körper in thermischem Gleichgewicht mit seiner Umgebung befindet, befindet sich Absorption und Emission im Gleichgewicht. Eine derartige Strahlungsquelle bezeichnet man als schwarzen Strahler, da er alle Wellenlängen absorbiert. In Realität werden meist nicht alle Wellenlängen absorbiert, jedoch stellt die Näherung als schwarzer Strahler vielfach eine gute Näherung dar (siehe auch Abbildung 1.8. Die Wärmestrahlung, die ein schwarzer Körper aussendet hängt in ihrer Intensität und spektralen Verteilung nur von der Temperatur des schwarzen Körpers ab.
Vorstellen kann mich sich das ganze mit Hilfe der Strahlung durch einen Hohlraum.
In einem warmen Hohlraum mit Wänden aus beliebigem, nichttransparentem Material, die auf einer konstanten Temperatur gehalten werden, geben die Wände Wärmestrahlung ab und es stellt sich ein Strahlungsgleichgewicht ein. Die elektromagnetische Strahlung, die den Hohlraum erfüllt, nennt man Hohlraumstrahlung. Die Energiedichte und die Frequenzverteilung der Hohlraumstrahlung hängt nur von der Temperatur der Wände ab und weist dieselbe Energiedichte und dasselbe Spektrum wie die Strahlung eines Schwarzen Körpers auf. Außerdem ist die Strahlung homogen, isotrop, unpolarisiert und vom Volumen des Hohlraums unabhängig.
Bringt man in der Hohlraumwand eine Öffnung an, die klein genug ist, um das thermische Gleichgewicht nicht merklich zu stören, so absorbiert der Hohlraum nahezu ideal die einfallende Strahlung, und durch die Öffnung tritt nur thermische Strahlung aus. Die von der Öffnung ausgehende Strahlung hat dann die Eigenschaften eines Schwarzen Körpers, wenn die Öffnung klein gegenüber dem Innenvolumen ist. Dabei kann der Reflexionsgrad der inneren Hohlraumoberfläche wesentlich größer als null sein. Von außen in den Hohlraum einfallende Strahlung wird dann im Inneren vielfach hin und her reflektiert und dabei zum größten Teil absorbiert und nur zu einem kleinen Rest wieder durch Reflexionen ausgestrahlt.
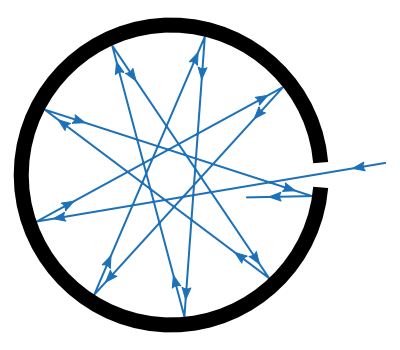
Fig. 1.6 Hohlraumstrahlung, Quelle: AG Caesar, CC BY-SA 4.0 https://commons.wikimedia.org/w/index.php?curid=67057188#
Daher wird die Schwarzkörperstrahlung auch als Hohlraumstrahlung bezeichnet.
Das Stefan-Bolzmann-Gesetz (1.1) beschreibt die gesamte Strahlungsleistung des schwarzen Körpers. Die Verteilung der Strahlungsleistung über die einzelnen Frequenzen wird durch die Planck’sche Strahlungsformel beschrieben.
Dieses Gesetz kann auch als Funktion der Wellenlänge ausgedrückt werden. Dann wird es zu
Je nach Temperatur des schwarzen Körpers, emittiert dieser eine anderes Frequenzspektrum. Umgekehrt kann man durch Messung des emittierten Frequenzspektrums auf die Temperatur des schwarzen rückschließen.
Das Strahlungsmaxium hängt ebenfalls von der Verteilung ab. Die Position des Maximums lässt sich mit Hilfe des Wien’schen Verschiebungsgesetzes berechnen.
oder für Frequenzen
1.1.1. Beispiel: Mensch#
Ein Mensch hat eine Körpertemperatur von \(36^\circ C\). Abbildung 1.7 zeigt das dazugehörende Spektrum. Im sichtbaren Licht wird kein Licht emittiert, stattdessen liegt der Hauptbereich der spektralen Verteilung im infraroten. Das Maximum liegt bei einer Frequenz von
Dieser Spektralbereich kann durch spezielle Wärmebildkameras sichtbar gemacht werden.
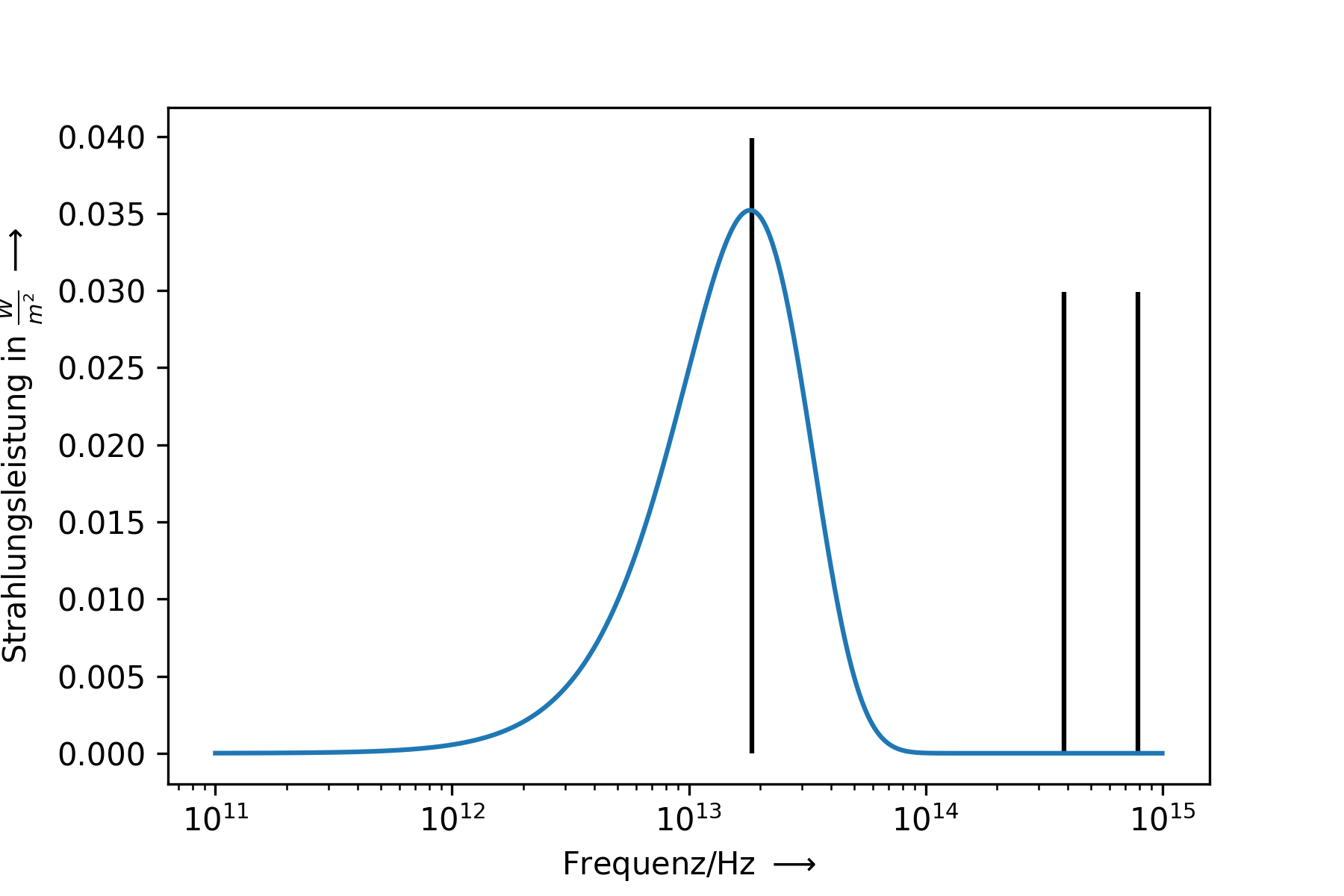
Fig. 1.7 Spektrale Verteilung für \(T=36^\circ C\), was der Körpertemperatur eines Menschen entspricht. Die x-Achse ist logarithmisch skaliert. Die schwarzen senkrechten Balken rechts markieren den Bereich des sichtbaren Spektrums. Der schwarze Strich in der Mitte markiert die Frequenz mit der maximalen Abstrahlung.#
1.1.2. Beispiel: Sonne#
Die Sonne hat eine mittlere Temperatur von \(T = 5777 K\). Abbildung 1.8 zeigt die spektrale Verteilung der solaren Bestrahlungsstärke. Der Vergleich des theoretisch berechneten Verteilung auf Grundlage der Modellvorstellung des schwarzen Körpers mit der realen spektralen Verteilung zeigt, wie gut die theoretische Näherung ist.
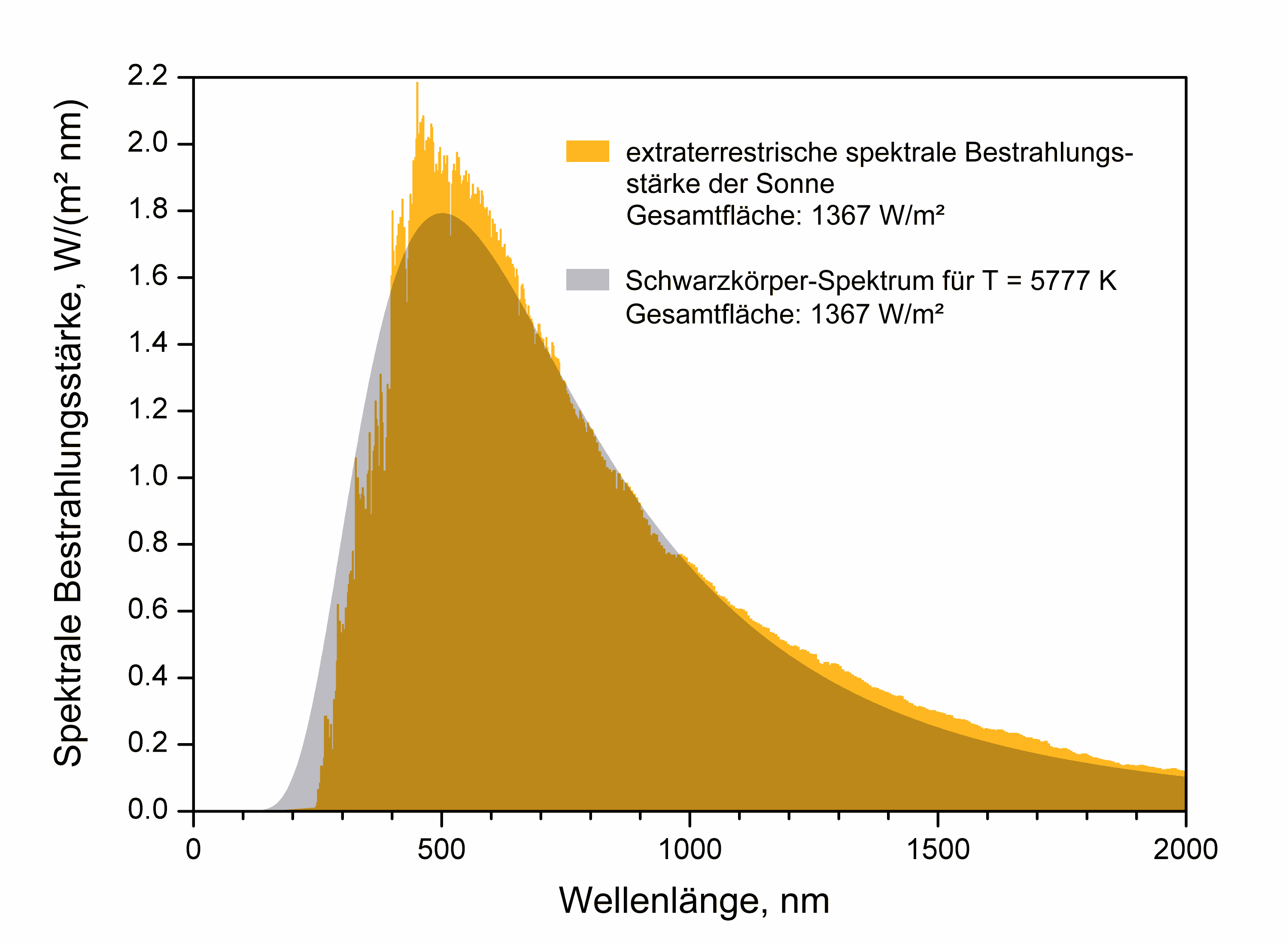
Fig. 1.8 Sonnenspektrum nach dem WRC-Spektrum in M. Iqbal: An Introduction to Solar Radiation, Academic Press 1983, Tabelle C1. Spektrale Bestrahlungsstärke des Schwarzen Körpers berechnet aus Planckspektrum für T gleich 5777 K und Quellenausdehnung 6.8e-5 steradian (Sonnenscheibe), Quelle: Sch, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=758154#
Das Maximum der Verteilung liegt bei
was grünem Licht entspricht. Wieso leuchtet die Sonne dann nicht grün? Weil sie im gesamten Farbspektrum recht gleichmäßig strahlt und das Sonnenlicht somit weiß erscheint. Oft nimmt man die Sonne als gelben Stern war. Dies liegt daran, dass die Sonne zu hell ist, um sie direkt anzuschauen. Man kann nur Richtung Sonne blicken, wenn sie näher am Horizont steht. Dann muss ihr Licht einen längeren Weg durch die Atmosphäre gehen \(\longrightarrow\) Rotverschiebung.
1.2. Emissions- und Absorptionsspektren, Spektroskopie#
Das Spektrum der Schwarzkörperstrahlung zeigt einen kontinuierlichen Verlauf. Dies bedeutet, dass des innerhalb durch die Temperatur vorgegebenen Bereichs Licht in jeder Wellenlänge emittiert wird, es gibt keine “Löcher” in der Verteilung und die einzelnen Farben im Spektrum gehen fließend ineinander über.
Dies ist aber nicht immer so. Beispielsweise das Licht einer Natriumdampflampe oder auch einer Quecksilberdampflampe emittiert aufgrund der atomaren Struktur nur Licht bestimmter Wellenlinien.
Man spricht hier von diskreten Emissionsspektren bzw. Linienspektren. Diese bestehen aus einzelnen, voneinander getrennten dünnen Linien. Die Spektrallinien sind charakteristisch für ein Atom bzw. Molekül.
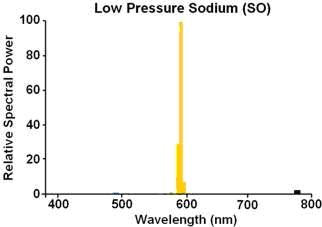
Fig. 1.9 Emissionsspektren einer Natriumdampflampe, Philips Lighting, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=3511896#
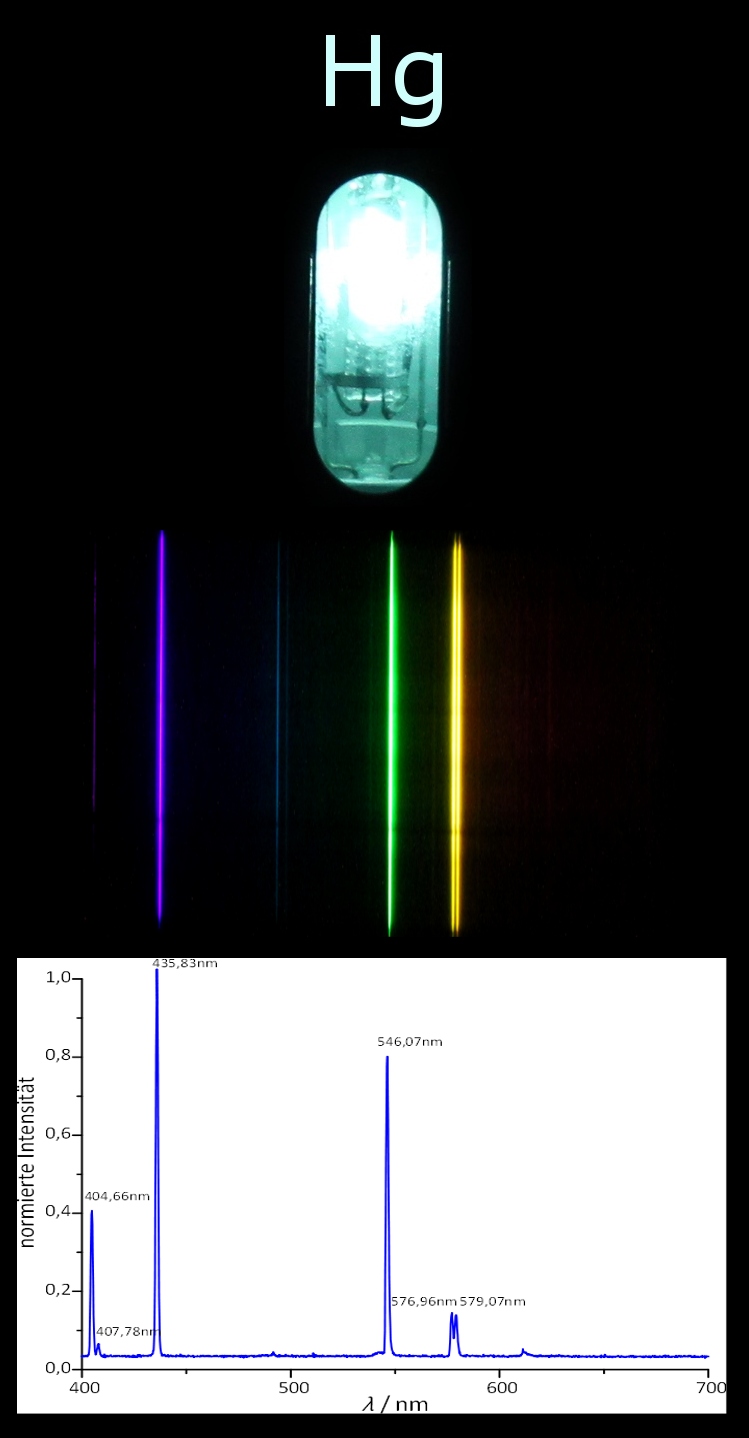
Fig. 1.10 Emissionsspektren einer Quecksilberdampflampe, Sheevar, CC BY-SA 3.0 \href{https://commons.wikimedia.org/w/index.php?curid=14253822#
Umgekehrt können Atome und Moleküle Licht bestimmter Wellenlängen absorbieren, diese Wellenlängen hängen von der atomaren Struktur ab. Es entsteht, wenn Licht mit einem kontinuierlichen Spektrum Materie durchstrahlt und Photonen bestimmter Wellenlängen oder Wellenlängenbereiche dabei absorbiert werden. Diesen Wellenlängen oder Wellenlängenbereiche fehlen im hindurchtretenden Licht. Ein berühmtes Beispiel sind die Fraunhoferlinien (siehe Abbildung 1.11 des Sonnenlichtes. Die Fraunhoferlinien erlauben Rückschlüsse auf die chemische Zusammensetzung und Temperatur der Gasatmosphäre der Sonne.
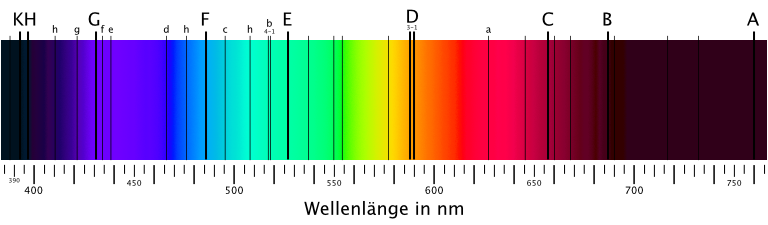
Fig. 1.11 Fraunhofer Absorptionsspektrum im Sonnenlicht, Quelle: NASA, Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=27972#
Die Analyse und Auswertung von Spektrallinien bezeichnet man als Spektroskopie. Mit ihrer Hilfe kann man beispielsweise auch die chemische Zusammensetzung von Lichtquellen untersuchen, ohne Zugang zu der Lichtquelle haben zu müssen.
1.2.1. Beispiel: NDIR CO2 Messung#
Ein Beispiel für eine spektroskopische Methode zur Messung eines bestimmten Gases ist die sogenannte nichtdispersive Infrarotspektroskopie mit Hilfe eines NDIR-Sensors. Ein nichtdispersiver Infrarotsensor oder NDIR-Sensor ist ein spektroskopisches Gerät, das überwiegend als Gassensor eingesetzt wird. Die Funktionsweise wird im folgenden am Beispiel einer CO2 Messung erklärt.
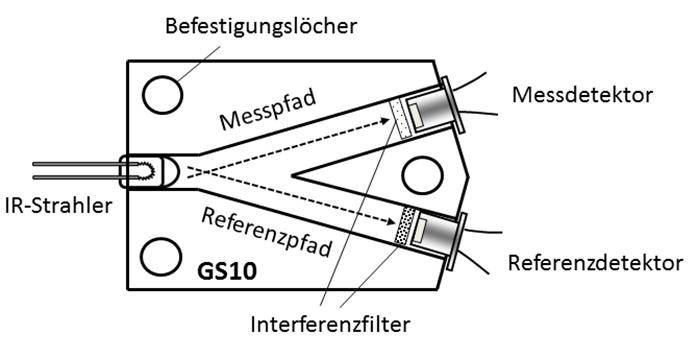
Fig. 1.12 Funktionsweise eines nichtdispersiven Infrarotsensors, http://gasmesstechnik-wiegleb.de/?page_id=50#
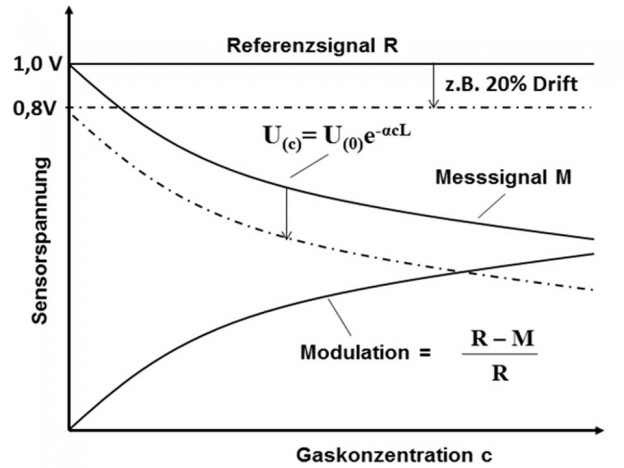
Fig. 1.13 Funktionsweise eines nichtdispersiven Infrarotsensors, http://gasmesstechnik-wiegleb.de/?page_id=50#
Ein NDIR Sensor hat als Eintrittsfenster ein Interferenzfilter mit einer Durchlasskurve im Maximum \(\lambda_M\) der Gasabsorption (siehe Abbildung 1.12), während ein zweiter Detektor als Referenz dient. Die Wellenlänge der Referenzmessung \(\lambda_R\) liegt bei \(\approx 4 \, \mu m\), da dort keine Absorptionsbanden für CO2 vorhanden sind. Befindet sich kein CO2 zwischen der Infrarotquelle und dem Detektor, trifft die emittierte Strahlung nahezu ungehindert auf den Detektor und generiert dort das maximal mögliche Signal. Mit zunehmender C02-Konzentration erhöht sich die Absorption auf auf der für CO2 typischen Absorptionswellenlänge von \(\lambda_M = 4,3 \, \mu m\) und der Detektor misst ein geringeres Signal. Das Referenzsignal dient zur Kalibrierung der Messung. Abbildung 1.13 zeigt auf der rechten Seite das Messsignal und das Referenzsignal als Funktion der CO2-Konzentration. Durch die Höhe des Messsignals kann auf die CO2 Konzentration zurückgeschlossen werden.
