4. Gedämpfte Schwingung

Bislang wurde ein reibungsfreies Federpendel betrachtet. In Realität stellt dies natürlich nur eine Näherung dar, da immer Reibungskräfte auftreten. Der Einfluss von solchen Reibungskräften auf die Pendelbewegung wird im folgenden betrachtet.

Reibung führt dazu, dass ein Teil der Energie in Wärme umgewandelt wird. Dem schwingenden System wird daher durch Reibungskräfte mechanische Energie entzogen. Daher nimmt bei einer realen Schwingung die mechanische Energie mit der Zeit ab. Diesen Effekt nennt man Dämpfung und die entsprechende Schwingung dazu nennt man gedämpfte Schwingung.

Diese Reibungskraft kann durch das Gesetz von Stokes beschrieben werden.

\[F_R = - \beta \cdot v = -\beta \cdot \frac{dx}{dt}\]

Hierbei ist \(\beta\) eine Konstante, die vom Partikelradius und der Viskosität abhängt. Die Reibungskraft wird als der Bewegung proportional zur Geschwindigkeit entgegen.

Die Kräftebilanz des ungedämpften Falles muss daher nun um diesen Term erweitert werden, um die gedämpfte Schwingung zu betrachten.

\[m \ddot{x} = - \beta \dot{x} - kx\]

oder auch

\[\ddot{x} + \frac{\beta}{m} \dot{x} - \frac{k}{m}x = 0\]

mit \(\delta = \frac{\beta}{2m}\) und \(\omega_0 = \sqrt{\frac{k}{m}}\) wird die Differentialgleichung zu

(4.1)\[ \frac{d^2x}{dt^2} + 2\delta\frac{dx}{dt} + \omega_0^2 x = 0\]

Die Lösung dieser Differentialgleichung liefert die Bewegungsgleichung für die gedämpfte Schwingung.

Als Lösungsansatz kann in diesem Fall wieder eine e-Funktion verwendet werden.

\[x(t) = A\cdot e^{\lambda t} \]

\[\Rightarrow \frac{dx}{dt} = A\lambda e^{\lambda t}\]

\[\Rightarrow \frac{d^2x}{dt^2} = A\lambda^2 e^{\lambda t}\]

Eingesetzt in die Differentialgleichung ergibt sich

\[A\lambda^2 e^{\lambda t} + 2\delta A\lambda e^{\lambda t} + \omega_0^2 A e^{\lambda t} = 0 \Leftrightarrow \left(\lambda^2 + 2\delta \lambda + \omega_0^2 \right) \cdot A\cdot e^{\lambda t} = 0\]

Damit dies für alle Zeiten \(t\) gültig ist, muss

\[\lambda^2 + 2\delta \lambda + \omega_0^2 =0 \]

gelten. Diese quadratische Gleichung hat zwei Lösungen, nämlich

\[\lambda_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2} \right)^2 - q} = -\delta \pm \sqrt{\delta^2 - \omega_0^2}\]

mit \(p = 2 \delta\) und \(q = \omega_0^2 = \sqrt{\frac{k}{m}}\).

Die allgemeine Lösung der Differentialgleichung ist die Summe aller möglichen Lösungen. Damit ist

(4.2)\[x(t) = A_1 e^{\lambda_1 t}+ A_2 e^{\lambda_2 t}= A_1 e^{\left( -\delta + \sqrt{\delta^2 - \omega_0^2} \right) t}+ A_2 e^{\left( -\delta - \sqrt{\delta^2 - \omega_0^2}\right) t}\]

Nun muss eine Fallunterscheidung durchgeführt werden, da es einen Unterschied macht, ob der Exponent der e-Funktion imaginär ist, oder reell. Ist der Exponent imaginär, liegt eine Schwingung vor, beim reellen Exponenten jedoch nicht.

4.1. Schwache Dämpfung

Ist die Dämpfung schwach, so ist \(\delta < \omega_0\). Dies bedeutet aber auch, dass \(\delta^2 - \omega_0^2 <0\) ist. Dann lässt sich der Exponent der e-Funktion in (4.2) schreiben als

\(\sqrt{\delta^2 - \omega_0^2} = \sqrt{(-1)\cdot(\omega_0^2 -\delta^2)} = i\sqrt{\omega_0^2 -\delta^2}\) mit \(\omega_0^2 - \delta^2 > 0\).

Mit den Anfangsbedingungen

\[x\left(t = 0\right) = \hat{x} \text{ und } x \left( t\cdot \omega_0 = \frac{\pi}{2}\right)\]

ergibt sich für die schwach gedämpfte Schwingung die Bewegungsgleichung

\[\Rightarrow x(t) = A_1 e^{-\delta t} \cdot e^{\left( i \sqrt{\omega_0^2 - \delta^2} \right) t} + A_2 e^{-\delta t} \cdot e^{\left(- i \sqrt{\omega_0^2 - \delta^2}\right) t} = \hat{x}e^{-\delta t} \cdot \text{cos} \left( \sqrt{\delta^2 - \omega_0^2} t \right)\]

mit \(\text{cos} \left(\phi \right) = \frac{1}{2}\left(e^{i\phi} + e^{-i\phi}\right)\) und \(\hat{y} = 2 A\).

Die Bewegung des gedämpften harmonischer Oszillators ist in dem Video Abbildung 4.1 dargestellt. Die ungedämpfte Schwingung ist zum Vergleich durchscheinend dargestellt. Wie erwartet, nimmt die Amplitude der Schwingung ab, interessant ist jedoch, dass auch die Frequenz der Schwingung sich verändert.

Federpendel

Fig. 4.1 Bewegung des schwach gedämpften harmonischer Oszillators.

Die Amplitude der gedämpften Schwingung ist

\[\hat{x}_{gedämpft} = \hat{x} \cdot e^{-\delta \cdot t} \]

und die Frequenz der gedämpften Schwingung ist

\[\omega_d = \sqrt{\omega_0^2 - \delta^2} \]

und die Dämpfungskonstante ist \(\delta = \frac{\beta}{2m}\)

Und die Energie des gedämpften harmonischen Oszillators ist dann

\[E_{mech} \approx \frac{1}{2} m \omega^2 \hat{x}^2 e^{-2\delta \cdot t} =: E_{mech, \delta = 0}e^{-\frac{t}{\tau}}\]

mit \(E_{mech, \delta = 0} = \frac{1}{2}k \hat{x}^2\) und \(\tau = \frac{1}{2\delta} = \frac{m}{\beta}\).

\(\tau\) wird auch als Zeitkonstante bezeichnet.

4.1.1. Q-Faktor

Der gedämpfte Oszillator wird häufig durch einen sogenannten Gütefaktor (nach der englischen Bezeichnung quality factor auch als Q-Faktor bezeichnet) charakterisiert mit \(Q = \omega_0 \tau\).

Der Q-Faktor ist umgekehrt proportional zu dem relativen Energieverlust während einer Schwingung.

\[Q = \frac{1}{\left(\frac{\Delta E_{mech}}{E_{mech}} \right)_{Schwingungsdauer}}\]

4.1.2. Lehr’sches Dämpfungsmaß

Oft wird auch das sogenannte Lehr’sches Dämpfungsmaß angegeben, es ist definiert als

\[D = \frac{\delta}{\omega_0}\]

4.2. Aperiodischer Grenzfall

Gleichung (4.2) erreicht einen Spezialfall, wenn \(\delta = \omega_0\) ist. Dann wird die Lösung der Differentialgleichung zu

\[x(t) = A_1 e^{\left( -\delta \right) t}\]

und damit mir den Anfangsbedingungen

\[x\left(t = 0\right) = \hat{x} \text{ und } x \left( t\cdot \omega_0 = \frac{\pi}{2}\right)\]

zu

\[x(t) = \hat{x}e^{-\delta t}\]

In diesem Fall schwingt das Pendel nicht mehr, sondern kehrt in minimaler Zeit zur Ruhelage zurück.

Im aperiodischen Grenzfall gilt

\[\frac{k}{m} - \left(\frac{\beta}{2m}\right)^2=0 \Leftrightarrow \left(\frac{\beta}{2m}\right)^2 = \frac{k}{m} \Leftrightarrow \beta = 2m \sqrt{\frac{k}{m}}=2 \sqrt{km}\]

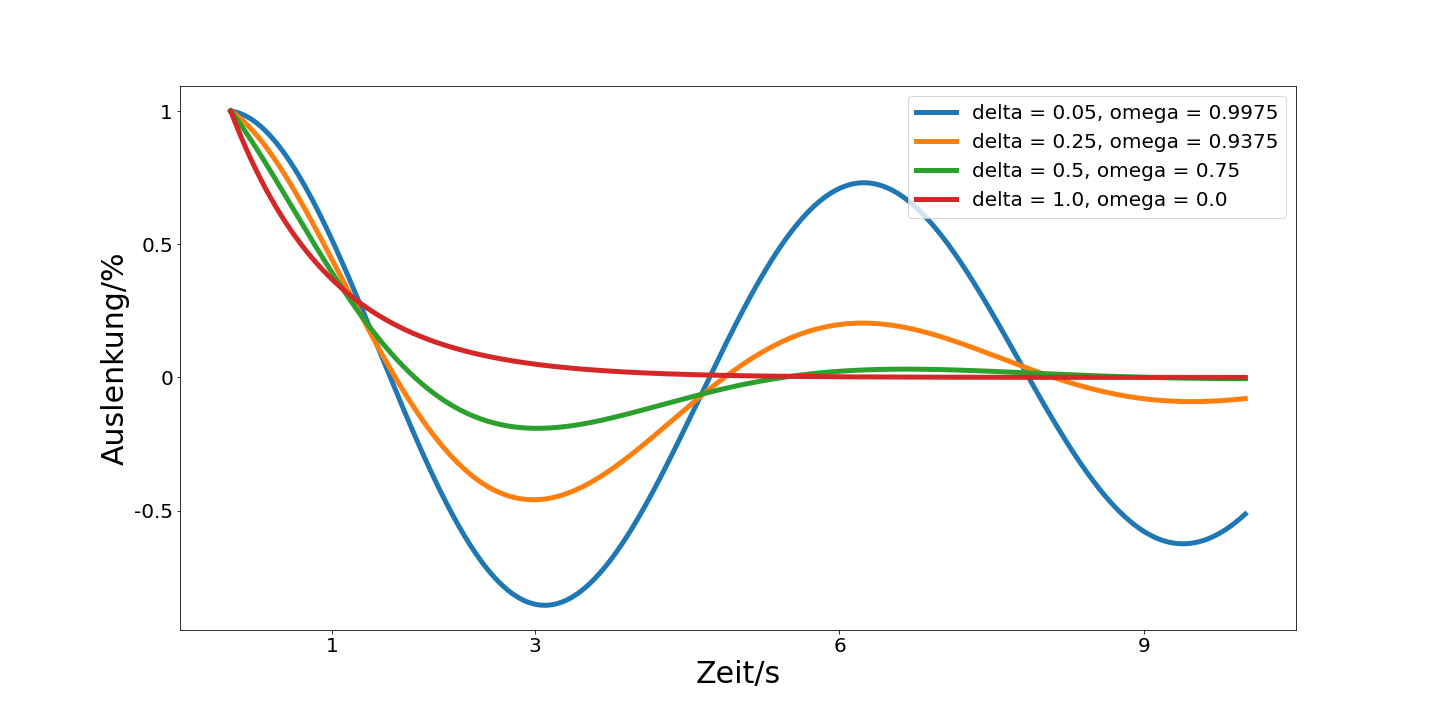
Fig. 4.2 Übergang der gedämpften Schwingung zum Kriechfall.

4.3. Starke Dämpfung

Wenn die Dämpfung noch stärker wird, wird die Bewegungsgleichung zu

\[\Rightarrow x(t) = \hat{x}e^{-\delta t} \cdot \left(e^{\sqrt{\delta^2 - \omega_0^2 } t} + e^{-\delta t} \cdot e^{- \sqrt{ \delta^2 - \omega_0^2} t} \right)\]

Federpendel

Fig. 4.3 Starke Dämpfung im Vergleich zum aperiodischen Grenzfall.

Durch den Einsatz eine genügend starken Dämpfung ist es also möglich, eine Schwingung derart stark zu Dämpfen, das kein Schwingvorgang mehr zustandekommt. Dies wird beispielsweise bei Stoßdämpfern genutzt.

Eine schöne Visualisierung von gedämpften Schwingungen ist hier zu finden.