6. Dopplereffekt#
Bislang wurden Wellen betrachtet, die von einer sich in Ruhe befindenden Quelle ausgestrahlt werden und sich von da aus ausbreiten. Bewegt sich diese Quelle jedoch, überlagen sich die Quellenbewegung und die Wellenausbreitung. Dieser Effekt wird als Dopplereffekt bezeichnet.
Hierbei gilt
Wenn sich eine Wellenquelle und ein Empfänger relativ zueinander bewegen, ist die empfangene Frequenz nicht dieselbe wie die Frequenz der Quelle.
Bewegen sie sich aufeinander zu, ist die empfangene Frequenz größer als die Frequenz der Quelle
wenn sie sich voneinander entfernen, ist die empfangene Frequenz kleiner.
Bei Schallwellen kann man den Dopplereffekt hören. Bekannte Effekte sind beispielsweise die Tonhöhenverschiebung im Motorengeräusch eines vorbeifahrenden Autos oder auch die Änderung der Tonhöhe beim Sirenengeräusch eines Polizeiwagens.
Da Schallwellen sich immer in einem Medium ausbreiten, können alle Bewegungen relativ zu diesem (ruhenden) Medium betrachtet werden. Die folgenden Betrachtungen gelten in dieser einfachen Form nur dann, wenn die Schallgeschwindigkeit im Medium viel kleiner als Lichtgeschwindigkeit ist \(v << c\).
6.1. Bewegte Quelle, ruhender Empfänger#
Wenn Quelle und Empfänger in Ruhe sind, erreichen die Wellenberge den Empfänger mit der Frequenz \(f_E = \frac{v}{\lambda_E}\). Dabei ist v die Schallgeschwindigkeit (siehe Abbildung 3.8). Wenn beide ruhen, ist die Frequenz bei Quelle und Empfänger gleich, es gilt \(\lambda_E = \lambda_Q\).
Fig. 6.4 Wellenausbreitung bei ruhender Quelle und ruhendem Empfänger#
Die Zeitdifferenz, mit der zwei Wellenberge die Quelle verlassen, ist \(T_Q = \frac{1}{f_Q}\). Wenn die Quelle sich mit \(v_Q\) auf den Empfänger zubewegt, verkürzt sich die scheinbare Wellenlänge durch die Geschwindigkeit der Quelle (siehe Abbildung 6.5).
Fig. 6.5 Wellenausbreitung bei bewegter Quelle und ruhendem Empfänger#
Die Wellenlänge beim Empfänger ist dann
Die Frequenz an der Quelle ist \(f_Q = \frac{1}{T_Q} = \frac{v}{\lambda_Q}\)
Die Frequenz, mit der die Wellenberge beim Empfänger ankommen ist
Dies bedeutet, Frequenz wird höher und auch der Ton wird höher.
Fig. 6.6 Wellenausbreitung bei bewegter Quelle und ruhendem Empfänger#
Wenn die Quelle sich mit \(v_Q\) vom Empfänger wegbewegt (siehe Abbildung 6.6), verlängert sich die scheinbare Wellenlänge durch die Geschwindigkeit der Quelle
Dann ist die Frequenz, mit der die Wellenberge beim Empfänger ankommen
Dies bedeutet, Frequenz wird niedriger und auch der Ton wird niedriger.
6.2. Ruhende Quelle, Bewegter Empfänger#
Ebenfalls verändert sich die beim Empfänger wahrgenommene Frequenz, wenn die Quelle ruht, aber der Empfänger sich bewegt. In diesem Fall bewegt sich der Empfänger bewegt an Wellenbergen vorbei (siehe Abbildung 6.7).
Fig. 6.7 Wellenausbreitung bei ruhender Quelle und bewegtem Empfänger#
Sei \(T_E\) die Zeit zwischen zwei beim bewegten Empfänger ankommenden Wellenbergen. Dann hat jeder Wellenberg in der Zeit \(T_E\) sich um die Strecke \(v \cdot T_E\) ausgebreitet. Der Empfänger hat in der Zeit die Strecke \(v_E \cdot T_E\) zurückgelegt. Damit setzt sich eine Wellenlänge aus den beiden zurückgelegten Strecken
Fig. 6.8 Wellenausbreitung bei ruhender Quelle und bewegtem Empfänger#
Die vom Empfänger wahrgenommene Frequenz ist also
Wenn sich der Empfänger vom Sender wegbewegt gilt
6.3. Zusammenfassung#
Ruht der Empfänger, gilt
Ruht die Quelle, gilt
Beide Gleichungen lassen sich kombinieren zu
\(\Longrightarrow\) Die Frequenz nimmt zu, wenn Quelle und Empfänger sich aufeinander zubewegen
\(\Longrightarrow\) Die Frequenz nimmt ab, wenn Quelle und Empfänger sich voneinander wegbewegen
6.4. Stoßwellen und Machzahl#
Wenn die Quelle sich mit einer größeren Geschwindigkeit als die Schallgeschwindigkeit bewegt (\(v_Q > v\) \(\longrightarrow\))können sich keine Wellen vor der Quelle ausbreiten, sondern die Wellen häufen sich hinter der Quelle an, und deren Wellenfronten erzeugen eine Stoßwelle (siehe Abbildung 6.9). Es entsteht ein Überschallknall.
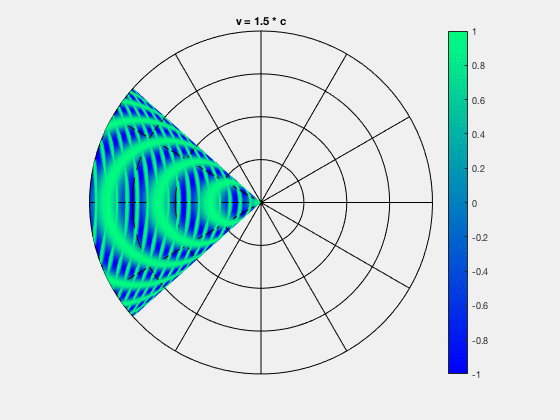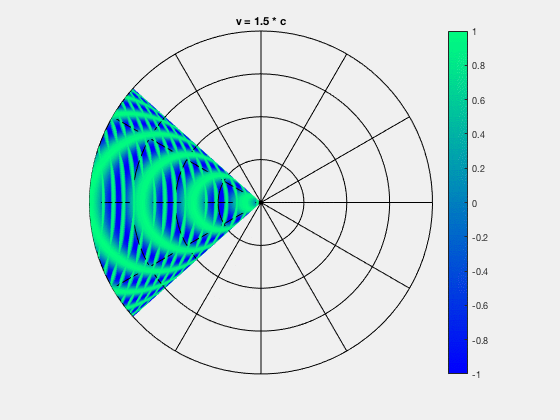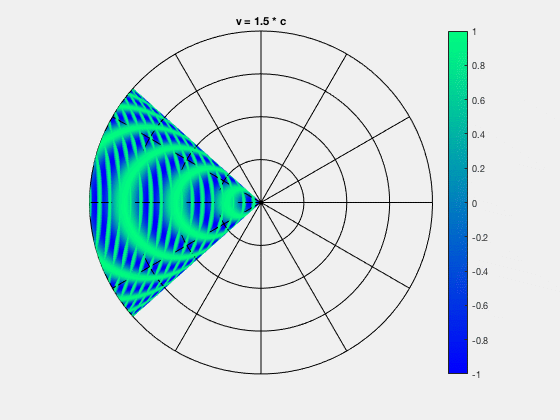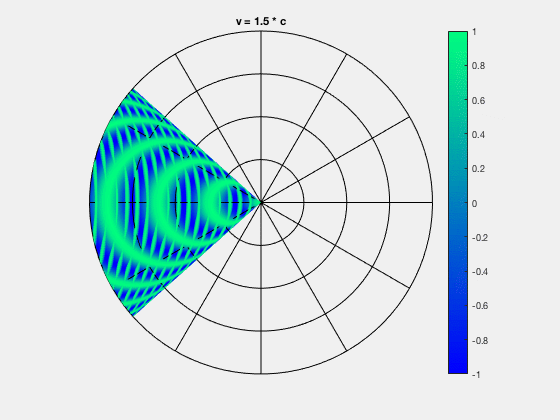
Fig. 6.9 Mach-Kegel, Von Funkmich008 - Eigenes Werk, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=59297403#
Der durch die zusammengeschobenen Wellenfronten entstehende Kegel wird auch als Mach-Kegel bezeichnet. Der Öffnungswinkel dieses Mach-Kegels kann berechnet werden durch
Je schneller sich die Quelle bewegt, desto kleiner ist der Öffnungswinkel des Mach-Kegels.
Zur Beschreibung der Geschwindigkeit im Vergleich zur Schallgeschwindigkeit wird oft die Mach-Zahl angegeben. Die Mach-Zahl ist eine dimensionslose Größe. Es gilt
wobei \(v\) die Schallgeschwindigkeit ist.
Die entstehende Stoßwelle kann machmal sogar sichtbar sein, wie auf zu Abbildung 6.10) erkennen ist.

Fig. 6.10 Ueberschallknall, Von Ensign John Gay, U.S. Navy - Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=3890362#
6.5. Relativistischer Doppler-Effekt#
Die oben betrachteten Näherungen gelten nur für Geschwindigkeiten \(v \ll c\). Für Schallwellen ist diese Näherung realistisch. Für Licht und elektromagnetische Wellen (diese sind Transversalwellen) gilt die Näherung nicht, da hier \(v = c\) ist.
Licht und andere elektromagnetische Wellen, benötigen kein Medium, um sich auszubreiten. Es kann daher auch nicht, wie beim Schall, das ruhende Medium als Bezugspunkt gewählt werden. Wichtig ist daher nur die Relativbewegung von Quelle und Empfänger zueinander.
Bei Geschwindigkeiten, die nicht klein gegenüber der Lichtgeschwindigkeit sind, treten relativistische Effekte auf (Berücksichtigung der speziellen Relativitätstheorie notwendig)
Nach der speziellen Relativitätstheorie messen alle möglichen Beobachter dieselbe Lichtgeschwindigkeit \(c\).
Für Licht und andere elektromagnetische Wellen gilt für die Frequenz, die der Empfänger misst (ohne Herleitung):
Bei Entfernung von Quelle und Empfänger ist daher
\(f_E < f_Q \longrightarrow \) Rotverschiebung
Bei Annäherung von Quelle und Empfänger ist
\(f_E > f_Q \longrightarrow \) Blauverschiebung
Die Formel (6.1) kann auch geschrieben werden als
Für \(\frac{v_{rel}}{c} \ll 1\) kann die Wurzel in einer Taylorreihe entwickelt werden. Nimmt man alle Terme bis zur Ordnung \(\left( \frac{v_{rel}}{c}\right)^1\) mit, ergibt sich näherungsweise
oder auch
