10. Stehende Wellen#
Zwei gegenläufige Wellen erzeugen eine stehende Welle, wenn sie einen Phasenunterschied von \(\delta = \frac{\pi}{2}\) haben. Eine stehende Welle, ist eine Welle, deren Auslenkung an bestimmten Stellen immer bei Null verbleibt (siehe Abbildung 10.1).
Fig. 10.1 Überlagerung zweier gegenläufiger Wellen zu einer stehenden Welle. Die Summe der beiden gegenläufigen Wellen ist die stehende Welle (Klick für Start des Videos).#
Die Punkte, an denen die Auslenkung immer \(=0\) bleibt, werden als Schwingungsknoten bezeichnet. Die Punkte, an denen die Auslenkungen zwischen den beiden Maxima hin- und her schwankt, werden Schwingungsbäuche genannt.
10.1. Stehende Welle auf einer beidseitig eingespannten Saite#
Zunächst wird zum weiteren Verständnis von stehenden Wellen eine beidseitig eingespannte Saite (wie beispielsweise eine Gitarrensaite) betrachtet.
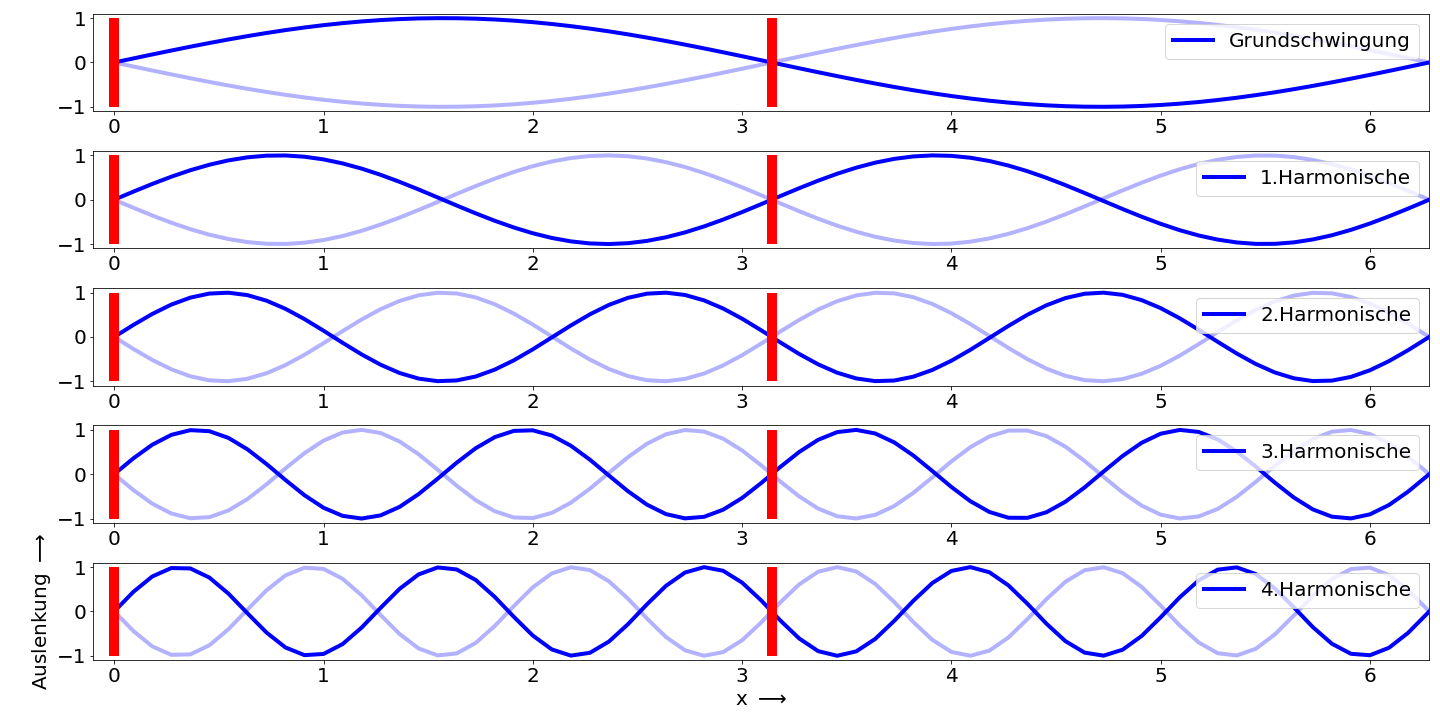
Fig. 10.2 Stehende Welle auf einer beidseitig eingespannten Saite. Die roten Balken markieren die Stellen an denen die Saite eingespannt ist, die Wellen außerhalb der roten Balken dienen nur der Illustration der Gesamtwelle.#
Die Welle wird durch Auslenkung der Saite initiiert und breitet sich auf der Saite aus. An den fest eingespannten Enden wird die Welle reflektiert und läuft als gegenläufige Welle auf der Saite zurück. Durch Überlagerung der Welle mit der rückläufigen Welle entsteht so eine stehende Welle.
Da an den Enden die Saite fest eingespannt ist, ist die Auslenkgung an den Enden \(=0\), hier befinden sich also Schwingungsknoten. Damit eine Welle als stehende Welle auf der Saite entstehen kann, muss die halbe Wellenlänge der stehenden Welle gleich der Länge der Saite sein oder ein ganzzahliges Vielfaches der halben Wellenlänge entspricht der Länge dieser Saite; es gilt
\(l = n \cdot \frac{\lambda_n}{2}\) mit \(n = 1,2,3,...\)
Dies ist in Abbildung 10.2 dargestellt. Die Schwingung, bei der die halbe Wellenlänge der Gitarrensaitenlänge entspricht, wird als Grundschwingung bezeichnet. Die Wellen mit einer geringeren Wellenlänge werden als Harmonische bezeichnet.
Aus der Bedingung \(l = n \cdot \frac{\lambda_n}{2} \Leftrightarrow \lambda_n = \frac{2 \cdot l}{n}\) wird mit \(v_{ph} = \lambda f \Rightarrow f_n = \frac{v_{ph}}{\lambda_n}\)
Damit sind die Resonanzfrequenzen einer beidseitig eingespannten Saite
mit \(n = 1,2,3,...\)
10.2. Stehende Welle mit einem offenen Ende#
Bei der Grundschwingung einer einseitig eingespannten Saite mit einem losen Ende befindet sich ein Knoten am festen Ende (roter Balken in Abbildung 10.3) und ein Bauch am losen Ende (oranger Balken in Abbildung 10.3). Da die Entfernung von einem Knoten zum benachbarten Bauch gerade ein Viertel der Wellenlänge ausmacht, entspricht bei der Grundschwingung die Saitenlänge gerade \(l = \frac{\lambda}{4}\) (siehe Abbildung 10.3).
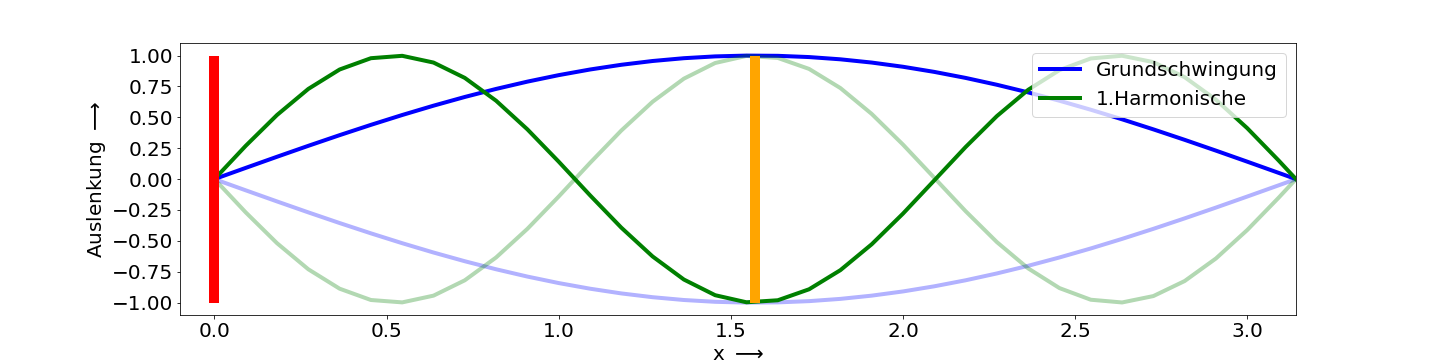
Fig. 10.3 Stehende Welle auf einer einseitig eingespannten Saite. Der rote Balken markiert die fest eingespannte Seite der Saite. Der orangene Balken zeigt das lose Ende. Die Wellen außerhalb der Balken dienen nur der Illustration der Gesamtwelle.#
Hier gilt entsprechen für die Resonanzfrequenzen der einseitig eingespannten Saite
mit \(n = 1,3,5,...\) (\(n\) ist eine ungerade ganze Zahl).
