8. Überlagerung von Wellen

Wenn Wellen aufeinandertreffen, überlagern sich diese. Dabei gilt das Superpositionsprinzip

8.1. Superpositionsprinzip

Wellen durchdringen einander, ohne sich in ihrer Ausbreitung zu stören. Wenn zwei oder mehr Wellen sich überlagern, ergibt sich die resultierende Welle als algebraische Summe der einzelnen Auslenkungen.

\[y_{ges}(t,x) = C_1 \cdot y_1(t,x) + C_2 \cdot y_2(t,x) \]

Wenn zwei Wellen eine Wellengleichung erfüllen, dann erfüllt auch ihre algebraische Summe dieselbe Wellengleichung. Die Überlagerung von Wellen gleicher Frequenz bezeichnet man als Interferenz

\[\frac{\partial^2y_{ges}(t,x)}{\partial x^2} = \frac{1}{v^2}\frac{\partial^2y_{ges}(t,x)}{\partial t^2}\]

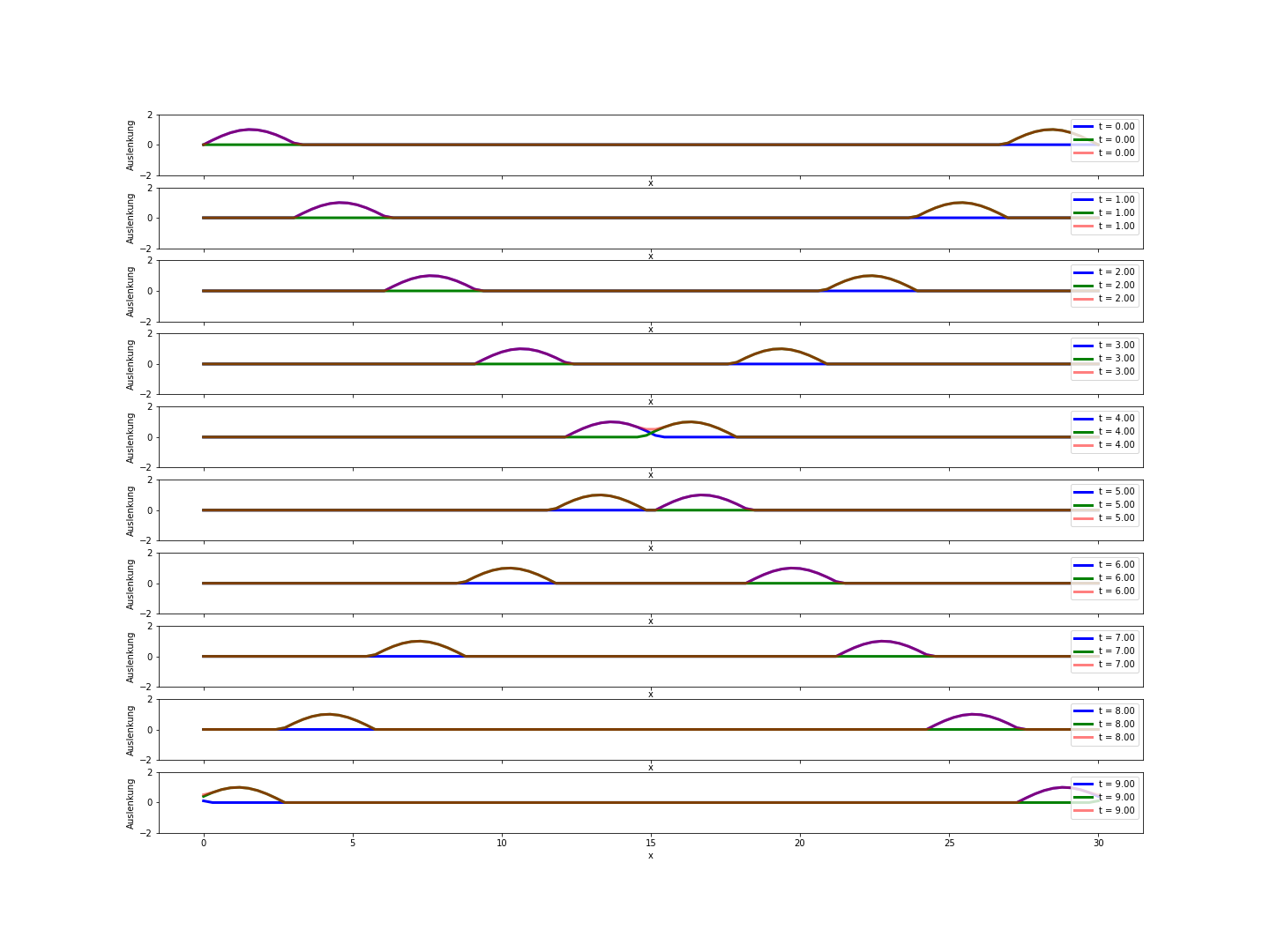
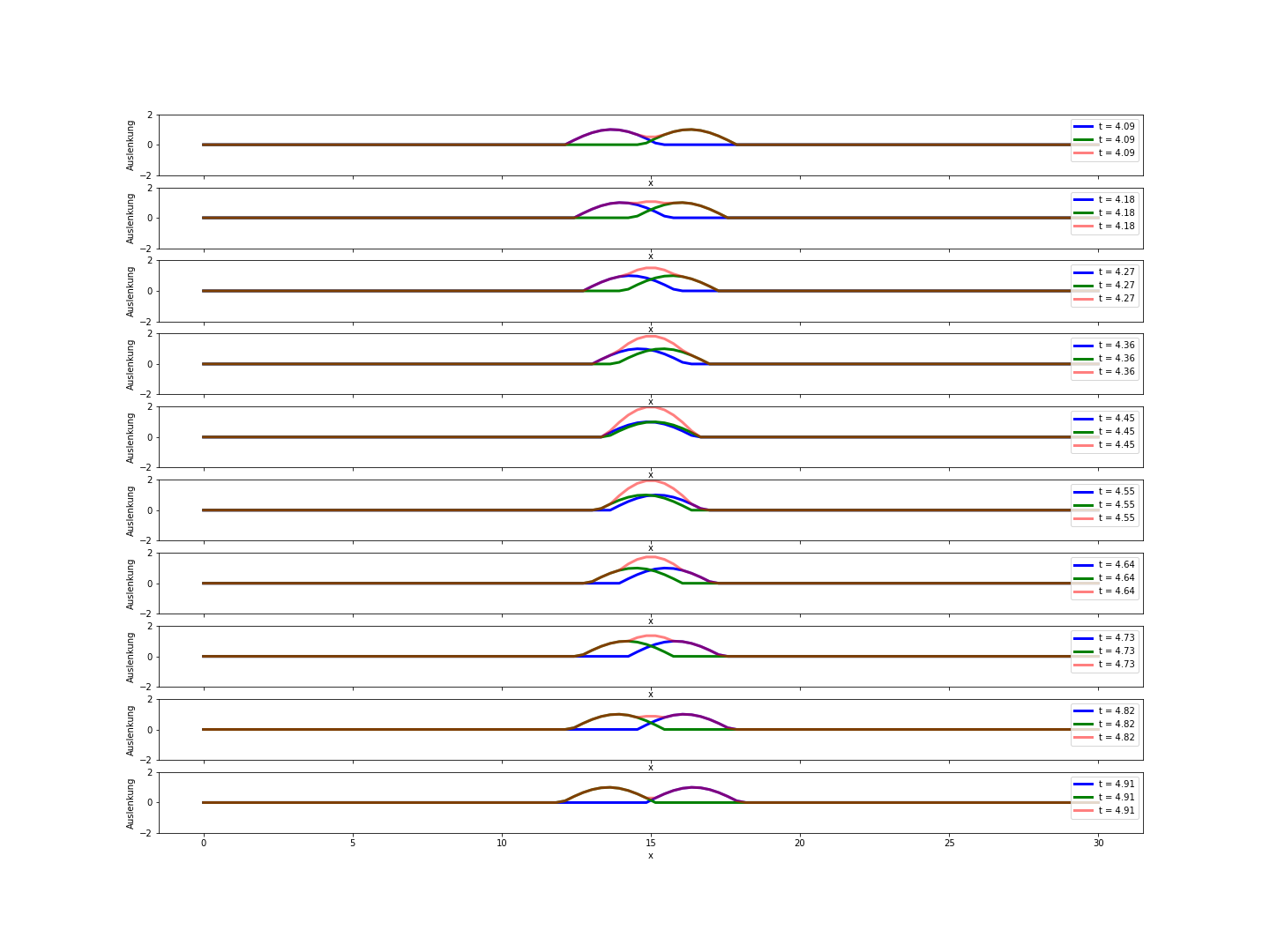
Fig. 8.1 Treffen Wellenzüge aufeinander, entsteht während der Zeit der Begegnung eine Interferenz. Von Snaily, Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=3269307

Daraus ergeben sich folgende Spezialfälle:

8.2. Auslöschung

Treffen zwei Wellen aufeinander, deren Phase gleich und deren Amplituden gegensätzlich ist, so löschen sich diese beiden Wellen aus. Dies ist in Abbildung 8.2 dargestellt. Dies bedeutet, dass es möglich ist eine Welle auszulöschen, indem eine gegensätzliche Welle überlagert wird. Dieses Prinzip wird beispielsweise bei noise cancelling Kopfhörern verwendet. Dieses Prinzip gilt für alle Wellen, also auch für Licht und andere elektromagnetische Wellen.

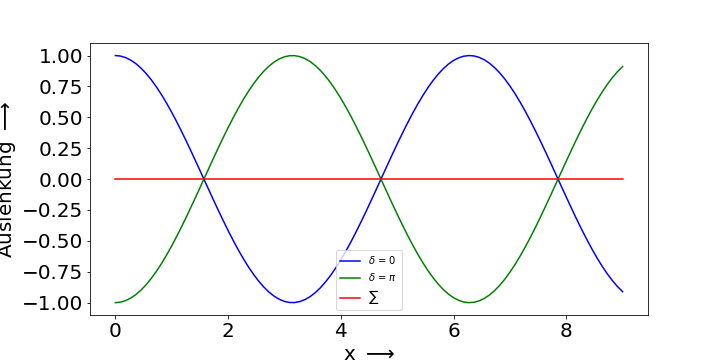
Fig. 8.2 Auslöschung zweier Wellen durch Überlagerung.

8.3. Verstärkung

Treffen zwei Wellen aufeinander, deren Phase gleich und deren Amplitude das gleiche Vorzeichen hat, so addieren sich die beiden Amplituden zur neuen Gesamtamplitude. Die beiden Wellen verstärken sich.