5. Newton’sche Ringe

Fig. 5.4 Newtonsche Ringe zwischen einer schwach gekrümmten Linse (Krümmungsradius ca. 13 m) und einer ebenen Platte, beleuchtet durch das einfarbige Licht einer Natriumdampflampe (\(\lambda = 589 \, nm\)). Quelle: Noah-Marcel Fath, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=53508832

Newtonsche Ringe sind Interferenzmuster, die durch Interferenz am Luftspalt zwischen zwei reflektierenden, nahezu parallelen Oberflächen entstehen.

Der Effekt wird genutzt, um die Qualität der Form von Linsen zu beurteilen. Die Anzahl und Symmetrie der zu beobachtenden Ringe bei Einlegen der Linse in eine Referenzform dient dabei zuweilen als Maß für die Qualität. Anhand der Ringe oder „Höhenlinien“ können auch Dickenschwankungen dünner Schichten abgeschätzt werden. Auch für die berührungsfreie Güteprüfung von Spiegeln hoher und höchster Qualität, vor allem für Spiegelteleskope, wird der Effekt genutzt.

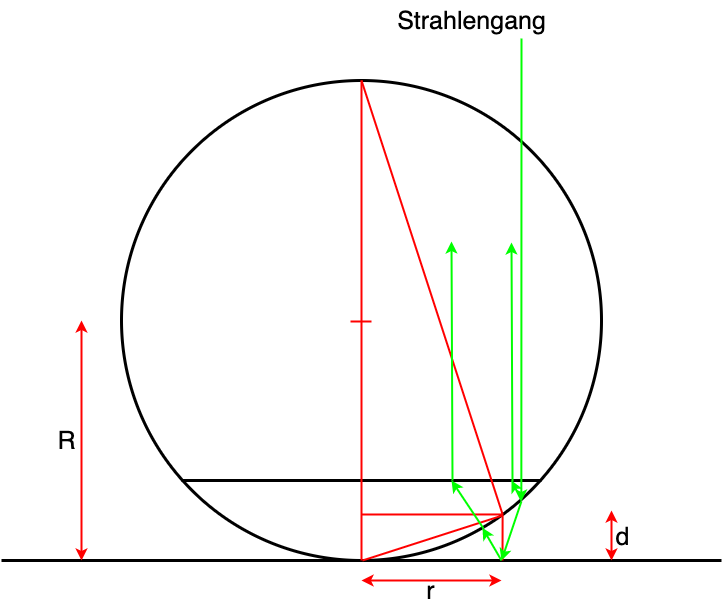
Fig. 5.5 Strahlengang bei Newtonschen Ringen

Damit ist der Gangunterschied der reflektierten Strahlen

\[ \begin{equation} \delta = 2 \cdot d + \frac{\lambda}{2} \end{equation} \]

Über den Höhensatz ergibt sich

\[r^2 = \left(2 R - d \right) d\]

mit \(R \gg d\) ist dies

(5.5)\[ \begin{equation} r^2 \approx 2 R d \Leftrightarrow d = \frac{r^2}{2R} \end{equation} \]

Dann ergibt sich konstruktive Interferenz (Maxima) bei:

\[ \begin{equation} \delta = 2 \cdot d + \frac{\lambda}{2} = n\cdot \lambda \end{equation} \]

mit \(n \in {1,2,3,...}\).

Mit Gleichung (5.5) ist

\[ \begin{equation} r^2 = nR \lambda \end{equation} \]

mit \(n \in {1,2,3,...}\)

und destruktive Interferenz (Minima) bei

\[ \begin{equation} \delta = 2 \cdot d + \frac{\lambda}{2} = \left( n - \frac{1}{2} \right) \cdot \lambda \Leftrightarrow d = n \frac{\lambda}{2} \end{equation} \]

mit \(n \in {1,2,3,...}\).

Mit Gleichung (5.5) \ ist

\[ \begin{equation} r^2 = R\lambda \left(n - \frac{1}{2} \right) \end{equation} \]

mit \(n \in {1,2,3,...}\)