5. Arbeit, Leistung und Energie

Eine Kraft, die an einer Masse angreift, bewirkt eine Bewegung. Wirkt eine Kraft \(F\) auf einen materiellen Punkt oder Körper und verschiebt ihn dabei um ein Wegelement \(\Delta s\), so hat die Kraft den Zustand des Körpers verändert. Man bezeichnet diesen Vorgang auch als Arbeit, die verrichtet wird. Arbeit ist dabei keine vektorielle, sondern eine skalare Größe. Sie wird oft mit \(W\) bezeichnet, die Einheit ist \(1 \, J = 1\) Joule \(= 1 \, Nm\).

5.1. Arbeit

Definition Die Arbeit ist das Wegintegral der Kraft (siehe Abbildung 5.1).

\(dW = \vec{F}\cdot d\vec{s}\)

\(W_{12} = \int_1^2 dW = \int_{s_1}^{s_2} \vec{F} \cdot d\vec{s}\)

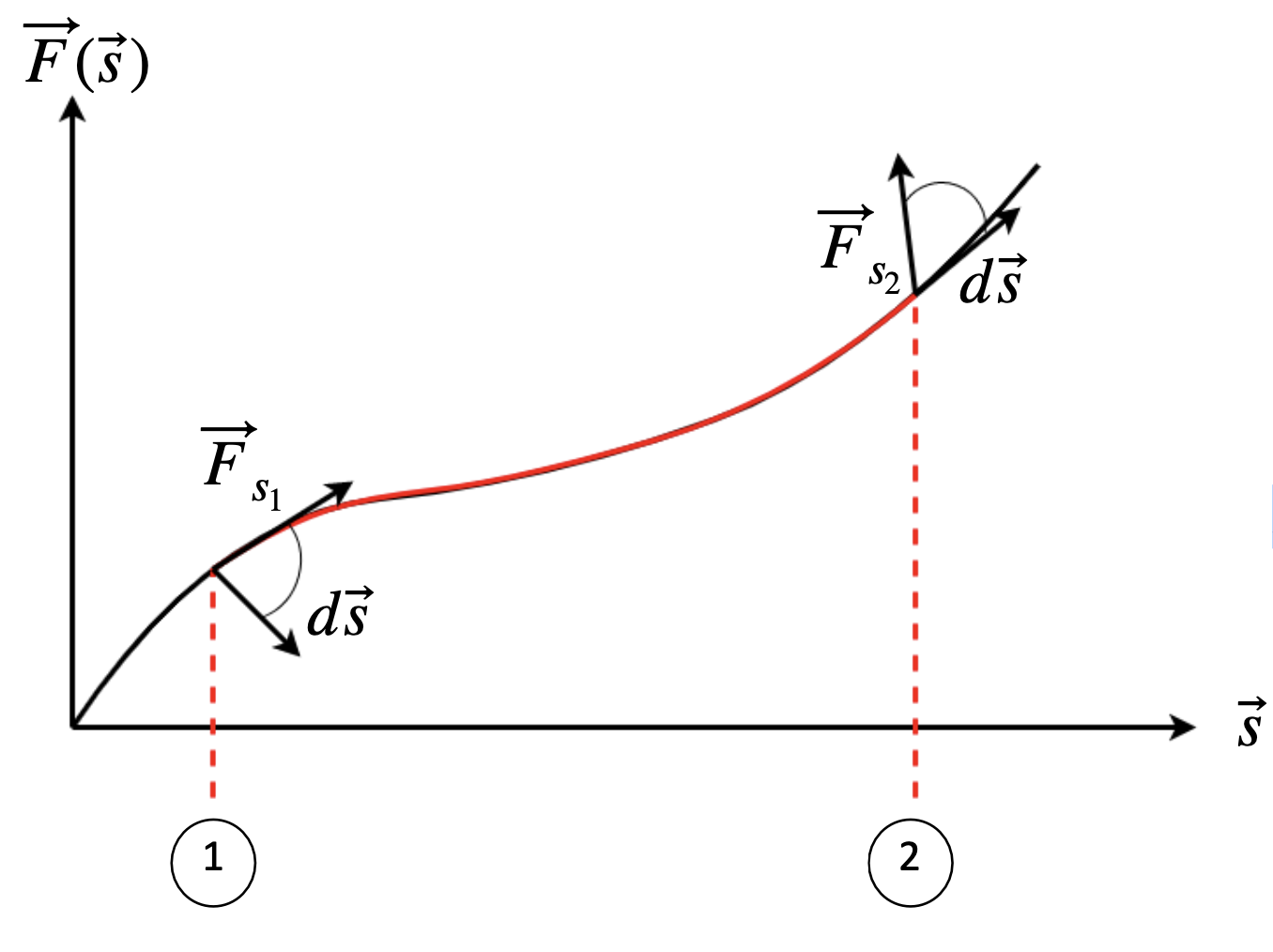
Fig. 5.1 Arbeit als Wegintegral der Kraft.

Ist die Kraft, die entlang des Wegelementes wirkt, konstant, so lässt sich schreiben

\(\Delta W = \vec{F} \cdot \Delta \vec{s}\)

Das Skalarprodukt \(\vec{F} \cdot \Delta \vec{s}\) bewirkt, dass nur diejenige Kraftkomponente beiträgt, die parallel zum zurückgelegten Weg wirkt (siehe Abbildung 5.2).

\(\Delta W = \left|\vec{F} \right| \cdot \left| \Delta \vec{s} \right| \cdot cos \left( \angle \left(\vec{F}, \Delta \vec{s}\right) \right)\)

Der \(cos\left( \angle \left(\vec{F}, \Delta \vec{s}\right) \right)\) ist =1, wenn \(\vec{F} \parallel \Delta\vec{s}\) und =0, wenn \(\vec{F} \perp \Delta\vec{s}\).

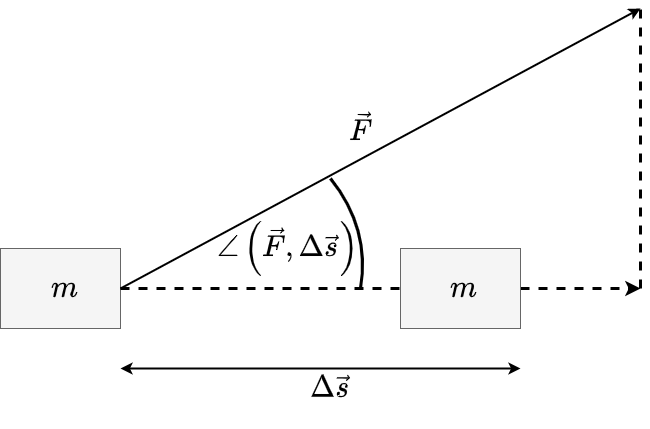
Fig. 5.2 Nur der zum Weg parallele Anteil der wirkenden Kraft verrichtet Arbeit.

5.1.1. Beispiel: Verschiebearbeit

Verschiebearbeit ist die Arbeit, die verrichtet wird, wenn ein Gegenstand durch eine konstante Kraft \(F_x\) entlang eines Weges \(x\) verschoben wird.

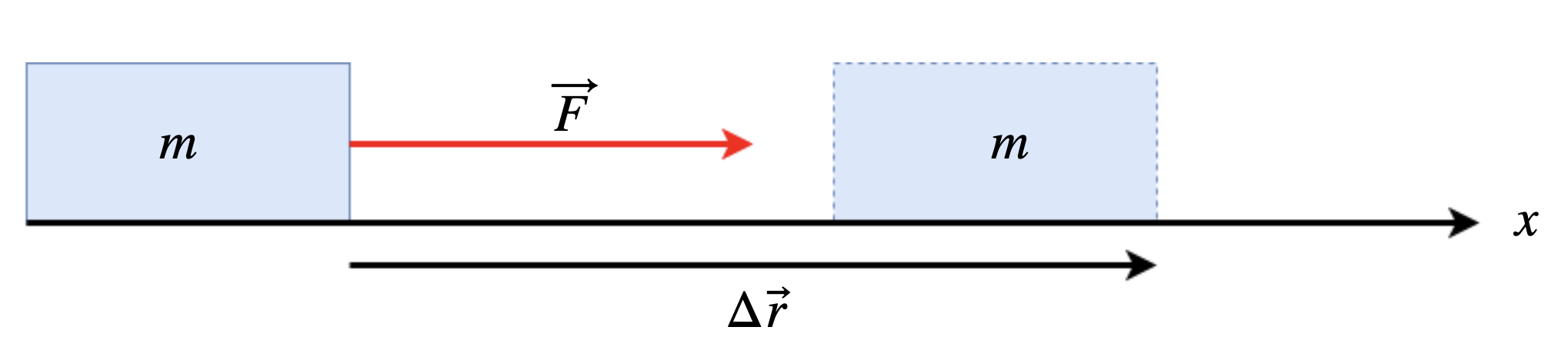
Fig. 5.3 Verschiebearbeit: Die Kraft \(\vec{F}\) bewirkt eine Verschiebung der Masse \(m\) entlang der x-Achse.

Dann gilt

\(W_{12} = \int_1^2 \vec{F}(\vec{r}) d\vec{r} = \int_{x_1}^{x_2} F_x dx = F_x \int_{x_1}^{x_2} dx = F_x \left( x_2 - x_1 \right) = F_x \Delta x\)

5.1.2. Beispiel: Hubarbeit

Hubarbeit ist die Arbeit, die verrichtet wird, wenn ein Gegenstand um eine Höhe \(h\) gegen die Gewichtskraft \(m\cdot g\) angehoben wird.

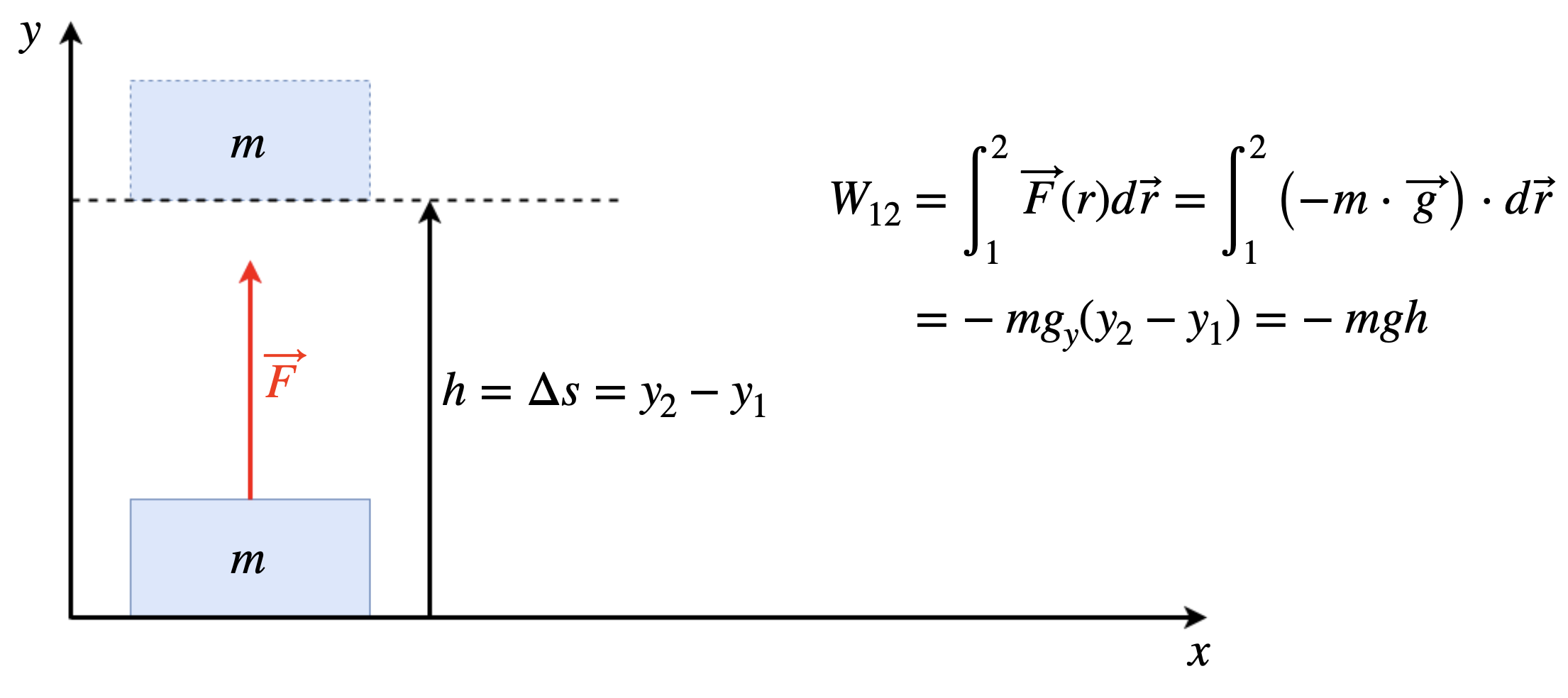
Fig. 5.4 Hubarbeit: Die Kraft \(\vec{F}\) bewirkt eine Anhebung der Masse \(m\) um die Höhe \(h\).

Dann gilt

\(W_{12} = \int_1^2 \vec{F}(r) d \vec{r} = \int_1^2 \left( - m \cdot \vec{g} \right) \cdot d \vec{r} = - m g_y (y_2 - y_1) = - m g h\)

5.1.3. Beispiel: Beschleunigungsarbeit

Beschleunigungsarbeit wird verrichtet, wenn ein Gegenstand durch eine wirkende Kraft von einer Geschwindigkeit \(v_1\) auf eine Geschwindigkeit \(v_2\) beschleunigt wird.

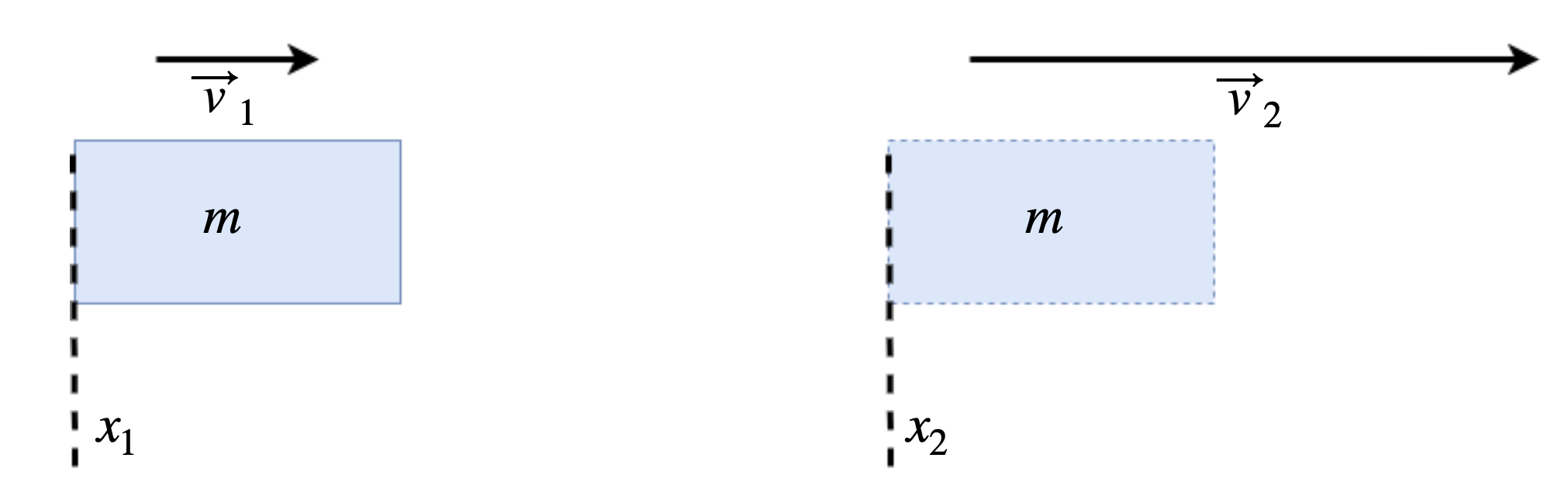
Fig. 5.5 Beschleunigungsarbeit: Die Kraft \(\vec{F}\) bewirkt eine Beschleunigung der Masse \(m\).

Dann gilt

\(W_{kin} = \int_1^2 F(x) dx = \int_1^2 m \cdot a \,dx = m\int_1^2 \frac{d v(t) }{dt} dx\)

Substitution \(v = \frac{dx}{dt} \Leftrightarrow dx = v \cdot dt\)

\(\Rightarrow W_{kin} = m \int_1^2 \frac{dv}{dt} v \, dt\)

Aufgrund der Kettenregel gilt: \(\frac{d}{dt} f\left( g (t) \right) = \frac{\partial f}{\partial g} \frac{dg}{dt}\)

und damit gilt beispielsweise mit

\(f = \frac{1}{2} \left(v(t)\right)^2 \Rightarrow \frac{d}{dt} \left( \frac{1}{2} v^2(t) \right) = v(t) \frac{dv(t)}{dt}\)

\(\Rightarrow W_{kin} = m \int_1^2 \frac{dv}{dt} v \, dt = m \left|\frac{1}{2} \left( v(t) \right)^2 \right|_1^2 = \frac{m}{2} \left( v^2(t_2) - v^2(t_1) \right)\)

5.2. Leistung

Definition Leistung ist verrichtete Arbeit pro Zeit

Dies bedeutet, die Leistung \(P\) gibt an, wie viel Arbeit in einem bestimmten Zeitraum verrichtet wurde. Es gilt damit

\(P = \frac{dW}{dt}\)

Die Einheit der Leistung ist \([P] = 1\, \frac{J}{s} = 1 \, W = 1\) Watt.

5.2.1. Beispiel: Mechanische Leistung

Ein Wanderer wiegt \(70 \, kg\) und trägt einen \(7 \, kg\) schweren Rucksack auf einen um \(200 \, m\) höher gelegenen Gipfel eines Berges hinauf. Er benötigt hierfür \(30 \, min\). Welche Leistung bringt der Wanderer durchschnittlich auf, um den Rucksack auf den Berg zu tragen?

Hubarbeit für den Wanderer: \(\Delta W_W = m_w g h = 70 \,kg \cdot 9.81 \frac{kg\cdot m}{s^2}\cdot 200m = 137,34 \,kJ\)

Hubarbeit für den Rucksack: \(\Delta W_R = m_R g h = 7 \,kg \cdot 9.81 \frac{kg\cdot m}{s^2}\cdot 200m = 13,734 \,kJ\)

Für die Leistung gilt:

\(P = \frac{dW}{dt} \stackrel{Durchschnittswert}{=}\frac{\Delta W}{\Delta t}\)

Damit muss der Wanderer durchschnittlich die Leistung

\(\overline{P}_W = \frac{\Delta W_W}{\Delta t} = \frac{137,34 \, kJ}{30\cdot 60 s} = 76,3 \,W\)

aufbringen, um die \(200 \) Höhenmeter zu überwinden. Um den Rucksack auf den Berg zu tragen muss zusätzlich die Leistung

\(\overline{P}_R = \frac{\Delta W_W}{\Delta t} = \frac{13,734 \, kJ}{30\cdot 60 s} = 7,63 \,W\) aufgebracht werden.

Insgesamt ist damit die benötigte Leistung

\(\overline{P}_{Ges} = \overline{P}_W + \overline{P}_R = 83,93 \, W\)

5.2.2. Beispiel: Mechanische Leistung 2

Ein Auto fährt bei einer gesamten Fahrwiderstandskraft \(F = 1200\, N\) von eine Geschwindigkeit von \(v = 72 \frac{km}{h} = 20 \frac{m}{s}\). Berechnen Sie die mechanische Leistung, die der Motor des Autos aufbringt.

Die Fahrwiderstandskraft \(F = 1200\, N\) ist konstant, daher gilt

\(W = \int F \, ds = F\int ds \)

Die Leistung ist daher

\(P = \frac{dW}{dt} = \frac{d}{dt} F\int ds = F \int \frac{ds}{dt} = F \int dv = F \cdot v\)

Damit ist

\(P = 1200 \, N \cdot 20 \frac{m}{s} = 24 \, kW\)

5.3. Energie

Arbeit und Energie stehen in enger Beziehung. Die Energie kennzeichnet die Fähigkeit eines Körpers oder Systems, Arbeit zu verrichten. Arbeit ist also eine Vorgangsgröße, Energie eine Systemeigenschaft beziehungsweise Zustandsgröße. Die Einheit der Energie ist gleich der Einheit der Arbeit, also \(\left[ E \right] = 1 \, J\).

Arbeit \(\longrightarrow\) beschreibt Vorgang

Energie \(\longrightarrow\) beschreibt Zustand

Energiesatz der Mechanik:

\(\Delta E = E_{nachher} - E_{vorher} = \Delta W\)

In der klassischen Mechanik gilt der Energieerhaltungssatz:

In einem abgeschlossenen System bleibt der Energieinhalt konstant. Energie kann weder vernichtet werden noch aus nichts entstehen; sie kann sich in verschiedene Formen umwandeln oder zwischen verschiedenen Teilen des Systems ausgetauscht werden.

\(E_{ges} = E_{kin} + E_{pot} \left( + E_{diss} \right) = \text{konstant}\)

Die dissipative Energie (Reibung) wird oft als Verlustenergie bezeichnet. Dies ist falsch, da keine Energie verloren geht, allerdings wird sie in thermische Energie (mit niedriger Temperatur) umgewandelt und kann nicht mehr in kinetische oder potentielle Energie umgewandelt werden.

Der Energieerhaltungssatz ist ein oft verwendeter Satz. Es kann beispielsweise verwendet werden, um Anfangs- und Endzustände einer Bewegung in Relation zu setzen, ohne dass die genauen Bewegungsgleichungen benötigt werden.

5.3.1. Beispiel: Energieerhaltungssatz

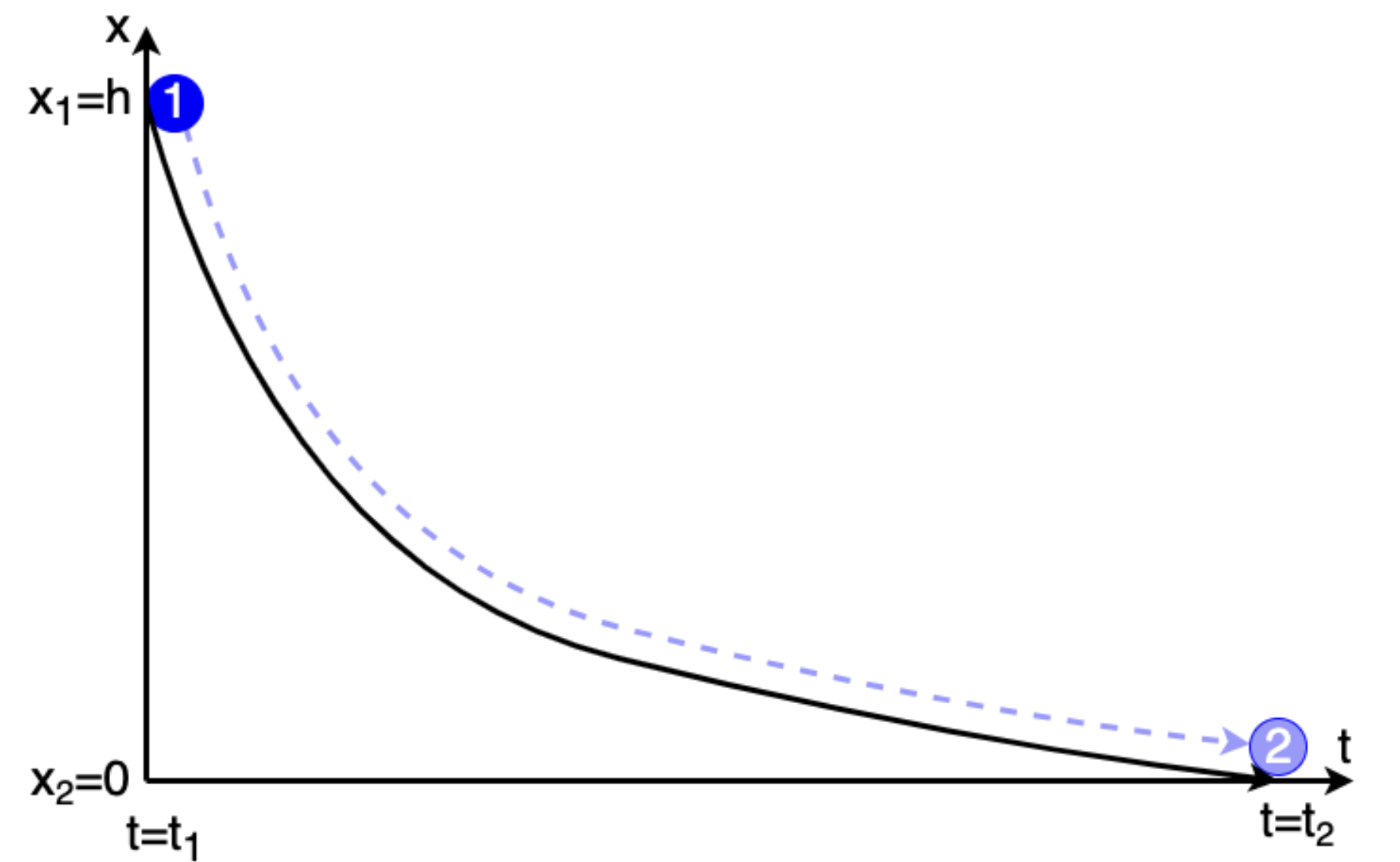
Fig. 5.6 Beispiel zur Energieerhaltung.

Für die Hubarbeit gilt (siehe beispiel-hubarbeit)

\(E_{pot}: \,\,\, W_{pot} \text{ Hubarbeit von } (1) \text{ nach } (2)\)

\(W_{pot} = W_{12} = mg \left( x_2 - x_1\right) = mgh =: E_{pot}\)

Für die Beschleunigungsarbeit gilt (siehe beispiel-beschleunigungsarbeit)

\(E_{kin} = W_{kin} = \text{ Beschleunigungs von (1) nach (2) } = \frac{m}{2} \left( v^2(t_2) - v^2(t_1) \right) = \frac{m}{2} v^2\)

mit \( v\left( t_1 \right) = 0\) und \(v \left( t_2 \right) = v(t) \).

Damit gilt für die Gesamtenergie \(E_{ges} = E_{kin} + E_{pot} = \) konstant

In (1) gilt \(v = 0 \Rightarrow E_{ges} = E_{pot}\)

In (2) gilt \(h = 0 \Rightarrow E_{ges} = E_{kin}\)

\(\Rightarrow E_{pot,1} = E_{kin,2}\)

\(\Rightarrow mgh = \frac{m}{2}v^2 \Leftrightarrow v^2 = 2 g h \Leftrightarrow \left| v\right| =\sqrt{2gh}\)

Damit lässt sich mit einfachen Mitteln die Geschwindigkeit im Punkt (2) berechnen, ohne dass die genauen Bewegungsgleichungen bekannt sind.

5.4. Energie bei Drehbewegungen

Bei der Drehbewegung eines Massenpunktes (siehe Kreisbewegungen) hat der Massenpunkt kinetische Energie

\(E_{kin} = \frac{1}{2}m \cdot v^2\)

bei der Kreisbewegung gilt

\(\omega = \frac{v}{r} \Leftrightarrow v = \omega \cdot r\)

Damit ist

\(E_{kin} = \frac{1}{2}m \cdot v^2 = \frac{1}{2}m \cdot \left( \omega \cdot r \right)^2\)