4. Temperatureffekte auf Festkörper

Beim Festkörper sind die Moleküle/Atome in einer festen Gitterstruktur eingebunden. Die Bewegungen der Moleküle/Atom besteht aus Schwingungen um ihren Ruhepunkt. Nimmt die Temperatur zu, werden diese Schwingungen größer, sodass sich der mittlere Atomabstand vergrößert. Diese Ausdehnung findet auf mikroskopischer Ebene statt, da sich aber viele mikroskopische Ausdehnungen addieren, summieren sie sich zu makroskopischen Auswirkungen.

4.1. Lineare Ausdehnung

Um diese Ausdehnung zu berechnen, wird zunächst ein 1-dimensionaler Festkörper betrachtet.

Fig. 4.25 Laengenausdehnung beim eindimensionalen Festkörper

Da es sich beim eindimensionalen Festkörper um eine Ausdehnung entlang einer Linie handelt, wird diese Ausdehnung durch den linearen Längenausdehnungskoeffizient. Dieser Längenausdehnungskoeffizient wird im Folgenden mit \(\alpha\) bezeichnet. Der Längenausdehnungskoeffizient ist stoffspezifisch und hat die Einheit \(\left[ \alpha \right] = \frac{1}{K}\)

Der (lineare) Längenausdehnungskoeffizient \(\alpha\) eines Festkörpers mit der Länge \(L\) ist definiert als

\(\alpha \cdot L = \frac{\partial L}{\partial T} \)

Im allgemeinen ist \(\alpha\) eine nichtlineare Funktion von T (siehe Abbildung 8.1) \(\Rightarrow \alpha = \alpha(T)\).

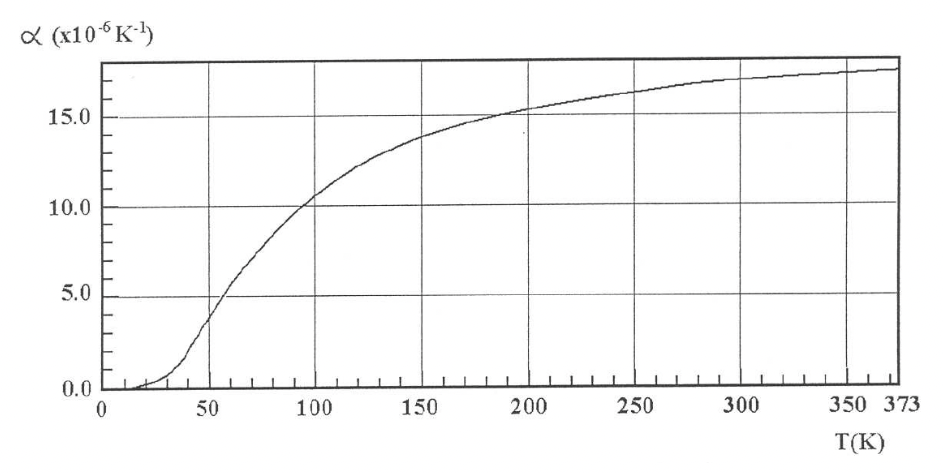
Fig. 4.26 Temperaturabhängigkeit des Längenausdehnungskoeffizient am Beispiel Kupfer. Quelle: TU Dresden

Betrachtet man nicht allzu große Temperaturänderungen, kann die Temperaturabhängigkeit des Längenausdehnungskoeffizients vernachlässigt werden. Diese Näherung gilt dann natürlich auch nur für einen Temperaturbereich. Bei Literaturangaben muss daher immer auch der referenzierte Temperaturbereich beachtet werden. Näherungsweise gilt dann für den linearen Bereich

\(\alpha \left(T \right) = \alpha \left(T_0 \right) = \textnormal{konst.}\)

Mit diesem Ansatz folgt aus

\(\alpha \cdot L = \frac{\partial L}{\partial T} \Rightarrow \Rightarrow L = L_0 \cdot e^{\alpha \cdot \Delta T}\)

Um die Anwendung der Formel zu vereinfachen, kann man beispielsweise eine Taylorentwicklung nutzen.

\(e^x = \sum_{i=0}^{\infty} \frac{x^i}{i!} \approx 1 + x + \frac{x^2}{2} + \cdots \Rightarrow L \approx L_0 \left(1 + \alpha \Delta T + \alpha^2 \frac{\Delta T^2}{2} + \cdots \right)\)

In vielen Fällen reicht es, nur Terme bis zur ersten Ordnung zu berücksichtigen. Dies bedeutet, dass dann

\(L \approx L_0 \left(1 + \alpha \Delta T \right) = L_0 + L \left(\Delta T \right) = L \left(T + \Delta T \right)\)

Bei großen Temperaturdifferenzen kann es notwendig sein mit mehreren Ausdehnungskoeffizienten zu rechnen und auch Terme \(\propto\) zu berücksichtigen.

4.1.1. Beispiel: 1 dimensionale Längenausdehnung

Zwischen den Schienen der Eisenbahn, deren Länge \(12\, m\) beträgt, bleibt ein Abstand von \(7\, mm\). Mit welchen Temperaturdifferenzen rechnen die Bautechniker, wenn der lineare Ausdehnungskoeffizient des Schienenstahls \(\alpha = 1,1 \cdot 10^{-5} \frac{1}{K}\) beträgt?

Fig. 4.27 Laengenausdehnung beim eindimensionalen Festkörper

Zwischen den Eisenbahnschienen sind \(7\, mm\) Abstand, dies bedeutet, dass sich die Schienen maximal um diese Länge ausdehnen dürfen, ohne dass sie aneinander stoßen und es zu ungewollten Spannungen kommt. Die Schienen können als eindimensional angenommen werden, da die Ausdehnung in der Länge viel größer als die Ausdehnung in Breite und Höhe sind.

\(L \left(T + \Delta T \right) = L \left(T\right) + L \left(\Delta T \right) = L_0 + L \left(\Delta T \right) = L_0 \left(1 + \alpha \Delta T \right)\)

Damit ist

\(L \left(\Delta T \right) = L_0 \left(\alpha \Delta T \right) \Leftrightarrow \Delta T = \frac{\Delta L}{L} \frac{1}{\alpha} \approx 53 ^\circ C\)

4.1.2. Beispiel: Brücken

Fig. 4.28 Laengenausdehnung bei einer Brücke

Für die in Abbildung 4.28 dargestellte Brücke gilt im Sommer

\(\Delta T = T_{Sommer} - 20 ^\circ = 20 \,K\)

\(L_{Sommer} = 200 \, m \left(1 + 11 \cdot 10^{-6}\cdot 20 \right) \)

und im Winter

\(\Delta T = T_{Winter} - 20 ^\circ = - 50 \,K\)

\(L_{Winter} = 200 \, m \left(1 - 11 \cdot 10^{-6}\cdot 50 \right) \)

Damit ist der Längenunterschied zwischen Sommer und Winter

\(\Rightarrow L_{Sommer} - L_{Winter} \approx 15 \, cm \)

Die Golden Gate Bridge mit einer Länge von \(2.7 \, km\) hat damit eine Längendifferenz von \(\Delta L = 2700 \, m \cdot \left(1 + \alpha \cdot 70 \, K \right) \approx 2 \, m\).

4.1.3. Beispiel: Kohlekessel

Das Kohlekraftwerk Weisweiler besteht aus mehreren Blöcken. Einer der größeren Blöcke hat eine Leistung von \(600 \, MW\). Der Kessel eines 600-MW-Blocks hat einen Querschnitt von etwa 20 mal 20 Metern, eine Höhe von etwa 125 Metern. Die Temperatur erreicht im Kessel etwa 1.000 Grad.

Um die Temperaturausdehnung des Kohlekessels abzuschätzen muss ein großer Temperaturbereich von \(20^\circ\) bis \(1000^\circ\) durchlaufen werden. Hier ist die Näherung durch einen linearen Längenausdehnungskoeffizienten nur sehr ungenau. Sinnvoll ist es, die Ausdehnung in 2 Temperaturbereiche aufzuteilen, die dann jeweils nacheinander betrachtet werden.

Für Stahl gilt abschätzungsweise

\(\bar{\alpha}_{0-200 ^\circ C} =: \bar{\alpha}_1 \approx 13 \cdot 10^{-6} K^{-1}\)

\(\bar{\alpha}_{200-1000 ^\circ C} =: \bar{\alpha}_2 \approx 19 \cdot 10^{-6} K^{-1}\)

Damit ist mit \(L(0^\circ C) = 125 \, m\)

\(\Rightarrow L_1 = L(200^\circ C) = L_0 \left(1 +\bar{\alpha}_1 \cdot \Delta T_1 \right) = 125 \, m \left(1 + 13 \cdot 10^{-6} K^{-1} \cdot 200 \cdot K^{-1}\right) \approx 125.33 \, m\)

\(\Rightarrow L_2 = L(1000^\circ C) = L_1 \left(1 +\bar{\alpha}_2 \cdot \Delta T_2\right) = L_1\left(1 + 19 \cdot 10^{-6} K^{-1} \cdot 800 \cdot K^{-1}\right) \approx 127.23 \, m\)

4.1.4. Anwendung: Bimetallstreifen

Eine einfache Anwendung ist der Bimetallstreifen. Hier werden 2 Metallstreifen aus unterschiedlichen Metallen aufeinandergeklebt. Aufgrund der unterschiedlichen Längenausdehnung bei Temperaturänderung verändert sich die Länge der einzelnen Metalle verschieden. Dies führt zu einer Biegung des Bimetall. Auf diese Weise lassen sich Thermometer oder temeraturabhängige Schalter realisieren.

Fig. 4.29 Prinzip eines Bimetall

4.1.5. Beispiel: Bimetallstreifen

Nach welcher Seite biegt sich ein Bimetallstreifen aus Eisen und Aluminium bei Temperaturerhöhung?

Der Längenausdehnungskoeffizient von Eisen ist \(\alpha_{Eisen} = 11.8 \cdot 10^{-6} \, \frac{1}{K}\)

Der Längenausdehnungskoeffizient von Aluminium ist \(\alpha_{Alu} = 23.1 \cdot 10^{-6} \, \frac{1}{K}\)

\(\Rightarrow\) Die Aluminiumseite dehnt sich stärker aus \(\Rightarrow\) Das Bimetall biegt sich in Richtung Eisen.

4.2. Räumliche Ausdehnung

In 3D kann statt der Längenausdehnung \(\alpha\) auch die Volumenausdehnung \(\gamma\) angegeben werden. Für isotrope Stoffe gilt

\(V + \Delta V = L_1\left(1 + \alpha \Delta T \right) \cdot L_2\left(1 + \alpha \Delta T \right) \cdot L_3\left(1 + \alpha \Delta T \right) = L_1 \cdot L_2 \cdot L_3 \left(1 + \alpha \Delta T \right)^3\)

\(= V\left(1 + 3 \alpha \Delta T + \text{Terme}\propto \alpha^2 + \cdots \right) \Rightarrow V + \Delta V \approx V \left( 1 + 3 \alpha \Delta T \right)\)

Dabei ist der Volumenausdehnungskoeffizient \(\gamma = 3\alpha\).

In ähnlicher Weise gilt für die Flächenausdehnung von zweidimensionalen Objekten

\(A + \Delta A \approx A \left( 1 + 2 \alpha \Delta T \right)\)

Einige Stoffe sind anisotrop, dies bedeutet, dass der Ausdehnungskoeffizient richtungsabhängig ist. Ein bekanntes Beispiel für einen anisotropen Stoff ist Holz,Die Ausdehnung quer zur Faser ist etwa zehnmal größer als längs der Faser.

Eine Übersicht über verschiedene Ausdehnungskoeffizienten ist hier zu finden.

4.2.1. Beispiel: 3 dimensionale Längenausdehnung

Herr Müller hat sich einen Kaffee gekocht. Herr Müller trinkt gerne Kaffee, aber immer mit Milch. Doch heute füllt er seine Tasse aus Versehen randvoll mit Kaffee (\(\gamma_K = 0,00018 \frac{1}{K}\)) gefüllt, d.h., die Tasse enthält nun ganz genau \(300 \, ml\) Kaffee. Tasse und Kaffee haben eine Temperatur von \(T_2 = 90^\circ C\). Aber Herr Müller hat Zeit und keine Antipathie gegen kalten Kaffee. So wartet er, bis Tasse und Kaffee auf Raumtemperatur (\(T_1 = 20^\circ C\)) abgekühlt sind. Jetzt kann er genau \(2,89 \,ml\) Milch hinzugeben. Berechne die Raumausdehnungszahl \(\gamma_T\) der Kaffeetasse.

Tipp: Hohlkörper dehnen sich so aus, als ob der Hohlraum aus dem gleichen Material wie die Hohlraumwände bestehen würde.

\(V \left( T + \Delta T\right) = V_0 \left( 1 + \gamma \Delta T \right)\)

\(V_K \left( T + \Delta T\right) = V_K \left( T_2 \right)\)

\(V_T \left( T + \Delta T\right) = V_T \left( T_2 \right)\)

\(V_K \left( T_2 \right) = V_T \left( T_2 \right)\)

\(V_T \left( T_1 \right) = V_K \left( T_1 \right) + V_M \left( T_1 \right)\)

\(V_K \left( T_2 \right) = V_K \left( T_1 \right) \left(1 + \gamma_K \Delta T \right) \Leftrightarrow V_K \left( T_1 \right) = \frac{V_K \left( T_2 \right)}{1 + \gamma_K \Delta T } = 296.26 \, ml\)

\(V_T \left( T_1 \right) = V_K \left( T_1 \right) + V_M \left( T_1 \right) = 296.26 \, ml + 3.54 \, ml = 299.8 \, ml\)

\(V_T \left( T_2 \right) = V_T \left( T_1 \right) \left(1 + \gamma_T \Delta T \right) \Leftrightarrow \gamma_T = \frac{1}{\Delta T} \left( \frac{V_T \left( T_2 \right)}{V_T \left( T_1 \right)} - 1 \right) = 0.0000095 \, \frac{1}{K} \approx 10^{-6} \frac{1}{K} \longrightarrow \text{Porzellan}\)