2.5. Schiefer Wurf

Eine besondere zweidimensionale Bewegung, welche oft betrachtet wird, ist der schiefe Wurf. Dieser beschreibt die zweidimensionale Bewegung eines Massenpunktes im (erdnahen) Gravitationsfeld. Dabei entspricht die Bewegung in der Richtung senkrecht zur Erdoberfläche dem freien Fall (mit beliebiger Anfangsgeschwindigkeit) und die Bewegung parallel zur Erdoberfläche entspricht einer Bewegung ohne Beschleunigung.

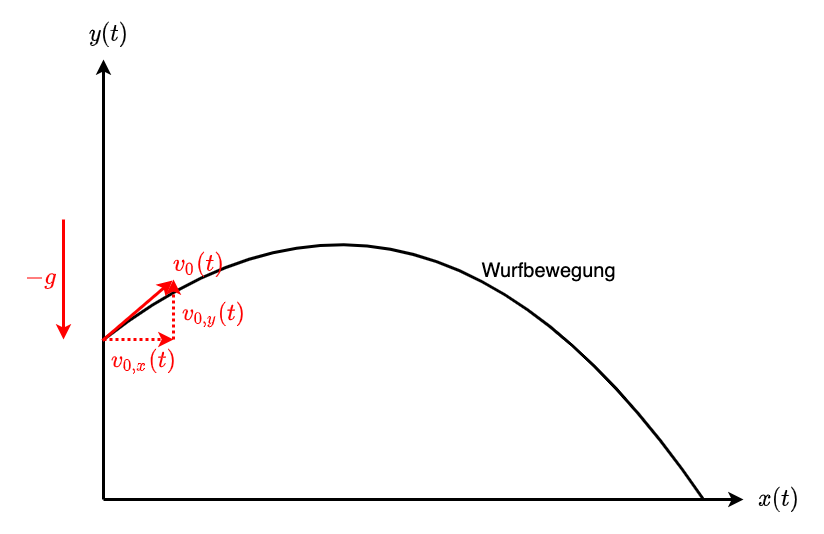
Fig. 2.13 Schiefer Wurf

Da es sich um eine freie Bewegung handelt, können x- und y-Richtung unabhängig voneinander betrachtet werden.

In x-Richtung gilt:

\(a_x = 0\)

\(v_x (t) = v_{0,x}\)

\(x(t) = v_{0,x} \cdot t + x_0\)

In y-Richtung gilt:

\(a_y = -g\)

\(v_y (t) = -g\cdot t + v_{0,y}\)

\(y(t) = - \frac{1}{2} \cdot g \cdot t^2 + v_{0,y} \cdot t + y_0\)

Die Größen \(v_{0,x}\), \(v_{0,y}\), \(x_0\) und \(y_0\) ergeben sich aus den Anfangsbedingungen.