4.3. Scheinkräfte im rotierenden Bezugssystem

Auch und insbesondere bei Drehbewegungen treten Scheinkräfte auf. Bei der Drehbewegung gibt es ein resultierendes Drehmoment und somit auch eine Kraft. Ein rotierendes Bezugssystem ist damit definitionsgemäß ein beschleunigtes Bezugssystem und somit kein Inertialsystem.

Scheinkräfte im rotierenden Bezugssystem sind besonders interessant, da wir uns auf der Erde in einem solchen Bezugssystem befinden.

4.3.1. Beispiel: rotierendes Bezugssystem

Ein weiteres, häufig in der Realität verwendetes, Bezugssystem, ist ein Bezugssystem, welches mit konstanter Geschwindigkeit rotiert. Dies wird im Folgenden betrachtet.

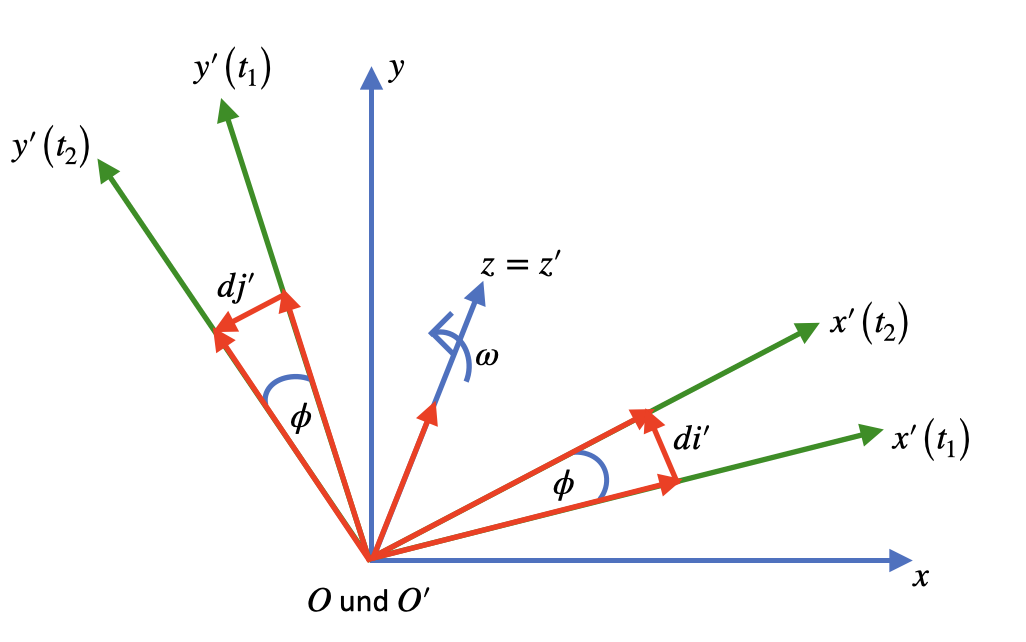
Fig. 4.8 Scheinkräfte in einem rotierenden Bezugssystem.

Durch ähnliche Betrachtungen wie in Scheinkräfte, ergibt sich im Bezugssystem \(O^\prime\):

\(m \ddot{\vec{r}}^\prime = m\vec{a}^\prime = -2m \left(\vec{\omega} \times \dot{\vec{r}}^\prime \right) - m \vec{\omega} \times \left(\vec{\omega} \times \vec{r}^\prime \right)\)

Dies bedeutet, dass es in diesem Fall zwei auftretende Scheinkräfte gibt. Die eine

\(\vec{F}_Z = - m \vec{\omega} \times \left(\vec{\omega} \times \vec{r}^\prime \right)\)

wird als Zentrifugalkraft bezeichnet, die andere als Corioliskraft.

\(\vec{F}_C = -2m \left(\vec{\omega} \times \dot{\vec{r}}^\prime \right) \)

Eine genaue Herleitung dieser Zusammenhänge ist beispielsweise in [Nol13] S. 184 zu finden. Diese überschreitet aber den Rahmen dieser Vorlesung und ist hier nur der Vollständigkeit halber abgegeben.