1.2. Polarkoordinaten

Ein weiteres häufig genutztes Koordinatensystem ist das der Polarkoordinaten. Dieses ist ein Koordinatensystem mit zwei Achsen. Diese sind jedoch im Gegensatz zum kartesischen Koordinatensystem nicht beide linear.

Bei den Polarkoordinaten werden die Achsen wie folgt gewählt (siehe Abbildung Abbildung 1.4): Die \(r\)-Achse gibt den Abstand zum Koordinatenursprung an. Die \(\phi\)-Achse gibt den Winkel zum Koordinatenursprung an.

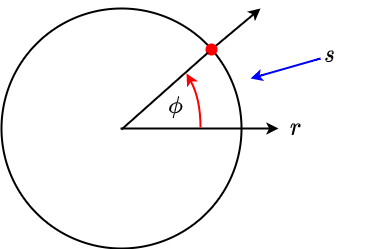
Fig. 1.4 Polarkoordinaten

Mit dem kartesichen zweidimensionalen Koordinatensystem ergibt sich folgender Zusammenhang

\( \vec{r} = \left(\begin{array}{c} x \\ y \end{array}\right) \longrightarrow \left(\begin{array}{c} r \cdot cos \left( \phi \right) \\ r \cdot sin \left( \phi \right) \end{array}\right) \)

Vorteil dieser Betrachtungsweise ist, dass beispielsweise bei Kreisbewegungen der Radius konstant ist und das zuvor zweidimensionale Problem auf ein eindimensionales Problem reduziert werden kann. Ist \(r\) eine Konstante, verbleibt nur noch der Winkel \(\phi\) als Variable.

Für die auf dem Kreisbogen zurückgelegte Strecke \(s\) (auch Bogenmaß genannt) gilt

\(s = r \cdot \phi\)