1. Flüssigkeiten#
Elemente können in drei verschiedenen Aggregatzuständen vorkommen, diese sind fest, flüssig und gasförmig.
In welcher Form das Element vorkommt, hängt von der Temperatur des Elementes ab. Die Temperatur ist definiert als ein Maß für die mittlere kinetische Energie aller Teilchen. Die kinetische Energie der Teilchen beschreibt die Bewegung der Teilchen, die Art der Bewegung ist in den drei Aggregatzuständen jedoch völlig unterschiedlich. Im Festkörper sind die Teilchen fest in einer Gitterstruktur gefunden und schwingen die Teilchen nur um ihre Ruhelage. In der Flüssigkeit ist diese Gitterstruktur aufgebrochen, die Teilchen sind aber noch eng zusammen. Bei Bewegung müssen sich die Teilchen durch Lücken zwischen ihren Nachbarn hindurch zwängen (Diffusion, Brownsche Molekularbewegung). Im Gas haben die Teilchen die höchste kinetische Energie. Hier bewegen sie sich mit großem Abstand zueinander und die Teilchen bewegen sich geradlinig wie Billardkugeln, bis sie mit einem anderen oder mit der Gefäßwand zusammen stoßen.
Flüssigkeiten können wir folgt beschrieben werden:
Die Moleküle bzw. Atome sind nicht wie beim Festkörper in eine Gitterstruktur eingebunden, sondern können sich gegenseitig verschieben. Bei Erhöhung der Temperatur werden die Teilchenbewegungen immer schneller. Die Abstände zwischen den Teilchen sind gering, die Teilchen wechselwirken weiter miteinander.
Auf einer makroskopischen Skala betrachtet sind Flüssigkeiten Stoffe, die einer Formänderung so gut wie keinen, einer Volumenänderung hingegen einen recht großen Widerstand entgegensetzt
\(\Rightarrow\) Flüssigkeiten passen sich der Form an, sind jedoch inkompressibel
1.1. Oberflächenspannung#
Die Oberflächenspannung ist ein Phänomen zwischen Flüssigkeiten und Gasen. Die Oberflächenspannung bewirkt, dass Gegenstände schwimmen, die aufgrund der größeren Dichte eigentlich untergehen müssten oder dass Farben auf manchen Oberflächen sehr gut benetzen während sie auf anderen einfach abperlen (Lotuseffekt)
In Flüssigkeiten befinden sich die einzelnen Moleküle im Gleichgewicht in einem festen Abstand voneinander, ohne jedoch eine Gitterstruktur wie bei Festkörpern aufzuweisen. Dieser Abstand ist gekennzeichnet durch ein Gleichgewicht abstoßender und anziehender Kräfte innerhalb der Wirkungssphäre des einzelnen Moleküls in der Flüssigkeit (elektrostatische Wechselwirkung) Im Gas Wechselwirkung nur durch Stoßprozesse
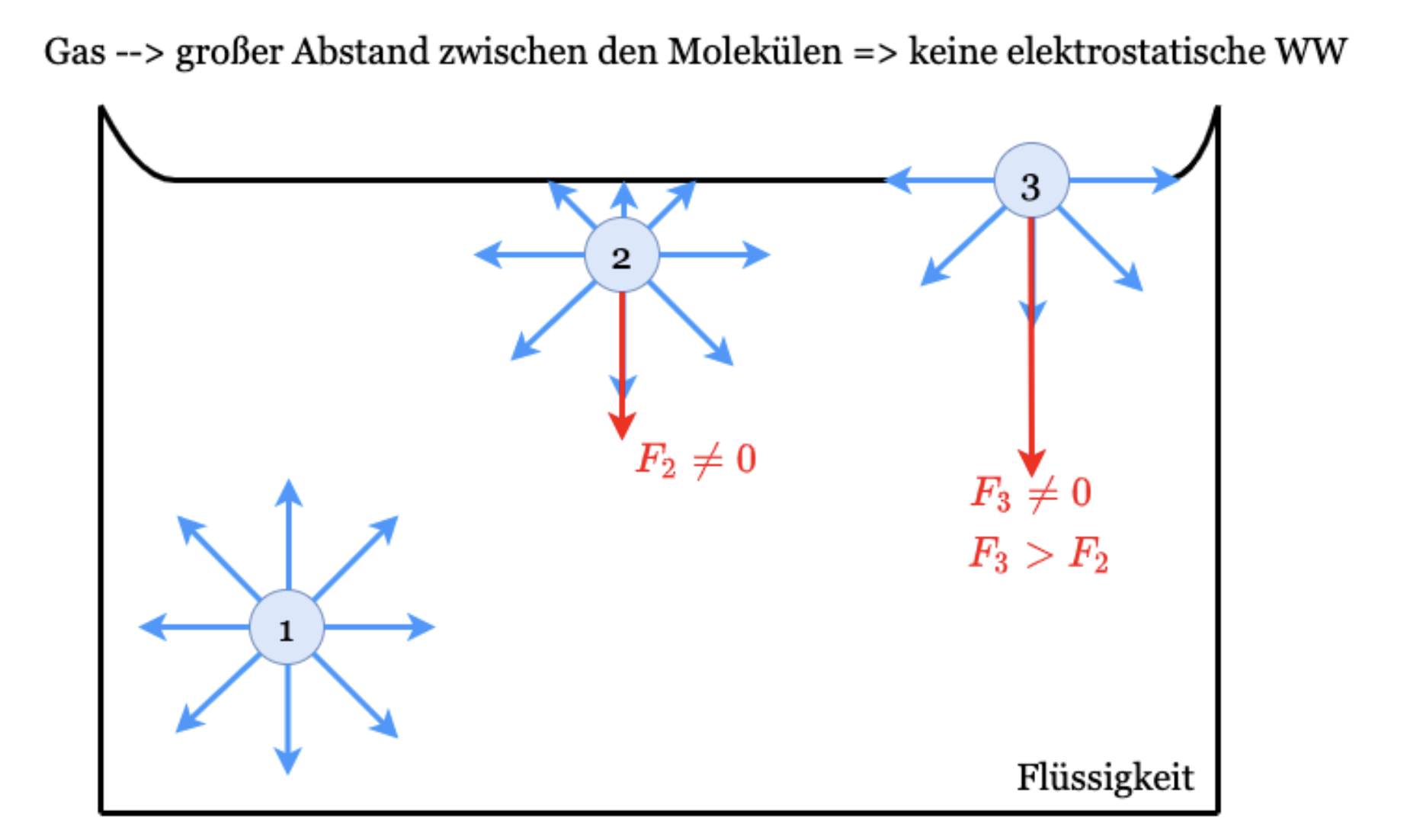
Fig. 1.11 Darstellung der Wechselwirkung an der Grenzfläche zwischen Flüssigkeiten und Gasen.#
Den maximalen Wert erreicht die nach innen gerichtete Kraft, wenn sich das Molekül direkt an der Grenzfläche zum Gas befindet, diese Grenzfläche wirkt dann wie eine dünne Membran. Zur Überwindung dieser nach innen gerichteten Kraft ist Arbeit notwendig (wenn man das Molekül aus der Flüssigkeit herauslösen will). Somit besitzen alle direkt an der Oberfläche liegenden Moleküle eine sogenannte potentielle Energie, welche als Oberflächenenergie bezeichnet wird.
Wird nun eine Oberfläche \(A\) um \(\Delta A\) vergrößert, erfordert dies den Transport von Molekülen in Richtung Oberfläche. Dies resultiert in einer zur Oberflächenänderung \(\Delta A\) proportionalen Arbeit \(\Delta W\).
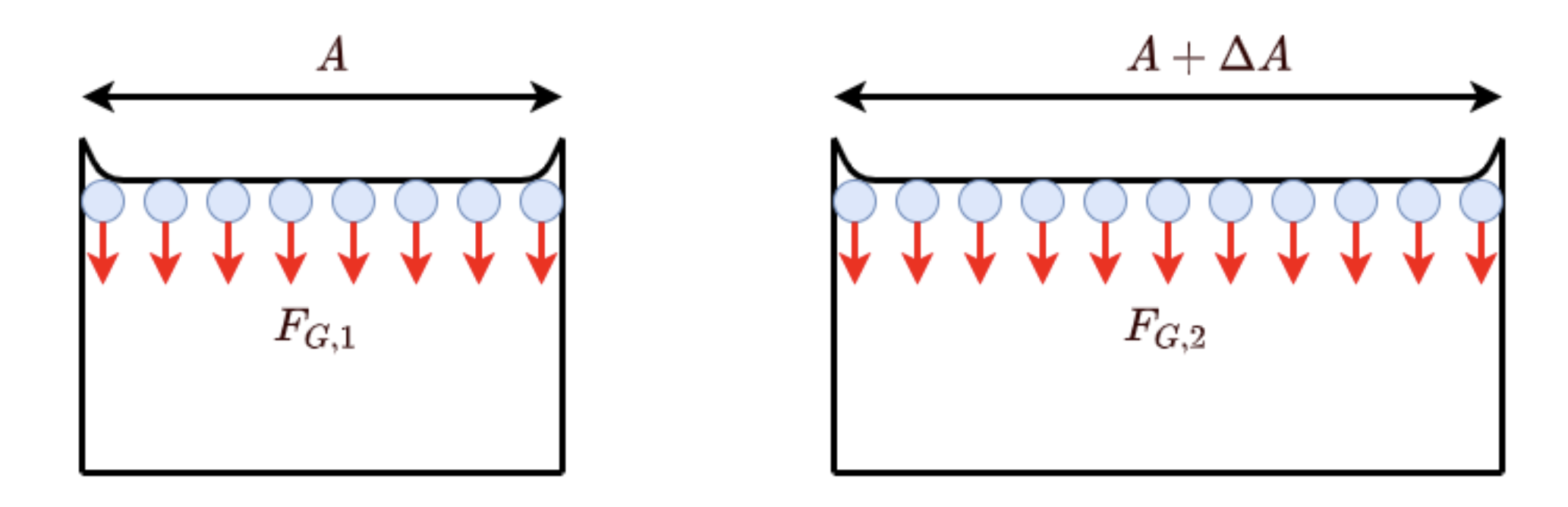
Fig. 1.12 Darstellung der Oberflächenspannung#
Die Oberflächenspannung ist definiert als der Proportionalitätsfaktor \(\sigma = \frac{\Delta W}{\Delta A}\) mit \(\Delta W = F \Delta s\).
1.1.1. Messung der Oberflächenspannung#
Fig. 1.13 Darstellung der Bügelmethode zur Messung der Oberflächenspannung.#
Bei der Bügelmethode (Abreißmethode) wird ein Bügel mit einem darin eingelöteten extrem dünnen Draht in die Flüssigkeit gehängt, sodass dieser gerade in die Flüssigkeit eintaucht und von dieser benetzt wird. Mit einer Präzisionsfederwaage wird dann die Zugkraft am Bügel nach und nach erhöht. Der Draht wird dann aus der Flüssigkeit gezogen und zieht einen Flüssigkeitsfilm mit. An einem bestimmten Punkt reißt dieser Film ab.
\(\longrightarrow\) sehr präzise Waagen notwendig (im \(mg\) Bereich).
Die Oberflächenspannung ist dann gegeben durch
\(\sigma = \frac{\Delta W}{\Delta A} = \frac{F \cdot \Delta x}{2 \cdot \Delta x \cdot l} = \frac{F}{2 \cdot l}\)
Anmerkung: Faktor 2 bei der Fläche wegen Vorder- und Rückseite des Films.
Die Oberflächenspannung von Wasser kann durch Zugaben von beispielsweise Spülmittel stark reduziert werden, so dass die Wasserhaut dann an der Zugabestelle auseinanderreisst.
Fig. 1.14 Reduktion der Oberflächenspannung durch Spülmittel#
1.2. Kohäsion und Adhäsion#
Nicht nur zwischen Flüssigkeiten und Gasen finden eine Wechsenwirkung statt, sondern auch die Wechselwirkung zwischen Feststoffen und Flüssigkeiten und führt zu Bindungskräften. Die Theorie zur Berechnung der Kräfte ist sehr komplex, man kann jedoch qualitativ zwischen zwei verschiedene Effekten unterscheiden.
Kohäsion Beschreibt die Tendenz von Molekülen gleichen Typs innerhalb eines Stoffes zusammenzuhalten
Adhäsion Beschreibt die Tendenz von Molekülen unterschiedlichen Typs aneinander zu haften
1.2.1. Kapillareffekt#
Ein Effekt, der durch die Wechselwirkung zwischen Kohäsion und Adhäsion hervorgerufen wird, ist der Kapillareffekt. Hier ist die Kohäsion kleiner als die Adhäsion. Der Kapillareffekt ist das Verhalten von Flüssigkeiten bei Kontakt mit Kapillaren, also genügend engen Röhren, Spalten oder Hohlräumen in Feststoffen. Ist die Adhäsion größer als die Kohäsion, ist die Wechselwirkung zwischen Wand und Flüssigkeit größer, als die Wechselwirkung der Wassermoleküle untereinander, das Wasser wird daher an den Wänden hochgezogen (siehe Abbildung 1.15). In dünnen Röhren ist das Gewicht der Flüssigkeit gering, der Kapillareffekt ist daher stärker als die Schwerkraft. Der Kapillareffekt sorgt dafür, dass Wasser aus den Wurzeln von Bäumen bis in die Blätter aufsteigt und das Wasser in engen Felsspalten nach oben befördert wird.
Fig. 1.15 Kohäsion < Adhäsion#
Die kapillare Steighöhe kann berechnet werden durch
\(h = \frac{2 \cdot \sigma \cdot cos \left( \alpha \right)}{\rho \cdot g \cdot r}\)
mit \(\sigma = \) Oberflächenspannung
\(\rho = \) Dichte der Flüssigkeit
\(\alpha = \) Winkel der Adhäsion
\(g = \) Erbeschleunigung
\(r = \) Radius der Kapillarröhre
Beim Kapillareffekt ist \(\alpha < 90^\circ\)
Für Wasser gilt \(\alpha = 20 ^\circ \Rightarrow cos \left( \alpha \right) = 0.939... \approx 1\)
\(\Rightarrow h = \frac{2 \cdot \sigma}{\rho \cdot g \cdot r}\)
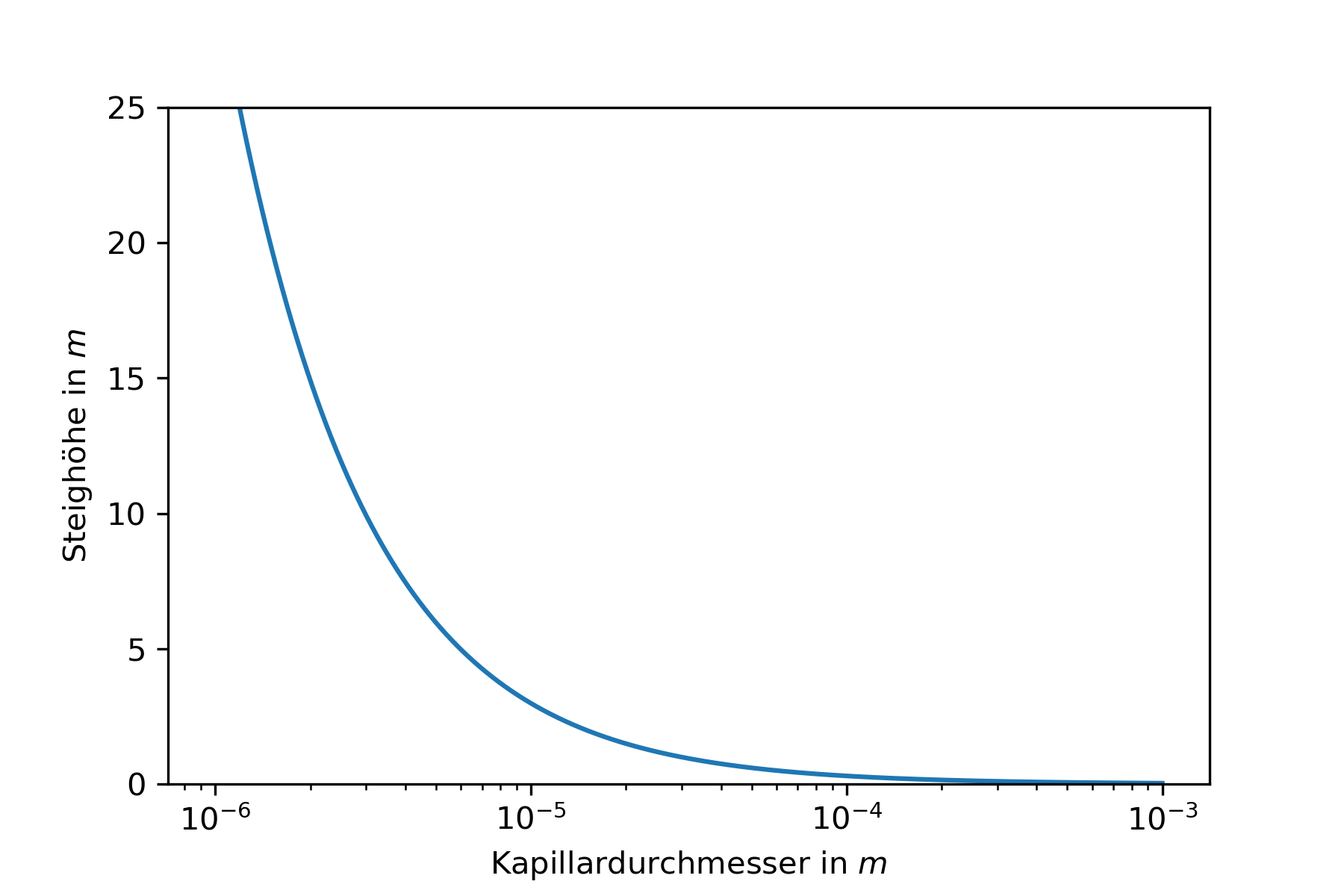
Fig. 1.16 Kapillare Steighöhe von Wasser#
Fig. 1.17 Unterschiedliche Steighöhen in verschieden dicken Kapillaren.#
Auch beim Löten hat der Kapillareffekt eine große Bedeutung. Das flüssige Lot fließt beim Löten durch die Kapillarwirkung zwischen den Draht und die Platinenbohrung. Das Lot bleibt in dem Zwischenraum und fließt nicht nach unten durch. Daher kann das Lot allein durch Hitze nicht entfernt werden, zum Entlöten werden Hilfsmittel (Entlötpumpe oder -Litze) benötigt.
Fig. 1.18 Kapillareffekt beim Löten#
1.2.2. Kohäsion > Adhäsion#
Ist die Kohäsion größer als die Adhäsion, tritt ein umgekehtrer Effekt auf und \(\alpha > 90^\circ\)
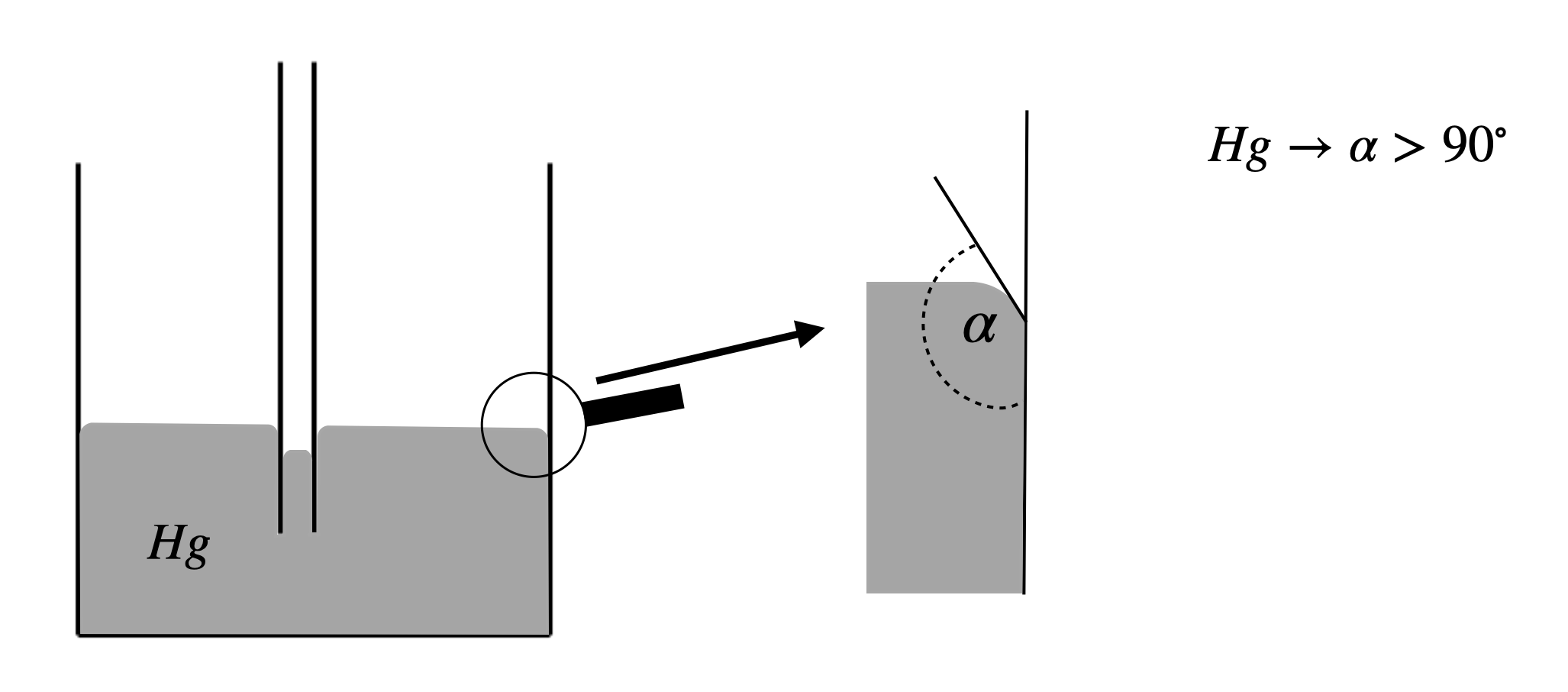
Fig. 1.19 Kohäsion > Adhäsion#
