3.8. Scheinkräfte#
Scheinkräfte sind Kräfte die vom Bezugssystem, in dem ein physikalischer Vorgang betrachtet wird, abhängen. Scheinkräfte gibt es daher nicht in Inertialsystemen, sondern nur in beschleunigten Bezugssystemen. Scheinkräfte werden auch als Trägheitskräfte bezeichnet, Beispiele sind:
Kräfte beim Anfahren und Abbremsen
Kräfte in rotierenden Bezugssystemen
Scheinkräfte genügen nicht dem Prinzip von Actio und Reactio, denn es gibt keinen zweiten Körper, von dem sie ausgehen.
3.8.1. Beispiel: negativ beschleunigtes Bezugssystem#
Um das Prinzip von Scheinkräften näher zu erläutern, wird nun folgendes Beispiel betrachtet.
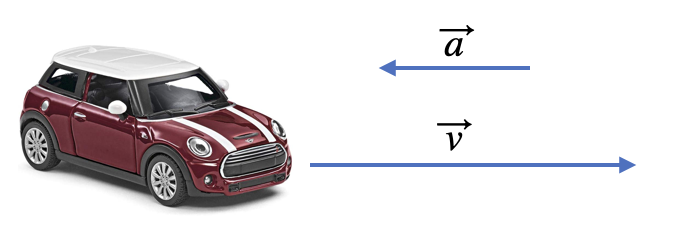
Fig. 3.14 Scheinkraft in einem negativ beschleunigten Bezugssystem.#
Ein Auto bewegt sich mit \(v= 100 \frac{km}{h}\) und bremst mit \(a = - 5 \frac{m}{s^2}\). Im Auto befindet sich auf dem Beifahrersitz eine Flasche Wasser (Inhalt \(0.7 \, l\)). Welche Beschleunigung erfährt die Flasche beim Bremsvorgang gesehen vom Auto aus?
Hierzu wird die Galilei-Transformation verwendet, um vom Bezugsystem \(O\) (das Bezugssystem Strasse, in dem das Auto von aussen betrachtet wird) zum Bezugssystem \(O^\prime\) (das Bezugssystem, welches sich mit dem Auto mitbewegt, also mit \(a\) beschleunigt wird) überzugehen.
mit
\(\vec{a}_{O \rightarrow O^\prime} = -5 \frac{m}{s^2}\) und \(\vec{v}_{0, O \rightarrow O^\prime} = 100 \frac{km}{h}\)
gilt daher
\(O^\prime \rightarrow O\) |
\(O \rightarrow O^\prime\) |
|---|---|
\( \vec{r} = \vec{r}^\prime + \frac{1}{2} \vec{a}_{O \rightarrow O^\prime} t^2 + \vec{v}_{0, O \rightarrow O^\prime}t\) |
\( \vec{r}^\prime = \vec{r} - \frac{1}{2} \vec{a}_{O \rightarrow O^\prime} t^2 - \vec{v}_{0, O \rightarrow O^\prime}t\) |
\( \vec{v} = \vec{v}^\prime + \vec{a}_{O \rightarrow O^\prime}t + \vec{v}_{0, O \rightarrow O^\prime}\) |
\( \vec{v}^\prime = \vec{v} - \vec{a}_{O \rightarrow O^\prime} t - \vec{v}_{0, O \rightarrow O^\prime}\) |
\( \vec{a} = \vec{v}^\prime + \vec{a}_{O \rightarrow O^\prime}\) |
\( \vec{a}^\prime = \vec{a} - \vec{a}_{O \rightarrow O^\prime}\) |
Im beschleunigten Bezugssystem \(O^\prime\) gilt daher \(\vec{a}^\prime = \vec{a} - \vec{a}_{O \rightarrow O^\prime}\). Damit wirken hier folgende Kräfte
\(\Rightarrow F_{O^\prime} = m \cdot \vec{a}^\prime = m\cdot \vec{a} - m \cdot \vec{a}_{O \rightarrow O^\prime} = - m \cdot \left(- 5 \frac{m}{s^2} \right)= m \cdot 5 \frac{m}{s^2}\)
Die Kraft \(- m \cdot \vec{a}_{O \rightarrow O^\prime}\) ist die Scheinkraft, die durch die Beschleunigung des Bezugssystems bewirkt wird. Anschaulich gesprochen wird das Bezugssystem (das Auto) gebremst, dadurch scheint es so, als ob die Flasche beschleunigt wird. Ein von aussen zuschauender Beobachter würde dagegen eine Flasche sehen, die sich mit konstanter Geschwindigkeit weiterbewegt, während das Auto gebremst wird.
