3.3. Integralrechnung#
Das Gegenstück zur Differentialrechnung ist die Integralrechnung. Das Integral wird mit einem \(\int f(x) \, dx\) gekennzeichnet. Das Integral oder auch die Stammfunktion einer Funktion ist diejenige Funktion, deren Ableitung wieder die Funktion ergibt. Da die Ableitung einer Konstanten immer Null ergibt, kann zu jeder Stammfunktion eine beliebige Konstante dazuaddiert werden. Die Stammfunktion wird oft mit einem \(F(x) = \int f(x) \, dx\) bezeichnet.
Beispiel:
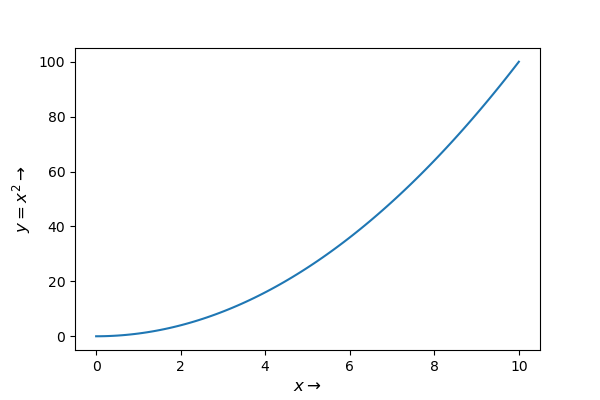
\(f(x) = x^2\)
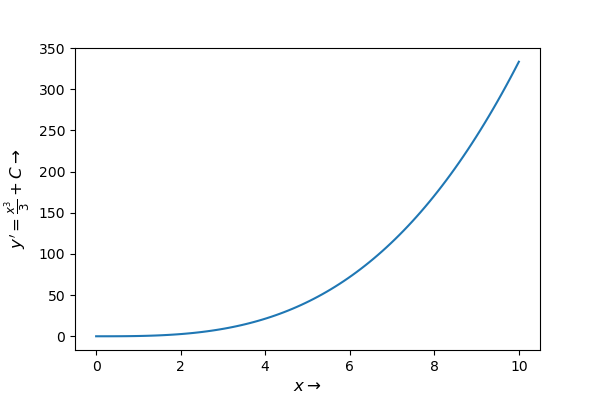
\(F(x) = \int x^2 \, dx = \frac{1}{3} x^3 + C\)
Beispiel einer Funktion |
Integral dieser Funktion |
|---|---|
|
|
Das finden von Stammfunktionen ist schwieriger als das Bilden von Ableitungen, da hier nicht für alle Fälle Rechenregeln zur Verfügung stehen. Es gibt jedoch einige Ansätze, die beim Finden der Stammfunktion helfen können.
Die wichtigsten sind hier zusammengefasst.
Ein bekanntes Nachschlagewerk ist der Bronstein.
Eine besondere Bedeutung hat das bestimmte Integral \(\int_a^b f(x) \, dx\). Für dieses gilt
\(\int_a^b f(x) \, dx = F(b) - F(a)\).
Es beschreibt die Fläche S, die von der Funktion f(x) eingeschlossen wird.