4. Vektorrechnung

Definitionen

Skalare sind Größen, die einen Zahlenwert, aber keine Richtung haben. Beispiele: Anzahl, Länge, Dichte, Temperatur von Objekten.

Vektoren sind Größen, die einen Zahlenwert und eine Richtung haben. Beispiele: Geschwindigkeit, Erdanziehung, Magnetfeld

Beispiel

Ein Auto fährt mit der Geschwindigkeit von \(v = 100 \frac{km}{h}\). (d.h. der Zahlenwert der Geschwindigkeit ist gegeben). Das ist nicht die ganze Information über die Geschwindigkeit: es ist nicht gesagt wohin und in welcher Richtung das Auto fährt. Die vektorielle Grösse \(\vec{v}\) enthält den Betrag und die Richtung.

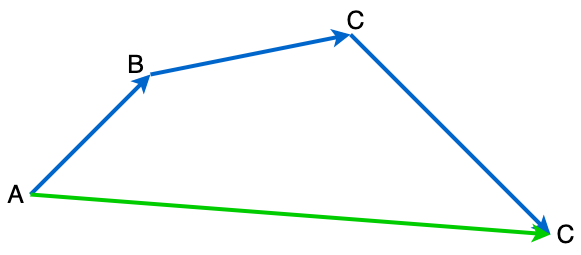
Fig. 4.1 Darstellung einer Vektoraddition.

Der Vektor \(\vec{AD}\) gibt die Verschiebung und die Richtung an. Die Länge des Vektors \(\left| \vec{AD} \right|\) entspricht dem Betrag (skalarem Zahlenwert) des Vektors. Das entspricht der Vektoraddition

\(\vec{AD} = \vec{AB} + \vec{BC} + \vec{CD}\).

Dies kann auch in der Koordinatenschreibweise dargestellt werden.

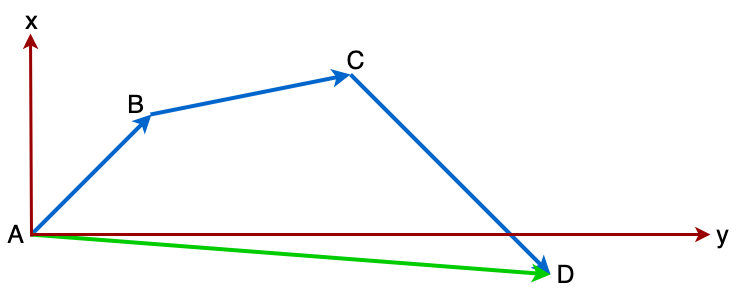
Fig. 4.2 Darstellung einer Vektoraddition in Koordinatenschreibweise.

Dies entspricht dann

\(\vec{AD} = \left(\begin{array}{c} x_{AD} \\ y_{AD} \\ z_{AD} \end{array}\right) = \left(\begin{array}{c} x_{AB} + x_{BC} + x_{CD} \\ y_{AB} + y_{BC} + y_{CD} \\ z_{AB} + z_{BC} + z_{CD} \end{array}\right)\)