Beispielaufgaben zum Schiefen Wurf

2.6. Beispielaufgaben zum Schiefen Wurf#

2.6.1. Vergessene Autoschlüssel#

Ein Segler fährt mit seinem Boot eine Runde über den Kemnader See. Zwischendurch fällt ihm ein, dass er seinen Autoschlüssel noch in der Tasche hat. Sein an Land gebliebener Kumpel braucht den Autoschlüssel allerdings. Da der Segler keine Lust hat mit dem Boot anzulegen, will er seinem am Ufer stehenden Kumpel den Schlüssel zuwerfen. Nehmen Sie an, dass das Boot eine Entfernung von \(10 m\) vom Ufer hat.

  1. Fertigen Sie zunächst eine Skizze an und zeichnen Sie ein Koordinatensystem, bei dem die \(x\)-Richtung horizontal vom Boot zum Ufer verläuft und die \(y\)-Koordinaten senkrecht dazu nach oben. Reibungseffekte können vernachlässigt werden.

  2. In welchem Winkel wird der Schlüssel geworfen, wenn zu Beginn des Wurfes die Geschwindigkeit in \(x\)- und \(y\)-Richtung gleich ist.

  3. Berechnen Sie den Betrag der Anfangsgeschwindigkeit?

Lösung

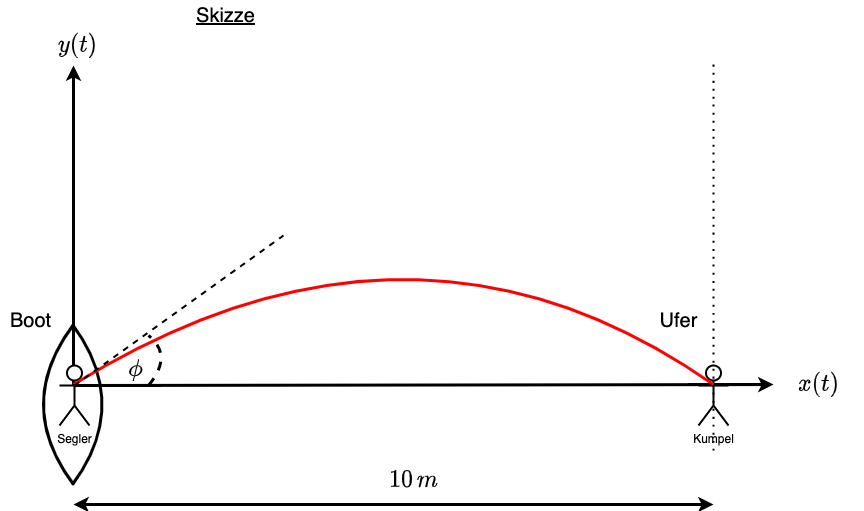
../../../_images/SchieferWurf-out.png

Fig. 2.14 Skizze und Koordinatensystem#

in \(x\)-Richtung gilt:

  • keine Beschleunigung

  • \(v_{x0} = \text{konst.}\)

  • Bewegungsgleichung in \(x\)-Richtung: \(v_{x0} = \text{konst.}\) \(x(t) = v_{x0}\cdot t + x_0\)

  • Wurf beginnt bei \(x_0 = 0\) und damit ist \(x(t) = v_{x0}\cdot t\)

in \(y\)-Richtung gilt:

  • Beschleunigung \(a = -g\)

  • Wurf beginnt bei \(y_0 = 0\)

  • Bewegungsgleichungen in \(y\)-Richtung: \(a = \text{konst.} = -g\) \(v_y(t) = -gt+v{y0}\) \(y(t) = -\frac{1}{2}g t^2 + v_{y0}\cdot t\)

  • Wurf beginnt bei \(x_0 = 0\) und damit ist \(x(t) = v_{x0}\cdot t\)

Bekannt ist:

  • Wurfweite \(l = x\left( t_e\right)\)

  • Gleiche Startgeschwindigkeit in \(x\)- und \(y\)-Richtung \(\Rightarrow v_{x0}\ = v_{y0}\)

Damit gilt:

\(x(t_e) = l = v_{x0} t_e \Leftrightarrow t_e = \frac{l}{v_{x0}}\)

Zum Zeitpunkt \(t_e\) hat der Schlüssel wieder die Höhe \(y \left( t_e \right) = 0\)

\(y(t_e) = 0 = - \frac{1}{2} g t_e^2 + v_{y0} t_e \Leftrightarrow t_e = \frac{l}{v_{x0}}\)

Daraus ergibt sich:

\(\left. \Rightarrow 0 = - \frac{1}{2} g \left(\frac{l}{v_{x0}}\right)^2 + v_{y0} \frac{l}{v_{x0}} \right| \cdot v_{x0}^2\) \(\left. \Leftrightarrow - \frac{1}{2} g l^2 + v_{x0} v_{y0}l\right| :l\) \(\left. \Leftrightarrow v_{x0} v_{y0} = \frac{1}{2} g l \right| v_{x0}\ = v_{y0} \) \(\Rightarrow v_{x0}^2 = \frac{1}{2} g l\) \(\Rightarrow v_{x0} = v_{y0} = \sqrt{ \frac{1}{2} g l } = \sqrt{ \frac{1}{2} g 10 m }\)

und

\(v_0 = \sqrt{v_{0x}^2 +v_{0y}^2} = \sqrt{\frac{1}{2} g 10 m +\frac{1}{2} g 10 m } = \sqrt{g 10 m } = 9.9 \, \frac{m}{s}\)

Für den Abwurfwinkel gilt:

\(tan \left( \phi \right) = \left( \frac{v_{y0}}{v_{x0}} \right) = 1 \Rightarrow \phi = arctan \left( 1 \right) = 45^\circ\)

2.6.2. Schraubendreher#

Herr Müller möchte am Balkon einen Blumenkasten anschrauben. Leider fällt ihm dabei aus Versehen der Schraubendreher vom Boden des Balkons aus dem zweiten Stock (Höhe h = 5 m). Zum Glück wird niemand getroffen. Eine vorbeilaufende Spaziergängerin sieht das ganze und fragt, ob sie den Schraubendreher wieder nach oben werden soll. Die Spaziergängerin steht 2 m weiter vom Haus weg, als der Balkon hervorsteht.

  1. Unter welchem Winkel und mit welcher Anfangsgeschwindigkeit muss der Schraubendreher geworfen werden bei einer Abwurfhöhe von 2m, damit Herr Müller dem Schraubendreher in einem Meter Höhe am Balkonrand fangen kann?

  2. Zeichnen Sie zuerst eine Skizze der Situation.

Lösung

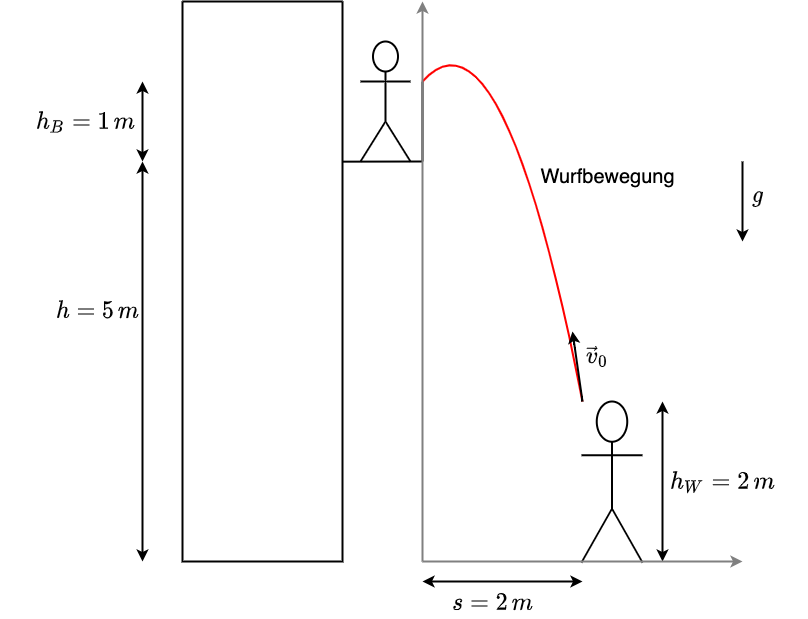
../../../_images/Balkon_Schraubendreher.png

Fig. 2.15 Skizze und Koordinatensystem#

Contents