2. Trägheitsmoment

Um die Drehbewegung eines starren Körpers zu beschreiben, werden Trägheitsmomente verwendet. Um den Begriff des Trägheitsmomentes zu verstehen, bietet sich der Vergleich mit der Kreisbewegung eines Massenpunktes an.

Fig. 2.16 Kreisbewegung einer Punktmasse.

Der Drehimpuls ist dabei:

\(\vec{L} = m \cdot \left( \vec{v} \times \vec{r} \right)\)

Da bei der Kreisbewegung \(\vec{v} \perp \vec{r}\) ist, gilt:

\(\Rightarrow \left| \vec{L} \right| = m \cdot v \cdot r = m \cdot \omega r \cdot r = m r^2 \omega\)

Analog zum Impuls \( \vec{p} = m \cdot \vec{v}\) definiert man dann das Trägheitsmoment \(\Theta\)

\(\vec{L} = \Theta \vec{\omega}\)

Für eine Punktmasse auf einer Kreisbahn ist demnach \( \Theta =: mr^2\)

Für Drehimpuls und Drehmoment gilt dann analog zu Impuls und Kraft der Zusammenhang

\(\vec{M} = \frac{d \vec{L}}{dt} = \Theta \frac{d \vec{\omega}}{dt} = \Theta \vec{\alpha}\)

wobei \(\vec{\alpha}\) die Winkelbeschleunigung ist.

Translation		Rotation
Kraft	\(\vec{F} = \frac{d \vec{p}}{dt}\)	Drehmoment	\(\vec{M} = \frac{d \vec{L}}{dt}\)
	\(\vec{F} = m \cdot \vec{a}\)		\(\vec{M} = \Theta \cdot \vec{\alpha}\)
Impuls	\(\vec{p}\)	Drehimpuls	\(\vec{L} = \vec{r} \times \vec{p}\)
	\(\vec{p} = m \cdot \vec{v}\)		\(\vec{L} =\Theta \cdot \vec{\omega}\)

Wie der Impuls bei der Translationsbewegung, ist der Drehimpuls bei der Drehbewegung eine Erhaltungsgröße, wenn kein äußeres Drehmoment anliegt.

2.1. Drehimpulserhaltung bei mehreren Massen

Im Folgenden wird nun ein einfacher starrer Körper, der aus drei fest miteinander verbundenen Massenpunkten besteht.

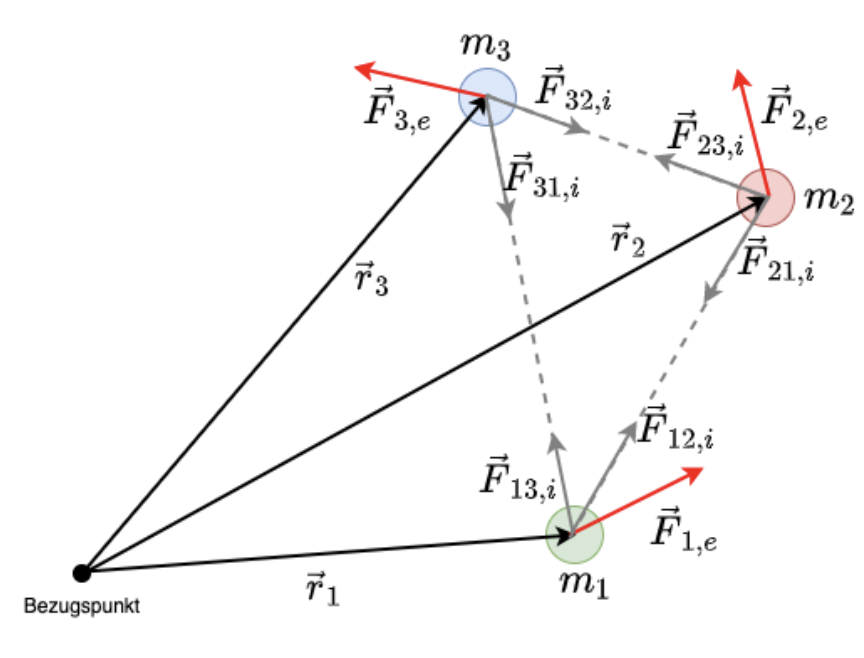
Fig. 2.17 Drehbewegung eines starren Körpers aus mehreren diskreten Massenpunkten.

Für \(m_1\) gilt:

\(\vec{M}_{1} = \vec{r}_{1} \times \left( \vec{F}_{1,e} + \vec{F}_{12,i} + \vec{F}_{12,i} \right)\)

Und äquivalent gilt nach Newton für \(\vec{M}_2\) und \(\vec{M}_3\)

\(\vec{F}_{kj,i} = - \vec{F}_{jk,i} \)

Zum Beispiel gilt:

\(\vec{r}_1 \times \vec{F}_{12,i} + \vec{r}_2 \times \vec{F}_{21,i} = \left( \vec{r}_1 -\vec{r}_2 \right) \times \vec{F}_{12,i} = 0\)

da \(\left( \vec{r}_1 - \vec{r}_2 \right) \parallel \vec{F}_{12,i}\)

Damit gilt \(\vec{M} = \sum_k \vec{M}_k = \sum_k \vec{M}_{k,e} \)

mit \(\vec{M}_k = \frac{d \vec{L}_k}{dt} = \vec{r}_k \times \left( \vec{F}_{k,e} + \sum_{k \not= j} \vec{F}_{kj,i} \right)\)

da die inneren Kräfte sich aufheben. Es gilt:

\(\frac{d \vec{L}}{dt} = \frac{d}{dt} \sum_k \vec{L}_k = \vec{M}\)

Greift kein äußeres Drehmoment an, ist der Gesamtdrehimpuls erhalten:

\(\vec{M} = 0 \Rightarrow \vec{L} = \sum_k \vec{L}_k = \text{konstant}\)

Für die Drehimpulse gilt \(\vec{L}_k = \Theta_k \vec{\omega}_k\)

Und damit \(\vec{L} = \Theta_1 \vec{\omega}_1 + \Theta_2 \vec{\omega}_2 + \Theta_3 \vec{\omega}_3\)

Da die Massen einen festen Abstand zueinander haben, gilt \(\vec{\omega}_1 = \vec{\omega}_2 = \vec{\omega}_3 =:\vec{\omega}\) und somit \(\vec{L} = \left(\Theta_1 + \Theta_2 + \Theta_3 \right)\vec{\omega}\)

Das gesamte Trägheitsmoment \(\Theta = \left(\Theta_1 + \Theta_2 + \Theta_3 \right)\) ist also die Summe der Trägheitsmomente der Massenpunkte.

2.2. Trägheitsmoment von starren Körpern

Wie in trägheitsmoment dargestell, ist das Trägheitsmoment einer Punktmasse mit Abstand \(r\) zur Drehachse und Masse \(m\)

\(\Theta = m \cdot r^2\)

Fig. 2.18 Übergang zur kontinuierlichen Massenverteilung

Trägheitsmoment eines infinitesimalen Masse-Elements mit Abstand \(r\) zur Drehachse und Masse \(dm\) ist somit

\(d\Theta = dm \cdot r^2\)

Für das Massenelement \(dm\) gilt mit \(\rho = \frac{m}{V}\) \(\Rightarrow dm = \rho dV\) Damit ist dann das Trägheitsmoment

\(\Theta = \int_V \, r^2 \rho \, dV\)

2.3. Beispiel: Trägheitsmoment eines dünnen Stabs

Fig. 2.19 Modell eines dünnen Stabes

Das Trägheitsmoment eines dünnen Stabes soll berechnen werden.

Allgemein gilt \(\Theta = \int_V \, r^2 \rho \, dV\)

Da da radiale Ausdehnung des Stabs vernachlässigbar ist \(\left( l \gg d \right)\) Daher wird das Volumenintegtal zum Längenintegral und die Dichte ist \(\rho = \frac{l}{m}\).

\(\Rightarrow \Theta = \int_l \, r^2 \rho \, dl\)

Dabei ist der Abstand \(r\) zur Drehachse (\(y\)-Achse) \(r = r_\perp \rightarrow x = \left[ -\frac{l}{2} .. \frac{l}{2} \right]\)

Und somit \(\Theta = \int_V r_\perp^2 \rho dV = \int_{-\frac{l}{2}}^{\frac{l}{2}} x^2 \frac{m}{l} \, dx = \left| \frac{1}{3} x^3 \frac{m}{l} \right|_{-\frac{l}{2}}^{\frac{l}{2}} = \frac{m}{3l} \left( \left( \frac{l}{2} \right)^3 - \left(- \frac{l}{2} \right)^3\right) = \frac{m}{3l} 2 \frac{l^3}{8} = \frac{m}{12} l^2\)

2.4. Beispiel: Trägheitsmoment einer Kugel

Fig. 2.20 Modell eines=r homogenen Kugel

Dichte einer homogenen Kugel: \(\rho = \frac{m}{V} = \frac{m}{\frac{4}{3}\pi R^3}\)

Abstand zur Rotationsachse (z.B. \(z\)-Achse) \(r_\perp^2 = x^2+y^2 = r^2 \, sin^2(\theta)\)

Integration in Kugelkoordinaten: \(dxdydz=r^2sin(\theta)d\theta d \phi\)

\(x = r \, sin(\theta) \, cos (\phi)\) \(y = r \, sin(\theta) \, sin(\phi)\) \(z = r \, cos (\theta)\)

\(\Theta = \int dV \rho r_\perp^2 = \frac{3 \,m}{4\pi R^3} \int_0^R \int_0^\pi \int_0^{2\pi} r^2 sin(\theta) r^2 sin^2(\theta) dr\, d\theta \, d\phi = \frac{3 \,m}{4\pi R^3} 2\pi \int_0^Rdr \, r^4 \int_0^\pi sin^3(\theta)\, d\theta = \frac{2}{3}m R^2\)

2.5. Übersicht Trägheitsmomente

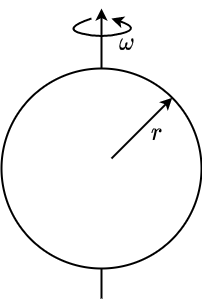
Fig. 2.21 \(\Theta = \frac{2}{5}mr^2\)

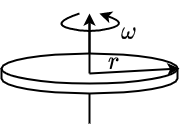
Fig. 2.22 \(\Theta = \frac{1}{2}mr^2\)

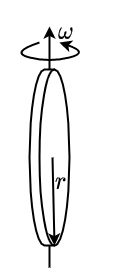
Fig. 2.23 \(\Theta = \frac{1}{4}mr^2\)

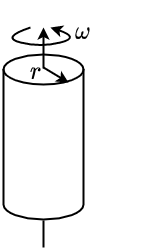
Fig. 2.24 \(\Theta = \frac{1}{2}mr^2\)

Fig. 2.25 \(\Theta = \frac{1}{6}ma^2\)

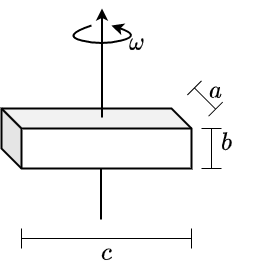
Fig. 2.26 \(\Theta = \frac{1}{12}m \left(b^2 + c^2\right)\)

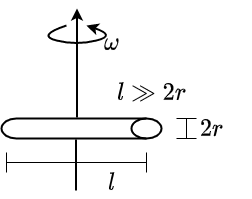
Fig. 2.27 \(\Theta = \frac{1}{12}ml^2\)

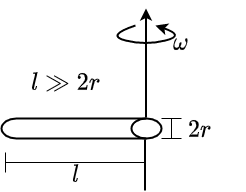
Fig. 2.28 \(\Theta = \frac{1}{3}ml^2\)

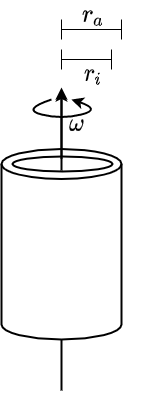
Fig. 2.29 \(\Theta = \frac{1}{2}m \left(r_a^2 +r_i^2\right)\)}

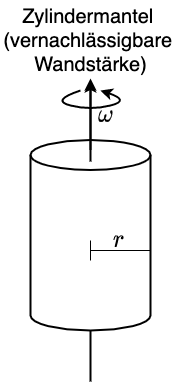
Fig. 2.30 \(\Theta \approx m r^2\)

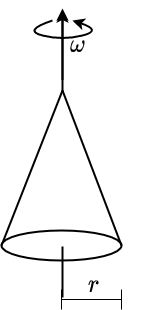
Fig. 2.31 \(\Theta = \frac{3}{10}m\,r^2\)

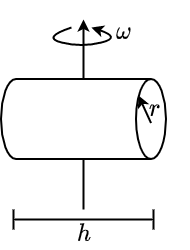
Fig. 2.32 \(\Theta = \frac{1}{4}m\,r^2 + \frac{1}{12}m\,l^2\)