2.1. Kinematik eines Massenpunktes

Der einfachste Fall ist die Bewegung eines Massenpunktes. Hier wird die komplette Masse des sich bewegenden Körpers in einem Punkt zusammengefasst, dieser besitzt dann keine räumliche Ausdehnung. In diesem Fall dient die funktionale Beschreibung dieses Massenpunktes dazu, die Bewegung des kompletten Körpers zu beschreiben.

Die Funktion \(\vec{r} = \vec{r}(t)\) beschreibt dann die Bewegung eines Massenpunktes. Die Zeit \(t\) ist hierbei das Element der Definitionsmenge. Der Ort \(\vec{x}\) ist die Position der Masse, also ein Element der Zielmenge. Damit ist \(\vec{r}\) eine Funktion von \(t\) oder auch \(\vec{r} = \vec{r}(t)\).

Im normalen Raum gibt es drei Dimensionen. Diese können beispielsweise durch drei Koordinaten

\( \vec{r} = \left(\begin{array}{c} x \\ y \\ z \end{array}\right)\)

beschrieben werden. Dies bedeutet, dass auch drei Gleichungen benötigt werden, um die Bewegung zu beschreiben.

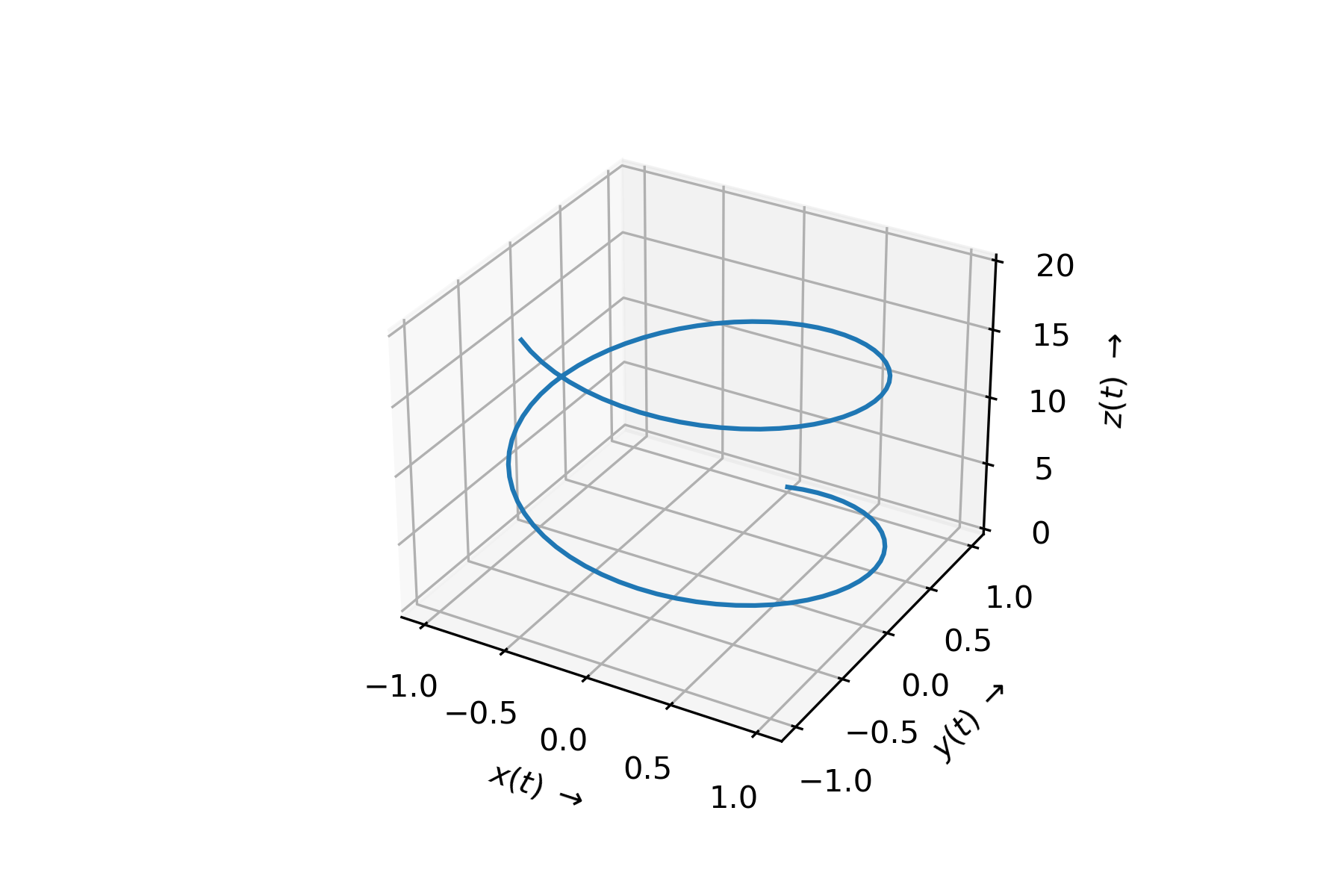
Fig. 2.1 Darstellung einer Bewegung in 3 Dimensionen.

Findet die Bewegung in weniger Dimensionen statt, werden auch entsprechenend weniger Gleichungen zur Beschreibung der Bewegung benötigt. So benötigt man zur beispielsweise zur Beschreibung der Bewegung in der Ebene 2 Gleichungen.

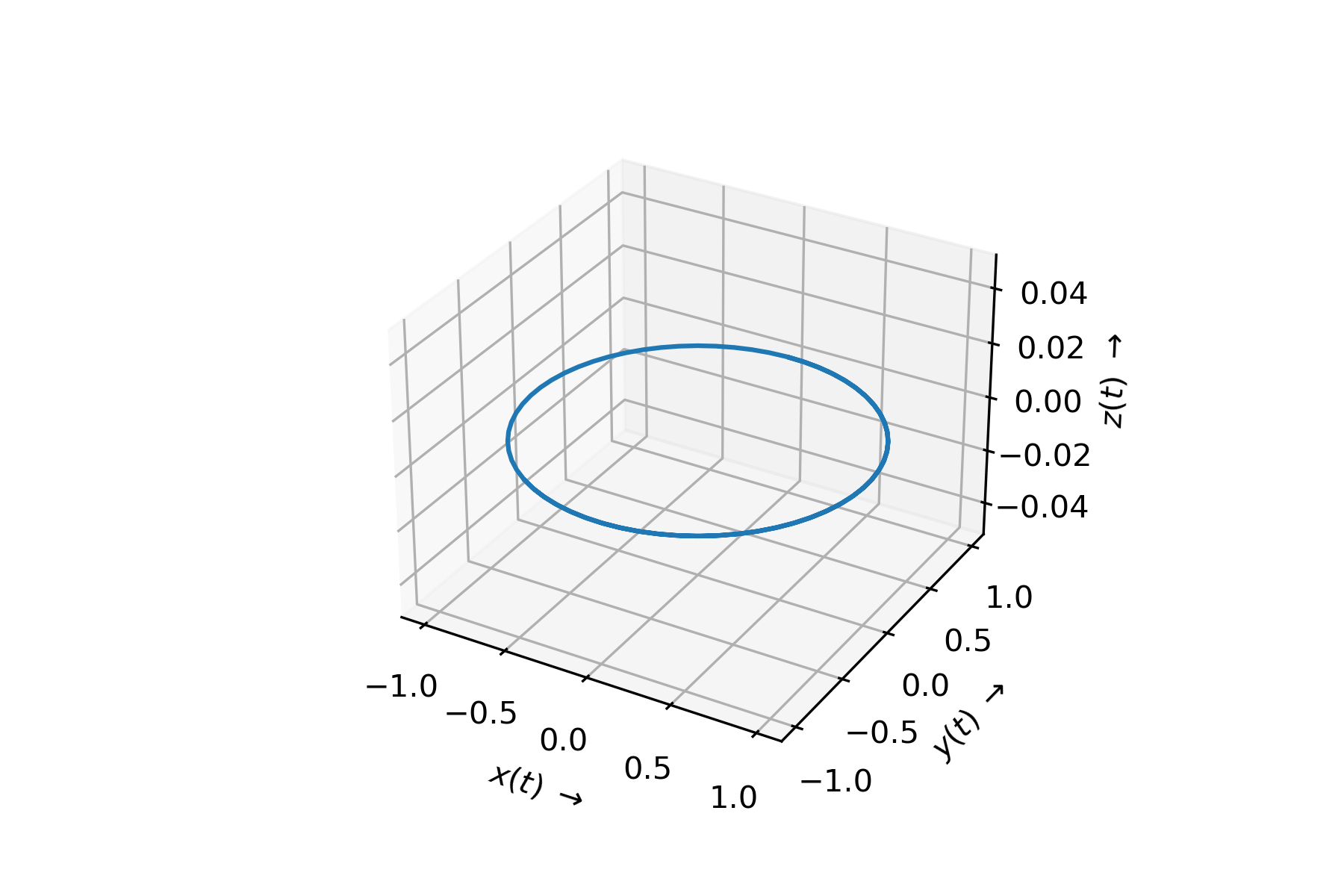
Fig. 2.2 Darstellung einer Bewegung in 2 Dimensionen.

Der einfachste Fall stellt die Bewegung in einer Dimension dar. In diesem Fall bewegt sich der Massenpunkt entlang einer einzigen Raumkoordinate. Die kann zum Beispiel die x-Achse sein, dann findet die Bewegung auf einer Geraden statt.

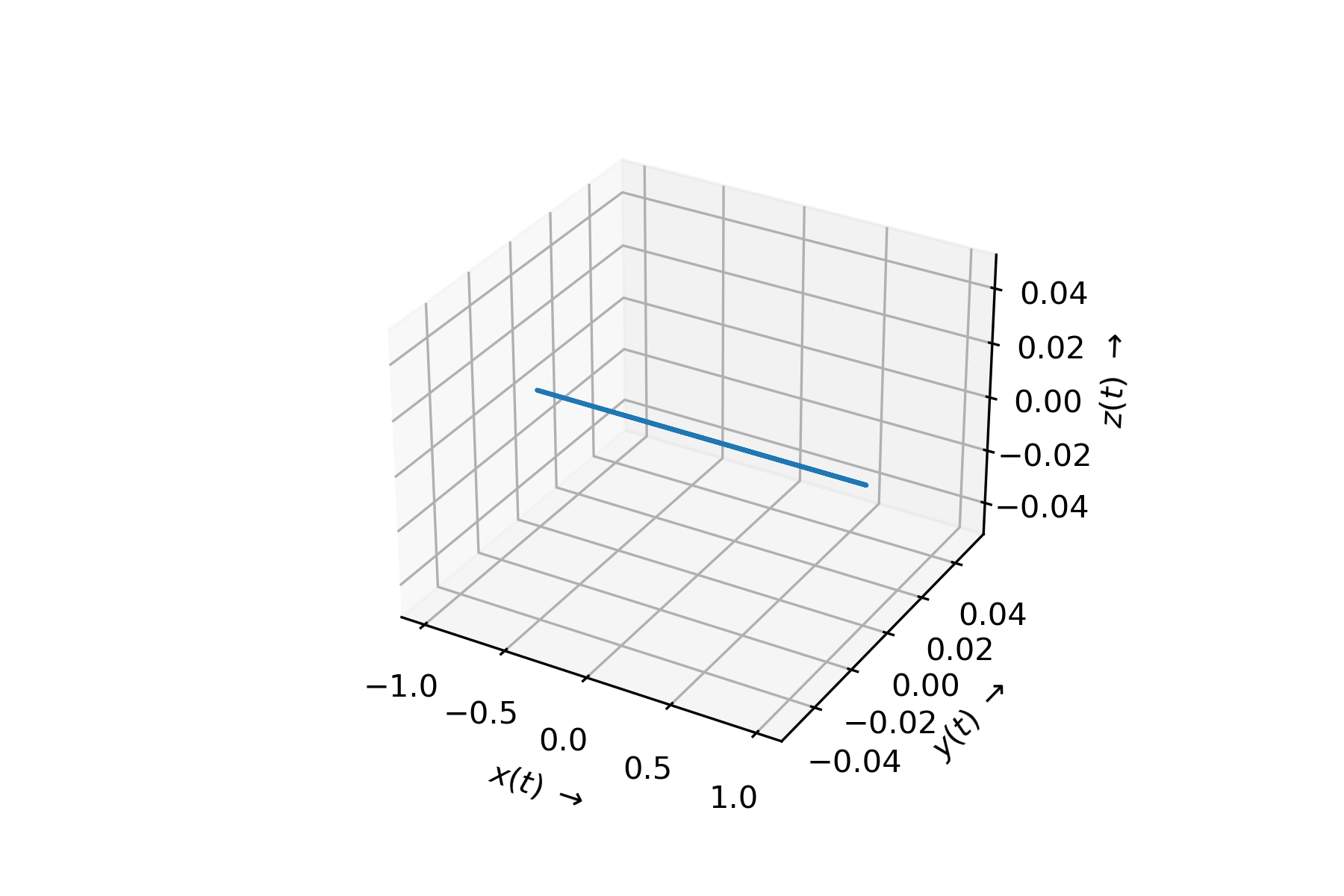
Fig. 2.3 Darstellung einer Bewegung in 1 Dimension.