Beispiele zur eindimensionalen Bewegung eines Massenpunktes

2.3. Beispiele zur eindimensionalen Bewegung eines Massenpunktes#

2.3.1. Beispiel 1: a aus x#

Gegeben sei folgender Zusammenhang zwischen x und t zur Beschreibung der Bewegung eines Massenpunktes

$x(t) = t \cdot \sqrt{t} + 5 t^3$

Wie sehen Geschwindigkeit und Beschleunigung aus?

Lösung:

$x(t) = t \cdot \sqrt{t} + 5 t^3 = t^{3/2} + 5 t^3$

$v(t) = \frac{d}{dt} x(t) = \frac{d}{dt} \left(t^{3/2} + 5 t^3 \right) = \frac{3}{2} t^{1/2} + 5\cdot 3 t^2 = \frac{3}{2} t^{1/2} + 15 t^2$

$a(t) = \frac{d}{dt} \left( \frac{3}{2} t^{1/2} + 15 t^2 \right) = \frac{3}{2} \frac{1}{2}t^{-1/2} + 2\cdot 15 t = \frac{3}{4} \frac{1}{\sqrt{t}}+ 30 t$

2.3.2. Beispiel 2: x aus a#

Ein Massenpunkt erfährt eine Beschleunigung von

$a = 3 \cdot t$.

Wie lauten die Funktionen für $v(t)$ und $x(t)$? Zu Beginn der Bewegung hat der Massenpunkt eine Geschwindigkeit von

$v(0) = 0$

und

$x(0) = 0$.

Lösung:

$v(t) = \int a(t) \, dt = 3\frac{1}{2} t^2 + v(0) = \frac{3}{2} t^2$

$x(t) = \int v(t) \, dt = \frac{3}{2} \frac{1}{3} t^3 + v(0)\cdot t + x(0) = \frac{1}{2} t^3$

2.3.3. Beispiel 3: freier Fall#

Ein Ball, der als Massenpunkt betrachtet werden kann, fällt aus einer Höhe $h$ zu Boden.

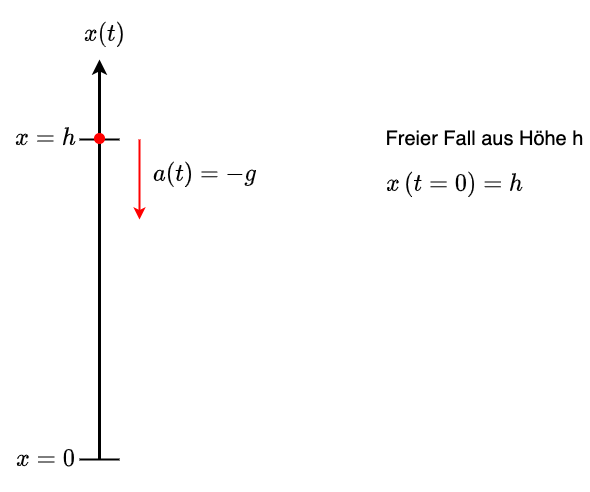
../../../_images/freier_fall.png — Fig. 2.8 Darstellung des freien Falls.#

Nach welcher Zeit erreicht der Ball die Erdoberfläche?
Wie ändert sich die Situation, wenn die Richtung des gewählten Koordinatensystems umgekehrt wird und der Nullpunkt an den Start gesetzt wird?
Wie ändert sich die Situation, wenn der Ball mit $v_0 = 2 \frac{m}{s}$aus einer Höhe von $h= 10 \, m$ nach oben geworfen wird?
Nach welcher Zeit erreicht der Ball den oberen Umkehrpunkt und in welcher Höhe ist dieser?

Lösung:

Im freien Fall wirkt auf einen Massenpunkt (in Oberflächennähe) die konstante Ergbeschleunigung $a = -g$. Die Geschwindigkeit ist demnach

$v(t) = -g \cdot t + v_0$

Wird der Ball in Höhe $h$ losgelassen, ist in diesem Punkt die Geschwindigkeit $v(t = 0) = v_0 = 0$. Damit wird

$v(t) = -g \cdot t$

Für die Position gilt

$x(t) = - \frac{1}{2} g t^2 + x_0$

wobei $x_0$ die Anfangshöhe h ist. Somit gilt

$x(t) = - \frac{1}{2} g t^2 + h$

Kommt der Ball an der Erdoberfläche an, ist $x(t_e) = 0$. Damit ist die dazugehörende Zeit

$x(t_e) = - \frac{1}{2} g t_e^2 + h = 0 \Leftrightarrow \frac{1}{2} g t_e^2 = h \Leftrightarrow t_e = \sqrt{\frac{2h}{g}}$

Wird die Richtung des gewählten Koordinatensystems umgekehrt und der Nullpunkt an den Start gesetzt, ergibt sich folgendes Bild

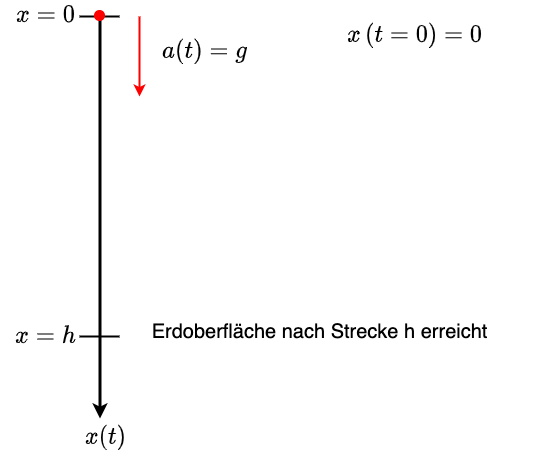
../../../_images/freier_fall_2.png — Fig. 2.9 Darstellung des freien Falls.#

$a = g$

$v(t) = g \cdot t$

$x(t) = \frac{1}{2} g t^2$

und

$x(t_e) = h$

Damit ergibt sich

$h = \frac{1}{2} g t^2 \Leftrightarrow t_e = \sqrt{\frac{2h}{g}}$

Wenn der Ball mit $v_0 = 2 \frac{m}{s}$ aus einer Höhe von $h= 10 \, m$ nach oben geworfen wird, gibt es zum Zeitpunkt $t=0$ eine Anfangsgeschwindigkeit, die der Beschleunigung entgegen gesetzt wird. Beim unsprünglichen Koordinatensystem bedeutet dies

$v(t) = -g \cdot t + v_0$

$x(t) = - \frac{1}{2} g t^2 + v_0\cdot t + h$

Damit wird

$x(t_e) = 0 = - \frac{1}{2} g t^2 + v_0\cdot t + h \Leftrightarrow t^2 = t^2 - \frac{2 \cdot v_0}{g} \cdot t - \frac{2 \cdot h}{g} = 0$

Dies ergibt (mit Hilfe quadratischer Ergänzung / pq-Formel)

$t_e = \frac{v_0}{g} \pm \sqrt{\left(\frac{v_0}{g} + \frac{2 \cdot h}{g}\right)}$

wobei die positive Wurzel die einzig physikalisch sinnvolle Lösung darstellt. Mit $h = 10 m$ und $v_0 = 2 \frac{m}{s}$ ist $t_e = \frac{v_0 = 2 \frac{m}{s}}{g} \pm \sqrt{\left(\frac{v_0 = 2 \frac{m}{s}}{g} + \frac{2 \cdot 10 \, m}{g}\right)} \approx 1.6 \, s$

Am oberen Umkehrpunkt gilt:

$v(t_u) = 0 \Leftrightarrow -g \cdot t_u + v_0 = 0 \Leftrightarrow t_u = \frac{v_0}{g} = 0.2 \, s$

Dies entspricht einer Höhe von

$$x(t_u) = - \frac{1}{2} g t_u^2 + v_0\cdot t_u + h = - \frac{1}{2} g \left(\frac{v_0}{g}\right)^2 + v_0\cdot \frac{v_0}{g} + h = \frac{1}{2} \frac{v_0^2}{g} + h = 10.2 \, m$

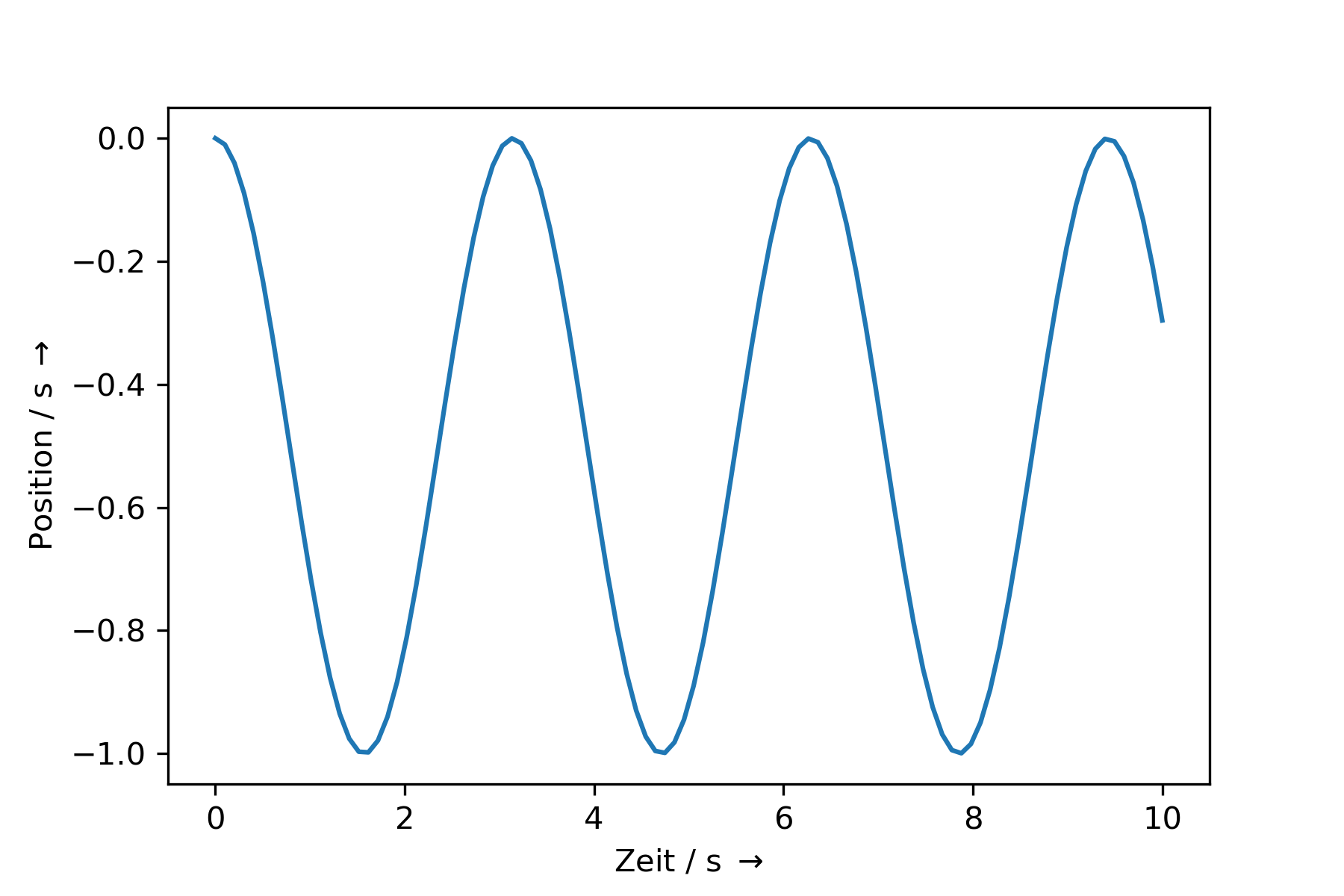
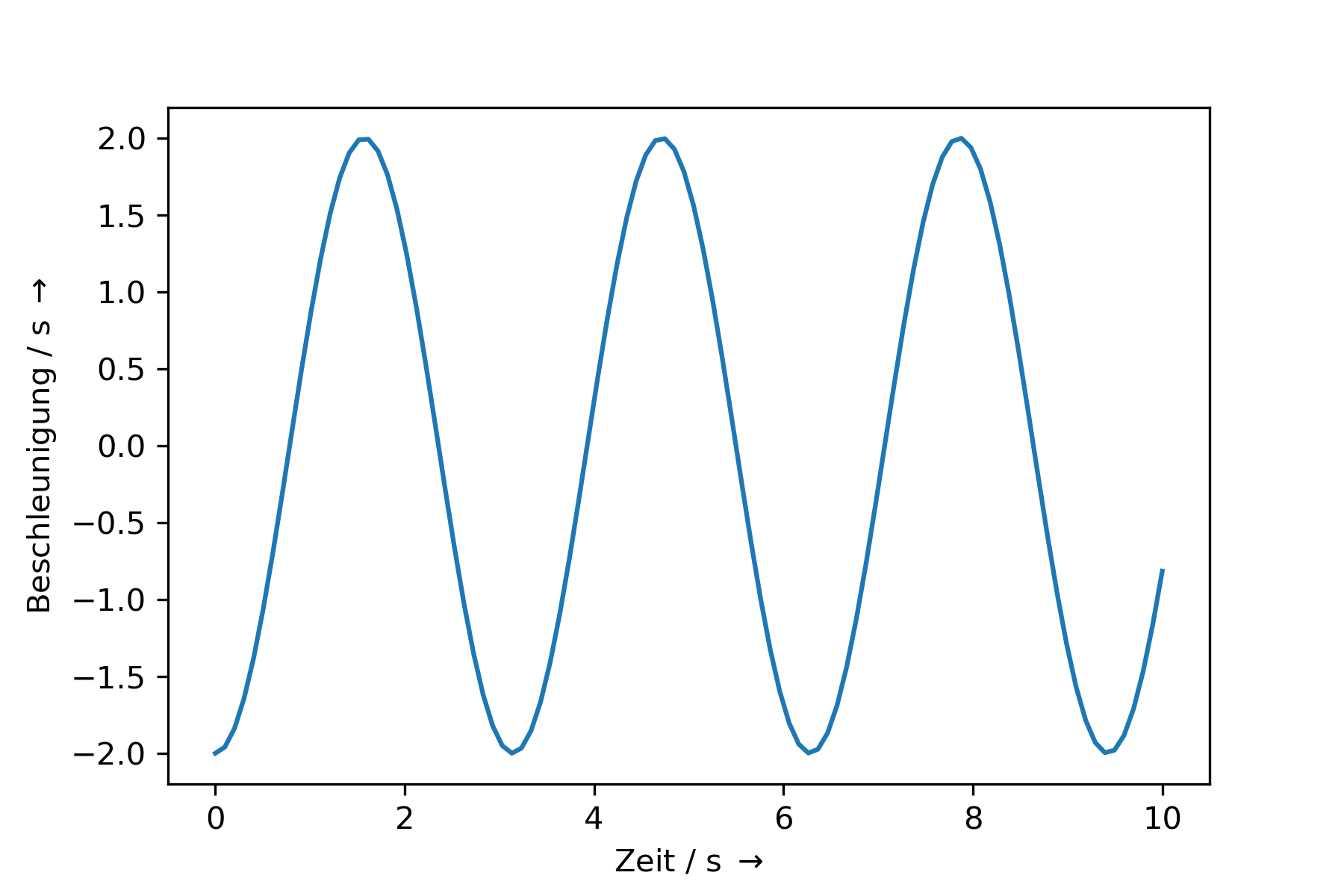
2.3.4. Beispiel 4: Pendel#

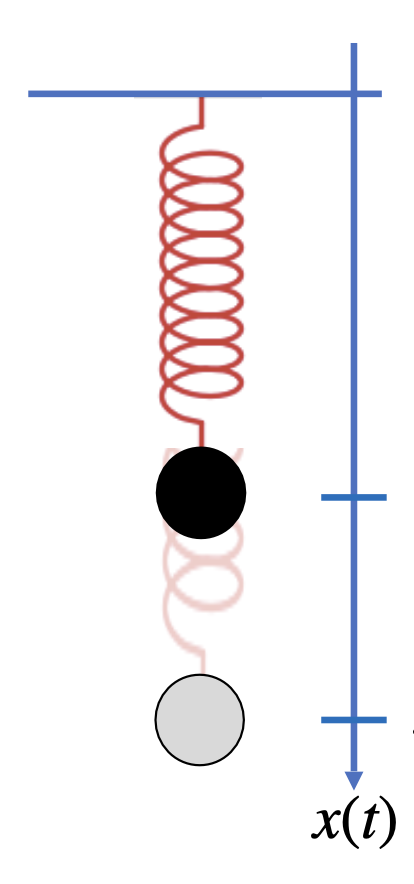
../../../_images/pendel.png — Fig. 2.10 Darstellung einer eindimensionalen Bewegung eines Federpendels.#

Ein Federpendel wird beschrieben durch die Bewegungsgleichung

$x(t) = \frac{1}{2} cos \left(2 \cdot t \right) - \frac{1}{2}$

Zu welchen Zeitpunkten ist die Beschleunigung =0?

Lösung:

$x(t) = \frac{1}{2} cos \left(2 \cdot t \right) - \frac{1}{2}$

$v(t) = \frac{d}{dt} \left(\frac{1}{2} cos \left(2 \cdot t \right) - \frac{1}{2} \right) = - 2 \frac{1}{2} sin \left(2 \cdot t \right) = - sin \left(2 \cdot t \right)$

$a(t) = \frac{d}{dt} \left(- sin \left(2 \cdot t \right) \right) = -2 \cdot cos\left(2 \cdot t \right)$