2.2. Eindimensionale Bewegung eines Massenpunktes#
Betrachtet wird nun der einfachste Fall, nämlich die eindimensionale Bewegung eines Massenpunktes und die Beschreibung durch die dazugehörigen Bewegungsgleichungen.
Im Falle der eindimensionalen Bewegung bewegt sich der Massenpunkt entlang einer Achse. Die Bewegungsgleichung beschreibt also die Position des Massenpunktes auf der Achse und reduziert sich somit zu
\(\vec{r}(t) \longrightarrow x(t)\)
Betrachten wir als Beispiel die Bewegung mit der gegebenen Bewegungsgleichung
\(x(t) = t^2\)
Über diese Bewegungsgleichung kann die Position des Massenpunktes zu einem beliebigen Zeitpunkt berechnet werden. Dies kann in einer Wertetabelle dargestellt werden
Zeit t |
Ort x |
|---|---|
0 |
0 |
1 |
1 |
2 |
4 |
3 |
9 |
4 |
16 |
5 |
25 |
6 |
36 |
7 |
49 |
8 |
64 |
9 |
81 |
10 |
100 |
oder auch graphisch

Fig. 2.4 Darstellung einer Bewegung in 1 Dimension.#
In der Kinematik werden zur Darstellung Weg-Zeit Diagramme verwendet. Dabei wird auf der x-Achse die Zeit und auf der y-Achse die zurückgelegte Strecke aufgetragen. Entsprechend werden diese Diagramme auch als x-t-Diagramm bezeichnet (siehe Abbildung 2.5).
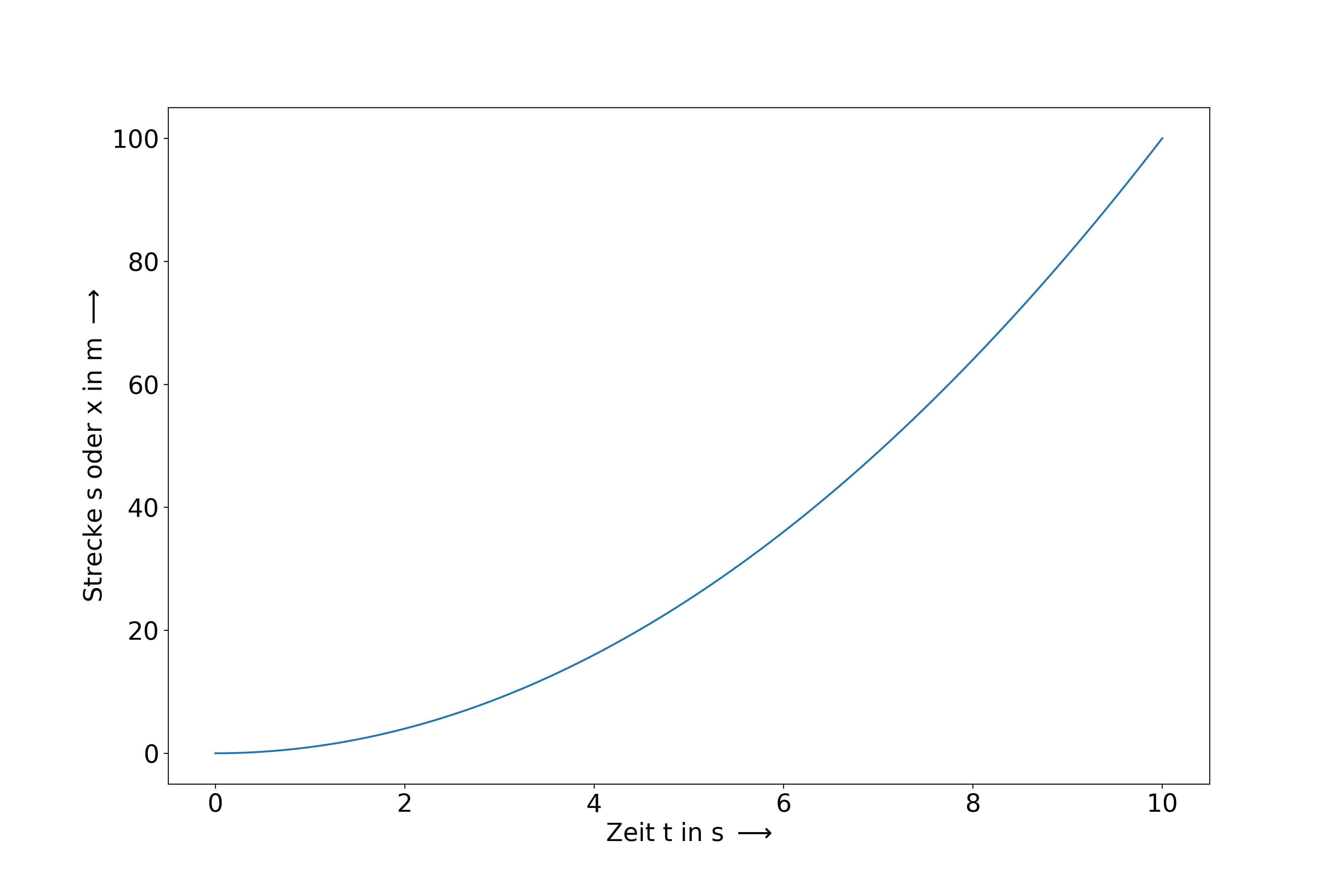
Fig. 2.5 Darstellung einer Bewegung in 1 Dimension.#
Die Geschwindigkeit, mit der sich der Massenpunkt bewegt, lässt sich aus dem funktionalen Zusammenhang aus x und t berechnen. Die Geschwindigkeit ist definiert als die zeitliche Änderung der Position des Massenpunktes und somit
\(v(t) = \frac{dx}{dt} = \dot{x}(t)\)
Der Ausdruck \(\dot{x}(t)\) beschreibt, dass es sich um eine Ableitung nach der Zeit handelt. Im konkreten Beispiel mit \(x(t) = t^2\) gilt somit für die Geschwindigkeit
\(v(t) = \frac{dx}{dt} = \frac{d t^2}{dt} = 2 t\)
Während sich die Position des Massenpunktes quadratisch mit der Zeit ändert, ändert sich die Geschwindigkeit also linear.
Das zugehörige Diagramm wird als v-t-Diagramm bezeichnet. Dabei wird auf der x-Achse die Zeit und auf der y-Achse die Geschwindigkeit aufgetragen (siehe Abbildung 2.6).

Fig. 2.6 Darstellung der Geschwindigkeit einer Bewegung in 1 Dimension.#
Die Beschleunigung, die auf diesen Massenpunkt wirkt, die zeitliche Änderung der Geschwindigkeit. Damit gilt in gleicher Weise
\(a(t) = \frac{dv}{dt} = \dot{v}(t) = \ddot{x}(t)\)
Im konkreten Beispiel mit \(x(t) = t^2\) gilt somit für die Beschleunigung
\(a(t) = \frac{dv}{dt} = \frac{d (2t) }{dt} = 2\)
Die Beschleunigung ist also in diesem Beispiel konstant.
Das zugehörige Diagramm wird als a-t-Diagramm bezeichnet. Dabei wird auf der x-Achse die Zeit und auf der y-Achse die Beschleunigung aufgetragen (siehe Abbildung 2.7).

Fig. 2.7 Darstellung der Beschleunigung einer Bewegung in 1 Dimension.#
2.2.1. Spezialfälle#
Einfache Spezialfälle sind die gleichförmige Bewegung und die gleichmäßig beschleunigte Bewegung
2.2.2. gleichförmige Bewegung#
Die gleichförmige Bewegung ist diejenige Bewegung die auftritt, wenn die wirkende Beschleunigung =0 ist. Dies bedeutet
\(a (t) = 0\)
\(v (t) = v_0 = \) konstant
\(x (t) = v_0 \cdot t\)
Die Geschwindigkeit ist also konstant und Strecke und Zeit hängen linear über die konstante Geschwindigkeit zusammen. Nur in diesem Fall gilt \(v = \frac{s}{t}\).
2.2.3. gleichmäßig beschleunigte Bewegung#
Die gleichmäßig beschleunigte Bewegung tritt auf, wenn die wirkende Beschleunigung konstant ist. Dies bedeutet
\(a (t) = a\)
\(v (t) = a \cdot t + v_0\)
\(x (t) = \frac{1}{2} \cdot a \cdot t^2 + v_0 \cdot t + x_0 \)
Im Fall der gleichmäßig beschleunigten Bewegung gilt dann bei vernachlässigbarer Anfangsgeschwindigkeit \(a =\frac{v}{t}\). Die Strecke hängt quadratisch von der Zeit ab. Diese Art der Bewegung tritt beispielsweise beim freien Fall auf. Hier wirkt die konstante Erdbeschleunigung \(g=9.81 \, \frac{m}{s^2}\).
