6. Temperatureffekte auf Gase#
Bei Gasen ist die mittlere kinetische Energie der Teilchen so hoch, dass die mittleren Abstände zwischen den Teilchen so groß werden, dass elektromagnetische Wechselwirkungen nur eine untergeordnete Rolle spielen. Die Teilchen wechselwirken haupsichtlich durch Stoßprozesse.
Gase nehmen das ihnen zur Verfügung stehende Volumen ein. Im Gegensatz zu Flüssigkeiten sind sie leicht kompressibel.
Bei Temperaturerhöhung nimmt die mittlere kinetische Energie und damit die Geschwindigkeit der Teilchen weiter zu. Nun gibt es zwei Möglichkeiten
Ist das Gas in einem konstanten Volumen eingeschlossen, kann eine Temperaturerhöhung nicht zu einer Volumenausdehnung führen. In diesem Fall steigt der Gasdruck entsprechend \(\Delta p = \gamma \cdot \Delta T \cdot p \left( T_0\right)\).
Ist der Druck des Gases konstant, führt eine Temperaturerhöhung zu einer Volumenausdehnung mit \(V \left(T_0 + \Delta T \right) = V \left(T_0 \right) \left( 1+ \gamma \cdot \Delta T \right)\).
Da bei Gasen die Teilchen hauptsächlich durch Stoßprozesse wechselwirken, ist der Wärmeausdehnungskoeffizient von Gas ist guter Näherung nicht materialabhängig. Allerdings ist er stark temperaturabhängig (siehe Abbildung 6.9)

Fig. 6.9 Räumliche Ausdehnung von Stoffen Von Frank Klemm#
Bei \(0^\circ \,C\) ist er
\(\gamma_{Gas} (0^\circ C )\approx (273,15)^{-1} \frac{1}{K}\)
Da \(\gamma_{Gas}\) stark temperaturabhängig ist, ist es sinnvoll nach einem weiteren physikalischen Zusammenhang zu suchen.
Bei Gasen gibt es somit drei Parameter, die miteinander zusammenhängen: Temperatur, Druck und Volumen. Um das Verhalten von Gasen zu verstehen, ist es sinnvoll zunächst einige Parameter konstant zu lassen und die Abhängigkeit der verbleibenden Parameter zu bestimmen. Dann können diese Erkenntnisse kombiniert und daraus der Zusammenhang zwischen Temperatur, Druck und Volumen ermittelt werden.
6.1. Gesetz von Gay-Lussac#
Zunächst soll der Druck des betrachteten Gases konstant gehalten werden. Dies kann beispielsweise durch die in Abbildung 6.10 dargestellte Anordnung erreicht werden.
Fig. 6.10 Volumenmessung eines Gases bei konstantem Aussendruck#
In Abbildung 6.10 ist ein Glasröhrchen mit einem Gasvolumen gefüllt. Damit das Gas nicht entweichen kann, ist das Röhrchen mit einem Quecksilbertropfen verschlossen. Dieser Tropfen ist jedoch beweglich, so dass eine Volumenausdehnung dazu führt, dass sich der Tropfen nach oben bewegt, eine Volumenverringerung führt zu einer Abwärtsbewegung. Das Gewicht des Quecksilbertropfens und der konstante Aussendruck führen zu einem konstanten Gasdruck. Um die Temperatur zu regulieren, ist das Ganze in ein Wasserbad eingelassen.
Verändert man nun die Temperatur, steigt linear dazu auch das Volumen. Bei konstantem Druck (und konstanter Teilchenzahl) gilt also der Zusammenhang
\(\frac{V}{T} = \) konstant
Dies ist auch bekannt als das Gesetz von Gay-Lussac (siehe Abbildung 6.10).
Fig. 6.11 Gesetz von Gay-Lussac Von Johannes Schneider#
Mit Hilfe dieses Diagramms lässt sich auch der absolute Nullpunkt bestimmen, indem die Gerade bis zu \(T=0\) extrapoliert wird. Damit ergibt sich
\(T_0 = = -273.15 ^\circ C\).
Ebenso lässt sich hieraus der Wärmeausdehnungskoeffizient von Gas bei \(0 \, K\) ermitten.
Aus \(\frac{V}{T} = \) konstant folgt \(\frac{V_1}{T_1} = \frac{V_0}{T_0} \Leftrightarrow V_1 T_0 = V_0T_1\)
mit \(V \left(T_1\right) = V \left(T_0 + \Delta T \right) = V \left(T_0 \right) \left( 1+ \gamma \cdot \Delta T \right) = V \left(T_0 \right) \left( 1+ \gamma \cdot \left( T_1 - T_0 \right)\right)\)
\(\Leftrightarrow V_0 \left(1 + \gamma \left(T_1 - T_0 \right) \right) T_0 = V_0T_1 \Leftrightarrow V_0 \gamma_0 T_0 \left(T_1 - T_0 \right) = V_0\left(T_1 - T_0 \right)\)
\(\Leftrightarrow \gamma_0 T_0 = 1 \Leftrightarrow \gamma_0 = \frac{1}{ T_0}\)
Allgemein gilt dann \(\gamma (T) = \frac{1}{T}\)
6.1.1. Beispiel#
Ein Ballon ist mit Luft gefüllt. Durch Sonneneinstrahlung wird er erwärmt und dehnt sich so aus, dass der Druck im Ballon stets gleich dem Umgebungsdruck ist. Wie groß ist das Volumen des erwärmten Ballons, wenn der Ballon bei \(T = 20^\circ C\) ein Volumen von \(5 \, l\) hatte und um \(\Delta T = 10^\circ C\) erwärmt wird?
Da der Druck konstant ist, gilt \(\frac{V}{T} = \) konstant.
\(V_1 = 5 \, l\)
\(T_1 = 20^\circ C + 273.15 = 293.15 K\)
\(T_2 = T_1 + \Delta T = 20^\circ C + 273.15 + 10^\circ C = 303.15 K\)
Damit ist
\(\frac{V_1}{T_1} = \frac{V_2}{T_2} \Leftrightarrow V_2 = V_1 \frac{T_2}{T_1} = 5 \, l \frac{303.15 K}{293.15 K} = 5.17 \, l\)
6.2. Gesetz von Boyle-Mariotte#
Nun wird bei konstanter Temperatur (und konstanter Teilchenzahl) der Zusammenhang zwischen Druck und Volumen untersucht.
Fig. 6.12 Aufbau zur Messung der Volumenänderung bei konstanter Temperatur und variablem Druck.#
Bei konstanter Temperatur und konstanter Teilchenzahl ist bei einem Idealen Gas der Druck umgekehrt proportional zum Volumen, dies bedeutet
\(p\cdot V = \) konstant
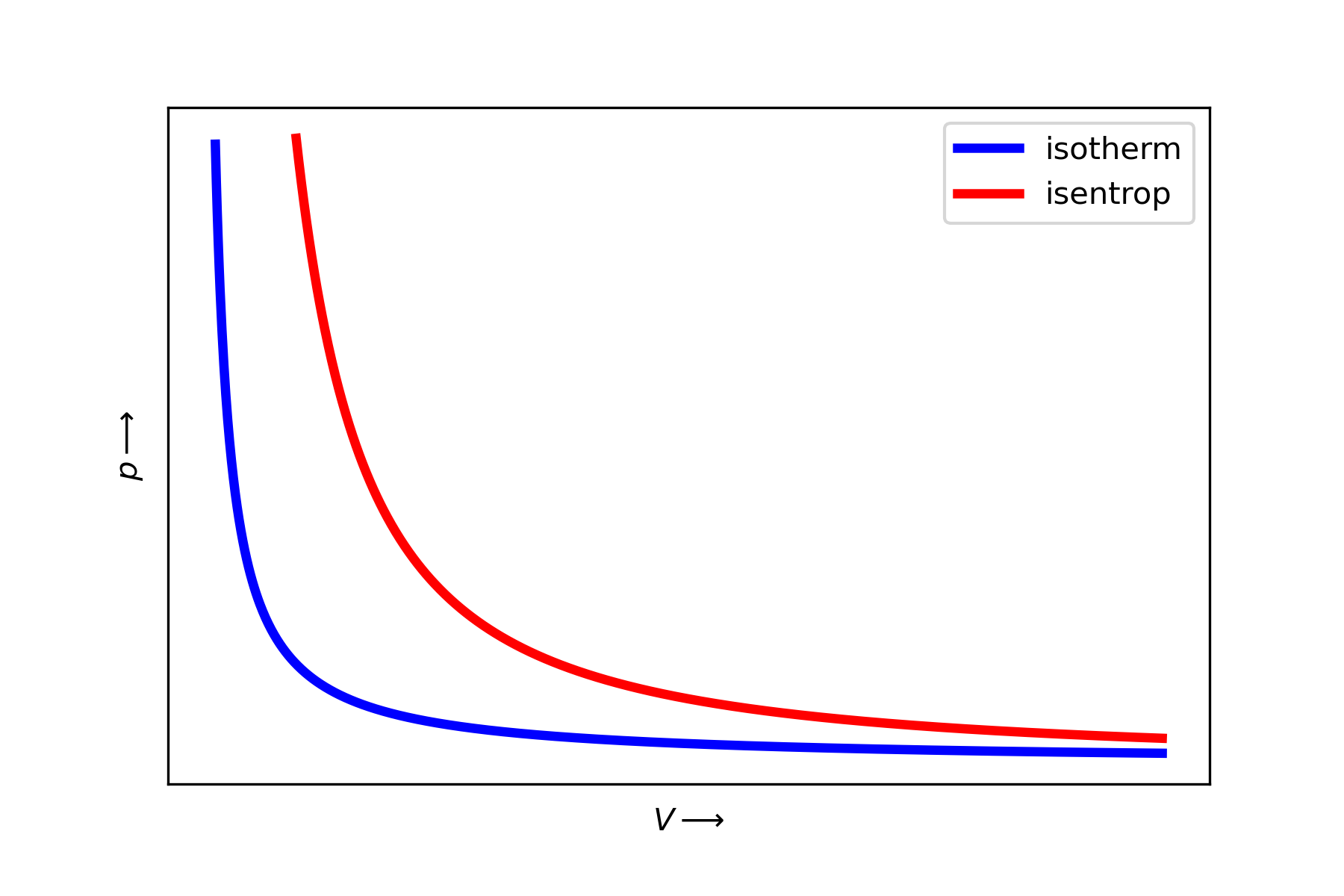
Fig. 6.13 Gesetz von Boyle-Mariotte, \(p\cdot V = \) konstant \(\Rightarrow V \propto \frac{1}{p}\).#
6.2.1. Beispiel: U-Boot#
Ein U-Boot befindet sich im Tauchgang und möchte aufsteigen. Das U-Boot befindet sich in \(20 \, m\) Tiefe. Es hat einen Tank, der zum Abtauchen mit Seewasser gefüllt werden kann, oder zum Auftauchen mithilfe von Pressluft mit Luft gefüllt wird, so dass das Seewasser aus dem Tank verdrängt wird. Da die Temperatur durch das umliegende Wasser vorgegeben wird, und der Prozess hinreichend langsam verläuft, kann \(T = \text{konstant}\) angenommen werden. Die Pressluft hat im Presslufttank einen Druck von \(150 \, bar\) und die Luft, die zum Autauchen benötigt wird hat in der Pressluftflasche ein Volumen von \(50 \, l\). Wie groß ist das Volumen des Seewassers im Tank, welches zum Auftauchen verdrängt wird?
Da \(T = \text{konstant}\) kann das Gesetz von von Boyle-Mariotte angewandt werden.
Damit gilt \(p\cdot V = \) konstant.
Der Druck in der Pressluftflasche ist
\(p_1 = 150 \, bar\)
Der Druck im Tank ist gegeben durch den statischen Druck, bedingt durch die Wassersäule von \(20 \, m\).
\(p_2 = 1 \, bar + \frac{1 \, bar}{10 \, m} \cdot 20 \,m\) = 3 , bar$
In der Pressluftflasche ist das Volumen
\(V_1 = 50 \, l\)
Dann ist mit
\(p_1 \cdot V_1 = p_2 \cdot V_2 \Leftrightarrow V_2 = \frac{p_1}{p_2} \cdot V_1 = \frac{150 \, bar}{3 \, bar} \cdot 50 \, l = 50 \cdot 50 \, l = 2500 \, l = 2.5 \, m^3\)
6.3. Ideales Gasgesetz#
Die Gesetze von Gay-Lussac und Boyle-Mariotte können zu einem Gesetz zusammengebracht werden. Dies ist das ideale Gasgesetz. Das ideale Gasgesetz legt die idealisierte Modellvorstellung eines realen Gases zugrunde, welche nur elastische Stöße zwischen den Teilchen und Teilchen und Wänden betrachtet. Elektrochemischen oder kernphysikalischen Wechselwirkungen verden vernachlässigt. Es kann zur thermodynamischen Beschreibung vieler Prozesse verwendet werden.
Aus \(\frac{V}{T} = \) konstant und \(p\cdot V = \) konstant folgt für ein ideales Gas (mit konstanter Teilchenzahl)
\(\frac{p\cdot V}{T} = \) konstant
Bleibt die Masse eines (idealen) Gases konstant, so ist das Produkt aus Druck und Volumen , geteilt durch die absolute Temperatur, konstant.
Die Konstante konnte zunächst nur experimentell bestimmt werden, später konnte Sie durch die kinetische Gastheorie, also durch statistische Betrachtungen hergeleitet werden.
Dadurch ergibt sich das Allgemeine Gasgesetz
\(p\cdot V = n \cdot R \cdot T\)
mit
\(R = 8.31446261815324 \, \frac{J}{mol\cdot K}\) die Universelle Gaskonstante
\(n = \) Stoffmenge = Anzahl der mol des Stoffen, dabei ist ein mol = \(6.02214076 \cdot 10^{23}\) Teilchen
\(R\) kann auch ausgedrückt werden durch die Avogadro-Konstante \(N_A = 6.02214076 \cdot 10^{23} \frac{1}{mol}\) und die Boltzmann-Konstante \(k_B = 1.380649 \cdot 10^{-23} \frac{J}{K} \) \(\Rightarrow R = k_B \cdot N_A\)
Alternativ zu universellen Gaskonstante \(R\) wird manchmal auch die spezifische Gaskonstante \(R_S\) verwendet, diese ist im Gegensatz zu \(R\) auf die molare Masse \(M = \frac{m}{n}\) des Stoffes bezogen und ist definiert als
\(R_S = \frac{R}{M}\)
Damit ergeben sich folgende alternative Formulierungen des idealen Gasgesetzes:
\(p\cdot V = N \cdot k_B \cdot T\)
mit \(N\) = \(n\cdot N_A\) = Anzahl der Teilchen
oder
\(p\cdot V = m \cdot R_S \cdot T\)
6.3.1. Beispiel: Gasflasche#
In einem Druckflasche mit dem Volumen von \(0,1 \, m^3\) herrscht ein Druck von \(200 \, bar\). Die Temperatur beträgt \(T = 25 ^\circ C\) und der Behälter ist mit Sauerstoff gefüllt. Der Sauerstoff soll näherungsweise als ideales Gas angenommen werden.
Wie viele \(mol\) Sauerstoff sind in der Flasche?
\(p\cdot V = n \cdot R \cdot T \Leftrightarrow n = \frac{p\cdot V}{R \cdot T} = \frac{200 \cdot 10^5 \, Pa \cdot 0,1 \, m^3}{R \cdot (25+273.15) K} \approx 807 \, mol\)
