1.4. Galilei-Transformation

Bei nichtrelativistischen Bewegungen (\(v \ll c\)) beschreibt die Galilei-Transformation den Übergang von einem Bezugssystem zum anderen.

Fig. 1.6 Darstellung einer Koordinatentransformation.

Bei der Galilei-Transformation betrachtet man ein Koordinatensystem \(O\) und ein Koordinatensystem \(O^\prime\), welches sich von \(O\) wegbewegt. Zum Zeitpunkt \(t=0\) liegen die Koordinatenurspünge in den folgenden Betrachtungen übereinander. Prinzipiell können die Koordinatensysteme auch einen Offset haben.

Betrachtet aus \(O\) bewegt sich der Koordinatenursprung von \(O^\prime\) mit \(\frac{1}{2} \vec{a}_{O \rightarrow O^\prime} t^2 + \vec{v}_{0, O \rightarrow O^\prime}t\)

Der Ortsvektor, der die beiden Koordinatenursprünge miteinander verbindet ist demnach

\(\vec{r}_{O \rightarrow O^\prime} = \frac{1}{2} \vec{a}_{O \rightarrow O^\prime} t^2 + \vec{v}_{0, O \rightarrow O^\prime}t\)

Eine Herleitung dieser Zusammenhänge erfolgt im Kapitel Kinematik des Massenpunktes.

Ein Punkt \(P\) wird nun aus beiden Bezugssystemen betrachtet. Im Bezugssystem \(O\) bezeichnet \(\vec{r}\) den Ortsvektor von Koordinatenursprung zum Punkt \(P\). Im Bezugssystem \(^\prime\) bezeichnet \(\vec{r}^\prime\) den Ortsvektor von Koordinatenursprung zum Punkt \(P\) (siehe Abbildung 1.7).

Da der Vektor \(\vec{r}_{O \rightarrow O^\prime}\) die beiden Koordinatenursprünge miteinander verbindet, gilt

\( \vec{r} = \vec{r}^\prime + \vec{r}_{O \rightarrow O^\prime}\)

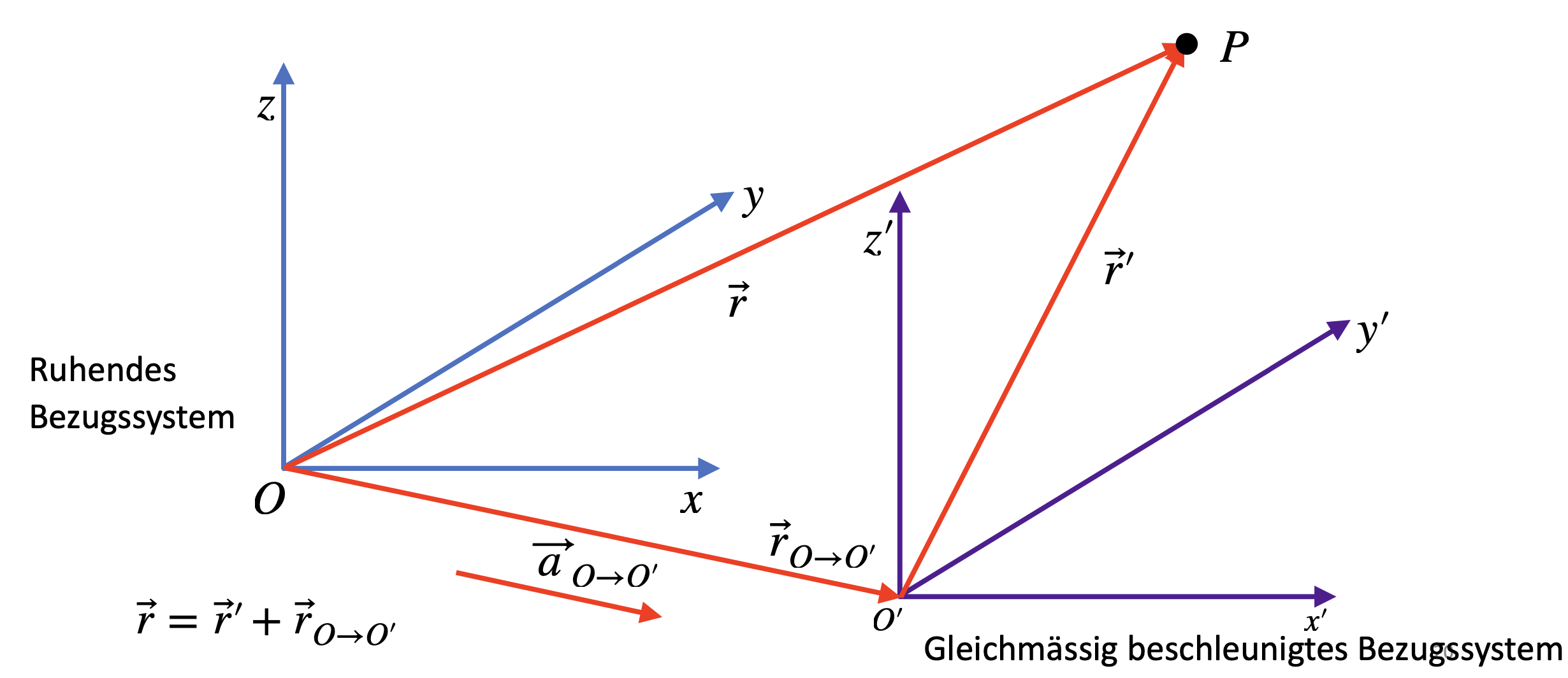
Fig. 1.7 Darstellung der Galilei Koordinatentransformation.

Damit gelten folgende Zusammenhänge

\(O^\prime \rightarrow O\)	\(O \rightarrow O^\prime\)
\( \vec{r} = \vec{r}^\prime + \frac{1}{2} \vec{a}_{O \rightarrow O^\prime} t^2 + \vec{v}_{0, O \rightarrow O^\prime}t\)	\( \vec{r}^\prime = \vec{r} - \frac{1}{2} \vec{a}_{O \rightarrow O^\prime} t^2 - \vec{v}_{0, O \rightarrow O^\prime}t\)
\( \vec{v} = \vec{v}^\prime + \vec{a}_{O \rightarrow O^\prime}t + \vec{v}_{0, O \rightarrow O^\prime}\)	\( \vec{v}^\prime = \vec{v} - \vec{a}_{O \rightarrow O^\prime} t - \vec{v}_{0, O \rightarrow O^\prime}\)
\( \vec{a} = \vec{a}^\prime + \vec{a}_{O \rightarrow O^\prime}\)	\( \vec{a}^\prime = \vec{a} - \vec{a}_{O \rightarrow O^\prime}\)

1.4.1. Spezialfall \(\vec{a}_{O \rightarrow O^\prime} = \vec{0}\)

Bewegt sich \(O^\prime\) mit konstanter Geschwindigkeit von \(O\) weg, ist \(\vec{a}_{O \rightarrow O^\prime}=0\). Diese Bezugssysteme sind die Inertialsysteme. Die Gesetze der klassischen Mechanik sind daher unter Galilei-Transformationen invariant, da sie in ihrer einfachsten Form in Inertialsystemen gelten.

Dann gilt

\(O^\prime \rightarrow O\)	\(O \rightarrow O^\prime\)
\( \vec{r} = \vec{r}^\prime + \vec{v}_{0, O \rightarrow O^\prime}t\)	\( \vec{r}^\prime = \vec{r} - \vec{v}_{0, O \rightarrow O^\prime}t\)
\( \vec{v} = \vec{v}^\prime + \vec{v}_{0, O \rightarrow O^\prime}\)	\( \vec{v}^\prime = \vec{v} - \vec{v}_{0, O \rightarrow O^\prime}\)
\( \vec{a} = \vec{v}^\prime \)	\( \vec{a}^\prime = \vec{a}\)