4. Hydrostatik#
Definition: Der hydrostatische Druck (Gravitationsdruck), ist der Druck, der sich innerhalb eines ruhenden Fluids, das ist eine Flüssigkeit oder ein Gas, durch den Einfluss der Gravitation einstellt. Quantitativ beschrieben wird er durch das Pascal’sche Gesetz.
4.1. Pascal’sches Gesetz#
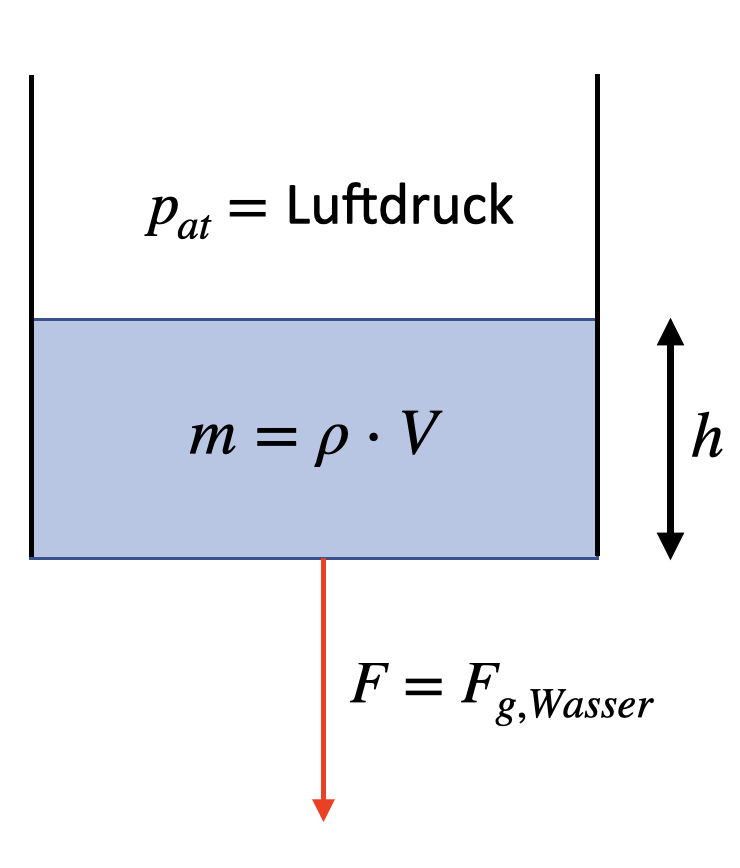
Fig. 4.19 Pascal’sches Gesetz#
Auf die Grundfläche wirkt die Kraft \(F = m \cdot g = \rho \cdot V \cdot g = \rho \cdot h \cdot A \cdot g \)
Der Druck ist definiert als \(p = \frac{F}{A} \)
Der hydrostatische Druck (Schweredruck) in der Tiefe \(h\) ist
\(p_h = \rho \cdot g \cdot h\)
Zusammen mit dem Luftdruck \(p_{at}\) an der Oberfläche ergibt sich der Absolutdruck
\(p = p_{at} + \rho \cdot g \cdot h\)
4.2. Hydrostatisches Paradoxon#
\(p_h\) hängt nicht von der Form eines Gefäßes ab! Entscheidend für den Druck an dessen Boden ist alleine die Höhe des Fluid- bzw. Flüssigkeitsspiegels und dessen Dichte! Grund dafür ist, dass die Gefäßwände Kräfte auf die Flüssigkeit ausüben: Bei schrägen Wänden tragen sie einen Teil des Flüssigkeitsgewichts bzw. drücken zusätzlich nach unten.
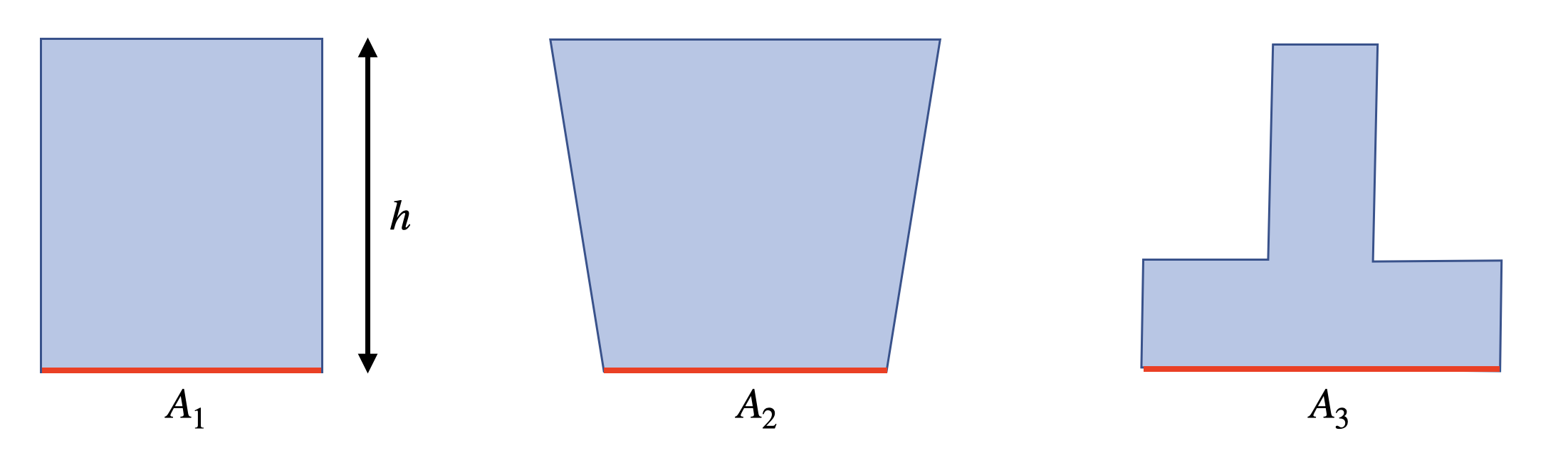
Fig. 4.20 Hydrostatisches Paradoxon#
4.2.1. Anwendung: Kommunizierende Röhren#
Da der Druck entlang der roten Linie gleich ist, ist der Füllstand in allen Röhren gleich, unabhängig von ihrer Form. Gilt für Röhren, die zu breit genug sind, dass der Kapillareffekt keine Rolle spielt
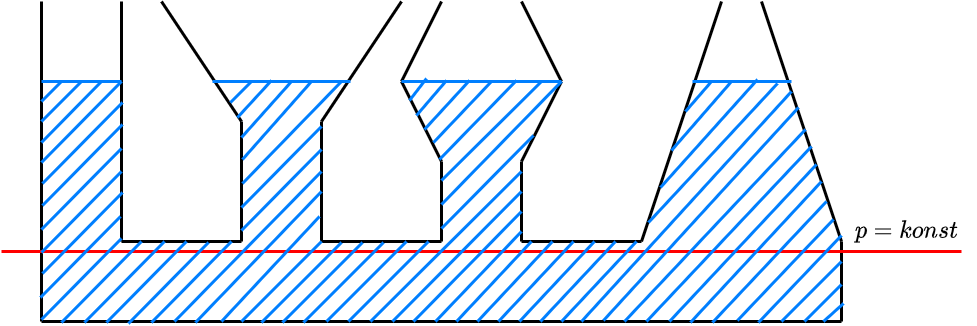
Fig. 4.21 Kommunizierende Röhren#
Dies macht man sich bei der Schlauchwaage zunutze. Eine Schlauchwaage besteht aus zwei Gefäßen mit Maßeinteilungen (meist mm). Die beiden Gefäße sind oben offen und besitzen Bodenöffnungen, durch die sie mit einem Schlauch verbunden sind. Das Gefäß-Schlauchsystem wird mit Wasser gefüllt. Durch den in beiden Gefäßen gleichen Wasserspiegel lassen sich Höhenunterschiede ablesen oder übertragen. Bevor man den Wasserspiegel der Schlauchwaage als Markierung übernimmt, muss der Schlauch unbedingt frei von Luftblasen sein.
4.2.2. Beispiel: Kommunizierende Röhren#
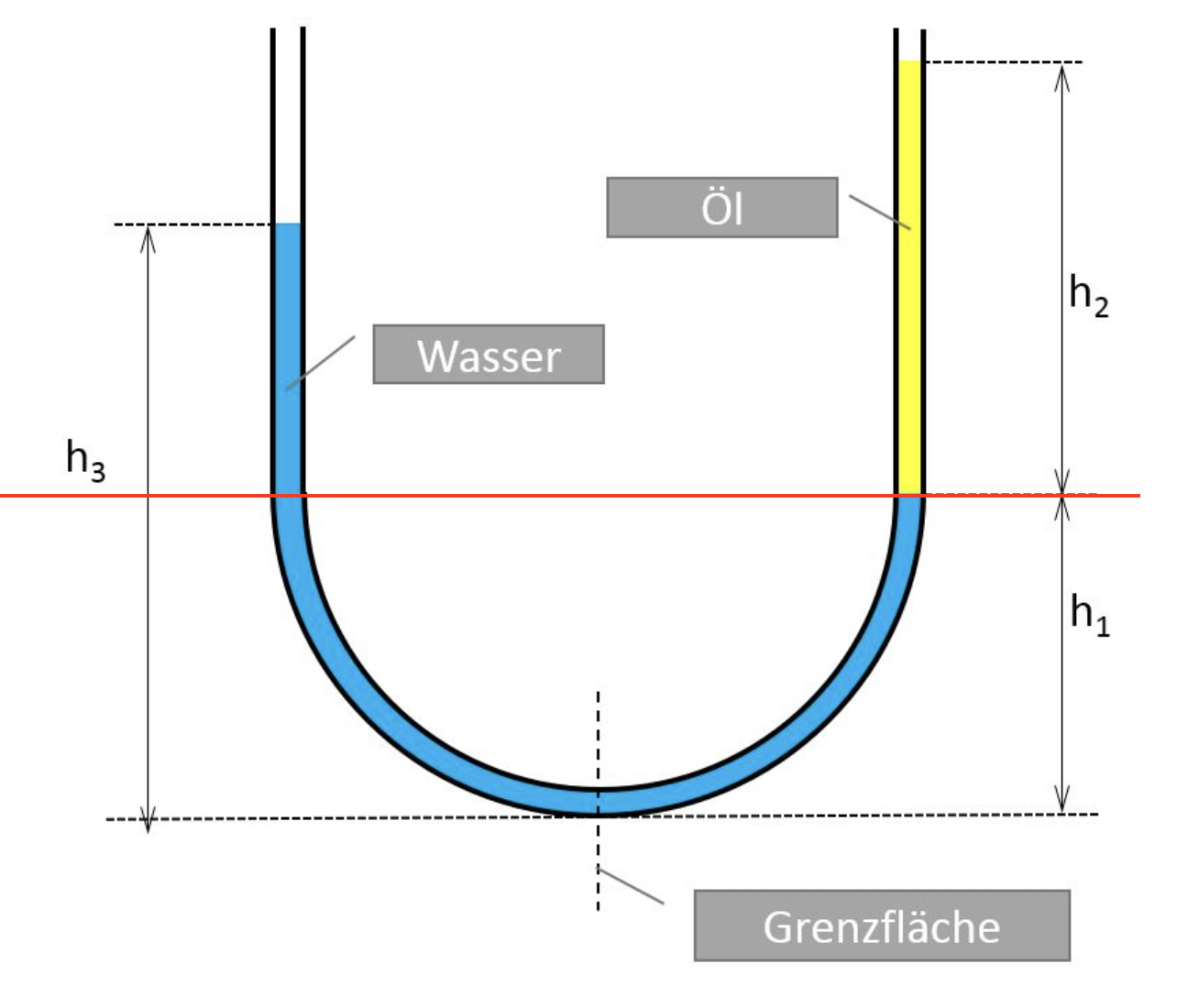
Fig. 4.22 Kommunizierende Röhren#
Bei unterschiedlichen Flüssigkeiten steigt die leichtere Flüssigkeit höher
\(\rho_{Wasser} = \rho_W = 1.00 \, \frac{g}{cm^3}\)
\(\rho_{Oel} = \rho_O= 0.9 \, \frac{g}{cm^3}\)
\(p_{links} = p_{rechts} \Leftrightarrow \rho_W \cdot g \cdot (h_3 - h_1) = \rho_O \cdot g \cdot h_2 \Leftrightarrow h_2 = \frac{\rho_W}{\rho_O} (h_3-h_1)\approx 1.11 \cdot (h_3-h_1)\)
4.3. Auftrieb#
Der (statische) Auftrieb ist das Phänomen, dass ein Körper, der in ein ruhendes Fluid (eine Flüssigkeit oder ein Gas) eintaucht, scheinbar an Gewicht verliert. Seine Gewichtskraft wird teilweise, vollständig oder überschießend durch die statische Auftriebskraft kompensiert.
\(F_A = \rho \cdot g \cdot V_{verdraengt}\)
Beschrieben wird das Phänomen des Auftriebs durch das Archimedische Prinzip:
Der statische Auftrieb eines Körpers in einem Medium ist genauso groß wie die Gewichtskraft des vom Körper verdrängten Mediums.
Fig. 4.23 Prinzip des Auftriebs#
\(F_l\) und \(F_r\) heben sich auf.
\(F_o\) und \(F_u\) sind entgegengerichtet. Insgesamt wirkt die Kraft
\(F_o + F_u = - \rho \cdot g \cdot h_0 \cdot A + \rho \cdot g \cdot (h_0 + h) \cdot A = \rho \cdot g \cdot h \cdot A = \) Auftriebskraft, wobei \(\rho\) die Dichte des den Körper umgebenden Mediums ist.
Damit ist die Auftriebskraft
\(F_A = \rho \cdot g \cdot V\)
Ist \(F_G < F_A \longrightarrow\) steigt der Körper auf
Ist \(F_G = F_A \longrightarrow\) schwebt der Körper
Ist \(F_G > F_A \longrightarrow\) sinkt der Körper ab
4.3.1. Beispiel: Schwimmender Eisberg#
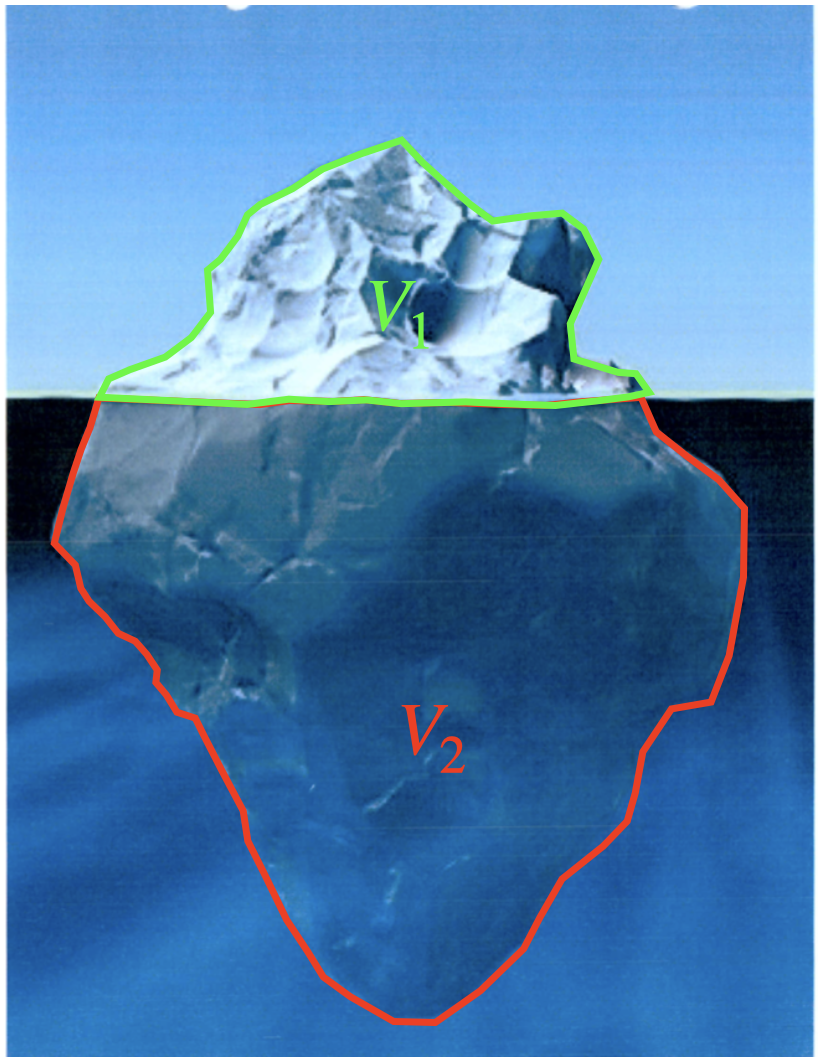
Fig. 4.24 Schwimmender Eisberg#
Dichte des Wassers: \(\rho_W = 1.02 \frac{g}{cm^3}\)
Dichte des Eises: \(\rho_{Eis} = 0.92 \frac{g}{cm^3}\) bei \(-20^\circ C\)
Dichte Eis inkl. Luftblasen: \(\rho_{Eis,L} = 0.84 \frac{g}{cm^3}\)
Eisberg schwimmt \(\Rightarrow F_G = F_A\)
\(F_G = m_E \cdot g = \rho_{Eis,L} \left(V_1 + V_2 \right) \cdot g\)
\(F_A = \rho_W \cdot V_2 \cdot g\)
\(F_G = F_A \Leftrightarrow \rho_{Eis,L} \left(V_1 + V_2 \right) \cdot g = \rho_W \cdot V_2 \cdot g\)
\(\Leftrightarrow \rho_{Eis,L} \cdot V_1 + \rho_{Eis,L} \cdot V_2 = \rho_W \cdot V_2\)
\(\Leftrightarrow V_1 = \frac{\rho_W - \rho_{Eis,L}}{\rho_{Eis,L}} V_2 \Rightarrow \frac{V_1}{V_2} = \frac{\rho_W - \rho_{Eis,L}}{\rho_{Eis,L}} \approx 0.214 \approx \frac{1}{5}\)