6.4. Raketengleichung#
Mit Hilfe der Gesetze von Energie- und Impulserhaltung lassen sich nun die Bewegunggleichungen einer Rakete herleiten.
Hierzu gelten folgende Annahmen:
gesucht wir dieBewegungsgleichung einer sonst kräftefreien (idealisierten) Rakete
Die Beschleunigung wird durch einen kontinuierlichen Ausstoß des Treibstoffs erzeugt (konstanter Massenstrtom)
möglicher Luftwiderstand wird vernachlässigt
Für Kraft und Impuls gilt dadurch der Zusammenhang
\(\vec{F} = \frac{d \vec{p}}{dt} = \frac{d}{dt} \left( m \cdot \vec{v}\right)\)
Da das System abgeschlossen und kräftefrei ist, gilt
\(\frac{d\vec{p}}{dt} = 0\)
Da der Impuls über den Ausstoß von Treibstoff erzeugt wird, ändert sich die Masse der Rakete und es gilt
\(\frac{d}{dt}m = \dot{m} \neq 0\)
Das Koordinatensystem wird so gewählt, dass die Bewegung im momentanen Schwerpunktsystem der Rakete betrachtet wird.
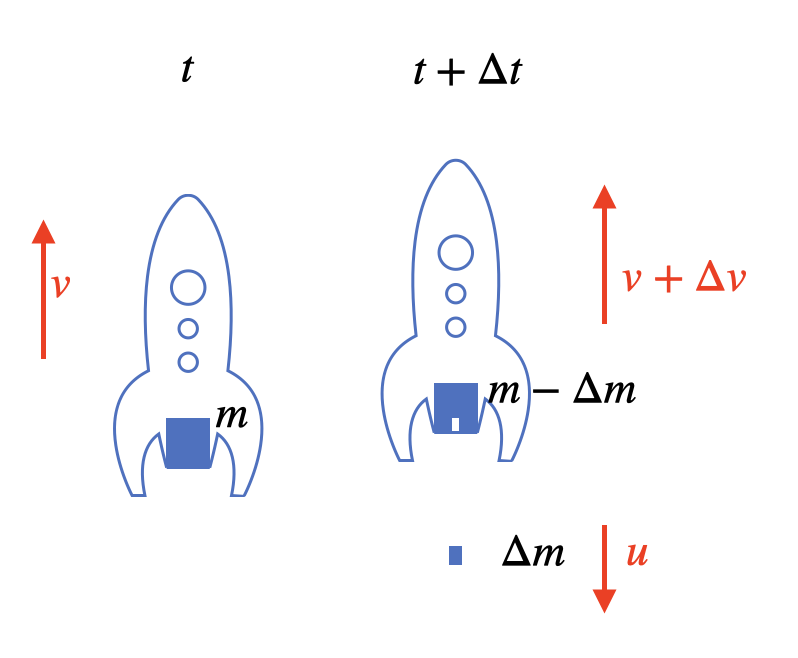
Fig. 6.7 Darstellung des Raketenantriebs#
Die Beschleunigung der Rakete, also die Impulsänderung der Rakete, wird durch Treibstoffausstoß hervorgerufen (siehe Abbildung 6.7 ). Zwischen einem Zeitpunkt \(t\) und \(\Delta t\) wird ein Treibstoffelement \(\Delta m\) ausgestoßen. Das ausgestoßene Treibstoffelement bewegt sich mit der Geschwindigkeit \(u\) nach unten, die Rakete mit \(v + \Delta v\) nach oben.
\(\Delta p = \Delta p_{Rakete} = p(t+\Delta t) -p(t) = \left(\left(m - \Delta m \right) \cdot \left(v + \Delta v \right) + \Delta m\cdot u\right) - m\cdot v = m \Delta v + m v_{rel} \)
mit \(v_{rel} = - \left( v+\Delta v-u \right)\)
Da der Treibstoffausstoff kontinuerlich vonstatten geht, geht man zu infinitesimal kleinen Zeitschritten und Treibstoffelementen über.
\(\Delta t \rightarrow dt \Rightarrow \frac{dp}{dt} = m\cdot \frac{dv}{dt} + \frac{dm}{dt}\cdot v_{rel}\)
Da eine (von äußeren) Kräften freie Rakete betrachtet wird, ist \(= F_{aussen} =:0\) und somit
\(F_{aussen} = \frac{dp}{dt} = 0 = m\cdot \frac{dv}{dt} + \frac{dm}{dt}\cdot v_{rel}\)
Damit ergibt sich folgende zu lösende (Differential-) Gleichung:
\(m\cdot \frac{dv}{dt} = - \dot{m}\cdot v_{rel} = - \mu \cdot v_{rel}\)
mit dem konstanten Massenstrom \(\mu = \dot{m}\).
Die Lösung der dieser Gleichung ist \(v(t) = -v_{rel} \cdot ln (m(t)) + C\)
Beweis
\(\frac{d v(t)}{dt} = -v_{rel} \frac{d}{dt} ln \left( m(t) \right) + \frac{d C}{dt} = -v_{rel} \frac{1}{m(t)} \frac{d m(t)}{dt} = -v_{rel}\frac{\dot{m(t)}}{m(t)} \)
Die Integrationskonstante lässt sich durch die Anfangsbedingung bestimmen. Für den Zeitpunkt \(t=0\) gilt:
\(v (t=0) = 0 \) mit \(m (t=0) = m_0\)
\(\Rightarrow 0 = - v_{rel} \cdot ln \left( m_0 \right) + C \Leftrightarrow C = v_{rel}\cdot ln \left( m_0 \right)\)
Damit gilt für die Rakete
\(v(t) = - v_{rel} \cdot \left( ln \left( \dot{m} \right) - ln \left( m_0 \right) \right) \Leftrightarrow v(t) = v_{rel} \left( ln \left( \frac{1}{\dot{m}} \right) +ln \left( m_0 \right) \right) \Leftrightarrow v(t) = v_{rel} \cdot ln \left( \frac{m_0}{m(t)} \right)\)
Die Masse der Rakete setzt sich zusammen aus ihrer Eigenmasse und der Treibstoffmasse. Ist der Treibstoff leer gilt \(m(t) = m_R\) und die Rakete hat ihre Endgeschwindigkeit erreicht
\(\Rightarrow v_{end} = v_{rel} \cdot ln \left(\frac{m_R + m_T}{m_R} \right) \Leftrightarrow v_{end} = v_{rel} \cdot ln \left( 1 + \frac{m_T}{m_R} \right)\)
