4.2. Kreisbewegungen#
Ist die statische Bedingung nicht erfüllt, gibt es ein resultierendes Drehmoment, welches \(\not = 0\) ist. Das resultierende Drehmoment führt dann zu einer Drehbewegung. Dies wird im Folgenden am Beispiel eines Massenpunktes betrachtet.
Ein Massenpunkt sei an einer festen Drehachse der Länge \(l\) drehbar gelagert (Abbildung 4.6).
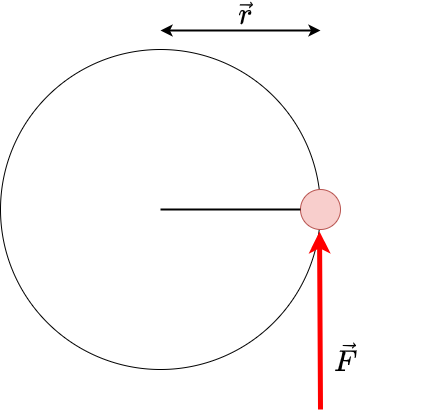
Fig. 4.6 Kreisbewegung eines Massenpunktes.#
Die am Massenpunkt angreifende Kraft \(\vec{F}\) erzeugt ein Drehmoment
\(\vec{M} = \vec{r} \times \vec{F}\)
Zwischen \(\vec{F}\) und \(\vec{r}\) ist ein Winkel von \(90^\circ\), sodass gilt
\(M = m \cdot a \cdot r\)
Gesucht ist nun eine Bewegungsgleichung, die die Bewegung des Massenpunktes beschreibt.
Da es sich um eine Kreisbewegung mit konstanten Radius handelt, kann das Problem durch die Verwendung von Polarkoordinaten (siehe Polarkoordinaten) auf ein eindimensionales Problem reduziert werden. Zwischen kartesischen Koordinaten und Polarkoordinaten gilt der Zusammenhang
\( \vec{r} = \left(\begin{array}{c} x \\ y \end{array}\right) \longrightarrow \left(\begin{array}{c} r \cdot cos \left( \phi \right) \\ r \cdot sin \left( \phi \right) \end{array}\right) \)
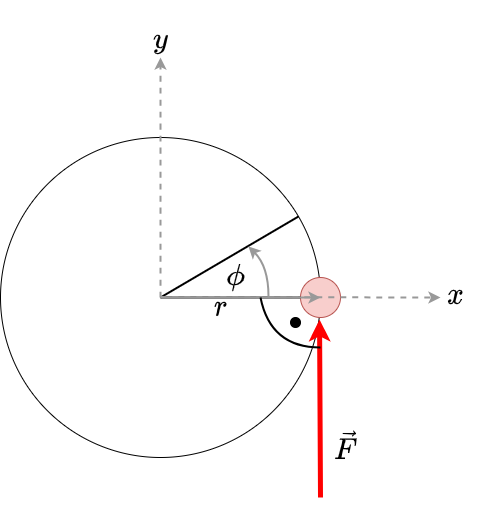
Fig. 4.7 Kreisbewegung eines Massenpunktes in Polarkoordinaten.#
Da \(r\) konstant ist, ist die Variable, die die Bewegung beschreibt, der Winkel \(\phi\). Der Massenpunkt bewegt sich auf dem Kreisbogen und legt auf diesem eine Strecke \(s\) zurück. Es gilt der Zusammenhang
\(s(t) = r \cdot \phi(t)\)
Die Geschwindigkeit, mir der sich der Massenpunkt auf der Kreisbahn bewegt, hängt über die zeitliche Ableitung mit der zurückgelegten Strecke zusammen.
\(v(t) = \dot{s} = \frac{ds(t)}{dt} = r \cdot \frac{d \phi(t)}{dt}\)
da \(r\) konstant ist. Die Ableitung \(\frac{d \phi(t)}{dt}\) wird auch als Winkelgeschwindigkeit \(\omega\) bezeichnet.
\(v(t) = r \cdot \omega (t) \)
Oft wird bei Kreisbewegungen die Drehzahl \(N\) angegeben. Diese beschreibt die Anzahl der Umdrehungen pro Minute und hängt mir der Winkelgeschwindigkeit zusammen über
\( \omega = 2 \cdot \pi \cdot \frac{N}{60}\)
Die Beschleunigung auf der Kreisbahn ist die Ableitung der Geschwindigkeit, also
\(a(t) = \dot{v} = \frac{d^2s(t)}{dt^2} = r \cdot \frac{d^2 \phi(t)}{dt^2} = r \cdot \frac{d \omega(t)}{dt}\)
da \(r\) konstant ist. Die Ableitung \(\frac{d \omega(t)}{dt}\) wird auch als Winkelgeschwindigkeit \(\alpha\) bezeichnet.
\(a(t) = r \cdot \alpha (t) \)
4.2.1. Spezialfall: \(\alpha = 0\)#
Ist die Winkelbeschleunigung \(\alpha = 0\) resultieren daraus die Bewegungsgleichungen
\(\alpha (t) = 0\)
\(\omega (t) = \int \alpha = \omega_0\)
\(\phi (t) = \int \omega = \omega_0 \cdot t + \phi_0\)
Die resultierende Kreisbewegung ist also eine Kreisbewegung mit konstanter Geschwindigkeit
Beispiel:
4.2.2. Spezialfall: \(\alpha = \) konstant#
Ist die Winkelbeschleunigung \(\alpha = 0\) resultieren daraus die Bewegungsgleichungen
\(\alpha (t) = 0\)
\(\omega = \int \alpha = \omega_0\)
\(\phi = \int \omega = \omega_0 \cdot t + \phi_0\)
Beispiel:
4.2.3. Gegenüberstellung der Bewegungsgleichungen bei Translation und Rotation#
Translation |
Rotation |
||
|---|---|---|---|
keine Beschleunigung |
\(a(t)=0\) |
keine Winkelbeschleunigung |
\(\alpha (t)= 0\) |
\(v(t) = v_0\) |
\(\omega (t) = \omega_0\) |
||
\(x(t) = v_0 \cdot t + x_0 \) |
\(\phi (t) = \omega_0\cdot t + \phi_0\) |
||
konstante Beschleunigung |
\(a(t) = a\) |
konstante Winkelbeschleunigung |
\(\alpha (t) = \alpha\) |
\(v(t) = a\cdot t + v_0\) |
\(\omega (t) = \alpha \cdot t + \omega_0\) |
||
\(x(t) = \frac{1}{2} a \cdot t^2 + v_0 \cdot t + x_0 \) |
\(\phi (t) = \frac{1}{2} \alpha \cdot t^2 + \omega_0\cdot t + \phi_0\) |
