9. Thermodynamische Zustandsänderungen#
Im Folgenden werden die vier grundlegenden Zustandsänderungen genauer analysiert. Mit Hilfe dieser grundlegenden Zustandsänderungen könnnen viele Thermodynamische Prozesse in sogenannte Vergleichsprozesse übersetzt und damit berechenbar gemacht werden.
Zuvor seien noch einmal die wichtigsten für nachfolgende Betrachtungen notwengigen Gleichungen wiederholt:
Wärmekapazitäten:
\(C_V = \left(\frac{dU}{dT} \right)_{V = \text{konst.}}\Leftrightarrow dU = C_V \cdot dT |_{V = \text{konst.}}= m \cdot c_V \cdot dT |_{V = \text{konst.}}\)
\(C_p = \left(\frac{dH}{dT} \right)_{p = \text{konst.}}\Leftrightarrow dH = C_p \cdot dT |_{p = \text{konst.}}= m \cdot c_p \cdot dT |_{p = \text{konst.}}\)
Enthalpie: \(H = U + p \cdot V \)
\(\Rightarrow dH = dU + p \cdot dV + V \cdot dp \Leftrightarrow dU + V \cdot dp = dH - p \cdot dV\)
Innere Energie:
\(\Delta U = \Delta Q + \Delta W = \Delta Q + \Delta W_{diss} + \Delta W_{V}\)
Allgemeine Gasgleichung:
\(p\cdot V = n \cdot R \cdot T = N \cdot k_B \cdot T = m \cdot R_S \cdot T\)
Bei thermodynamischen Prozessen bzw. Zustandsänderungen wird Arbeit verrichtet. Der Begriff der Arbeit wurde im Kapitel zur Energie erläutert. Bei thermodynamischen Zustandsänderungen ist dies eine Volumenänderungsarbeit, dies ist die Arbeit, die verrichtet wird, um eine Volumenänderung durch Kompression zu erzeugen. Diese ist
\(W_{V,12} = \int_1^2 F \cdot ds = \int_1^2 p \cdot A \cdot ds = \int_1^2 p \cdot dV\)
Unterschieden werden vier grundlegende Zustandsänderungen, die Isochore, die Isobare, die Isotherme und die Adiabate, bzw. Isentrope. Diese werden nun einzeln betrachtet und erläutert.
Wichtiges Hilfsmittel zur Betrachtung thermodynamischer Zustandsänderungen sind \(p-V\)-Diagramme und \(T-S\)-Diagramme.
Beim \(p-V\)-Diagramm wird der Druck gegenüber dem Volumen aufgetragen, beim \(T-S\)-Diagramm die Temperatur gegenüber der Entropie. Mit diesen Diagrammen lassen sich thermodynamische Zustandsänderungen beschreiben und vergleichen.
9.1. Isochore Zustandsänderung#
Bei der isochoren Zustandsänderung (kurz: Isochore) wird eine Zustandsänderung betrachtet, die bei konstantem Volumen erfolgt.
\(\Rightarrow V = \) konstant
Dies wird im Folgenden anhand der Wärmezufuhr bei konstantem Volumen betrachtet, analog in umgekehrter Richtung verläuft die Wärmeabfuhr bei konstantem Volumen.
Die Wärmezufuhr bei konstantem Volumen ist in Abbildung 9.1 dargestellt, hier ist \(V_1 = V_2\)
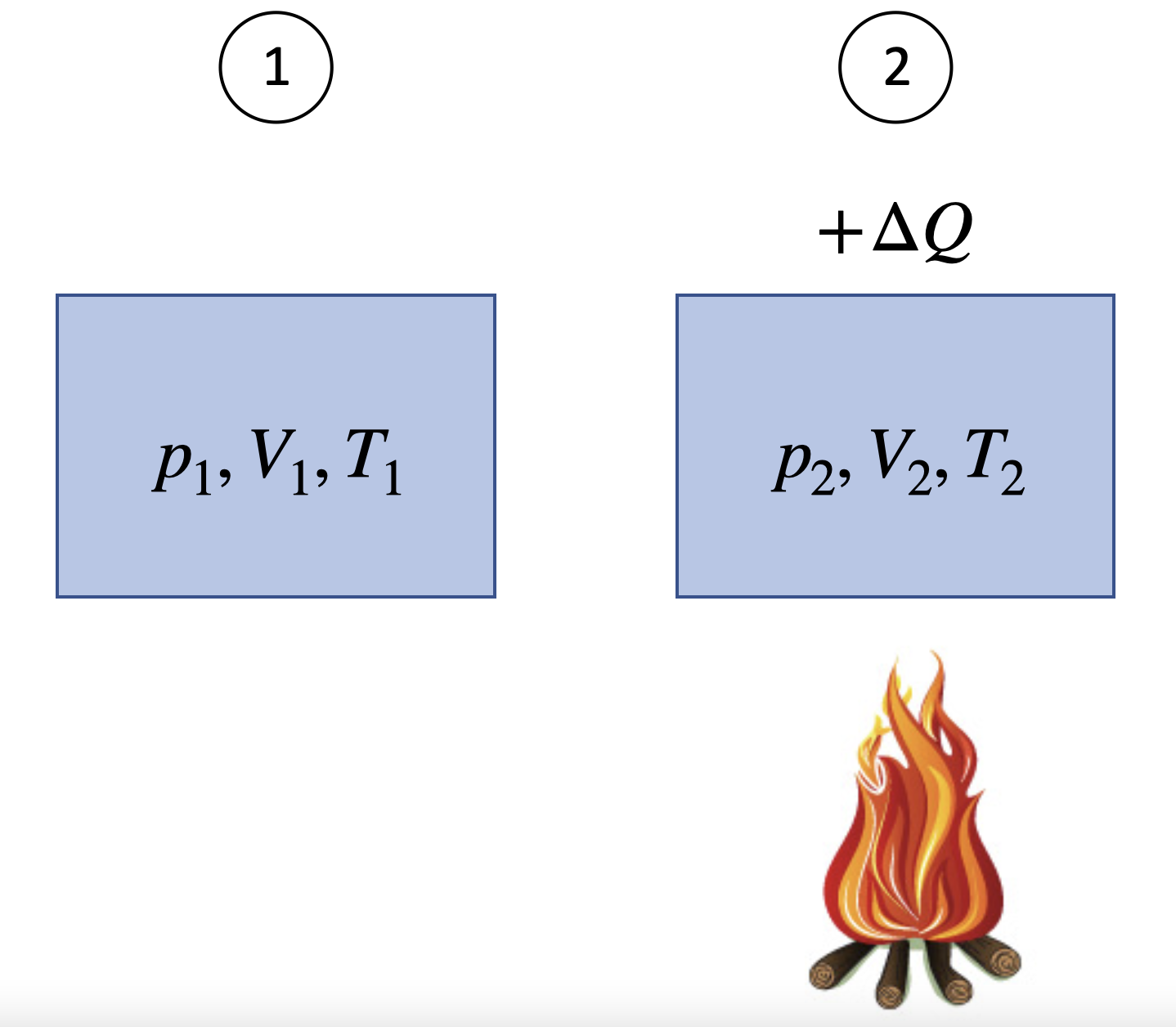
Fig. 9.1 Wärmezufuhr bei konstantem Volumen#
Aus der allgemeinen Gasgleichung folgt
\(p \cdot V = n \cdot R \cdot T \Leftrightarrow \frac{p \cdot V}{T} = n \cdot R = \text{konst.} \Rightarrow \frac{p_1 \cdot V_1}{T_1} = \frac{p_2 \cdot V_2}{T_2} \)
Da das Volumen per Definition konstant bleibt, gilt
\(V_1 = V_2 = V \Rightarrow \frac{p_1}{T_1} = \frac{p_2}{T_2}\), so dass \(T_2 > T_1 \Rightarrow p_2 > p_1\).
In diesem Prozess ändert sich die innere Energie des Systems, da Wärme hinzugefügt wird.
\(\Delta U = \Delta Q + \Delta W \)
Da das Volumen konstant bleibt, ist \(\Delta W = 0\) und somit \(\Delta U = \Delta Q\).
Die hinzugefügte Wärmemänge kann über die Temperaturänderung und die Wärmekapazität ermittelt werden. Da \(V = \) konstant, muss natürlich die Wärmekapazität bei konstantem Volumen betrachtet werden.
\(C_V = \left( \frac{dU}{dT}\right)_{V=\text{konst.}} \Rightarrow dU = C_V \cdot dT = m \cdot c_V \cdot dT |_{V=\text{konst.}} = dQ \Rightarrow \Delta Q = m \cdot c_V \cdot \Delta T |_{V=\text{konst.}} \)
Das zugehörige \(p-V\)-Diagramm sieht daher wie folgt aus:
Fig. 9.2 \(p-V\)-Diagramm der isochoren Zustandsänderung#
Für einen reibungsfreien Prozess ist die Änderung der Entropie: \(dS = \frac{d Q}{T} + \frac{dW_{diss}}{T} = \frac{d Q}{T}\)
Mit \(\Delta U = \Delta Q \Rightarrow \)dU = dQ$ ist
\(\Rightarrow dS = \frac{dQ}{T} = \frac{dU}{T} = m \cdot c_V \cdot \frac{dT}{T}\)
Wenn \(c_V = \text{konst.}\) folgt daraus
\(S = m \cdot c_V \cdot ln \left(T \right)= m \cdot ln \left(T^{c_V} \right) \Rightarrow T \propto \sqrt[c_V]{e^S}\)
Das zugehörige \(T-S\)-Diagramm sieht daher wie folgt aus:
Fig. 9.3 \(T-S\)-Diagramm der isochoren Zustandsänderung#
9.1.1. Beispiel: Mit Luft gefüllte Flasche#
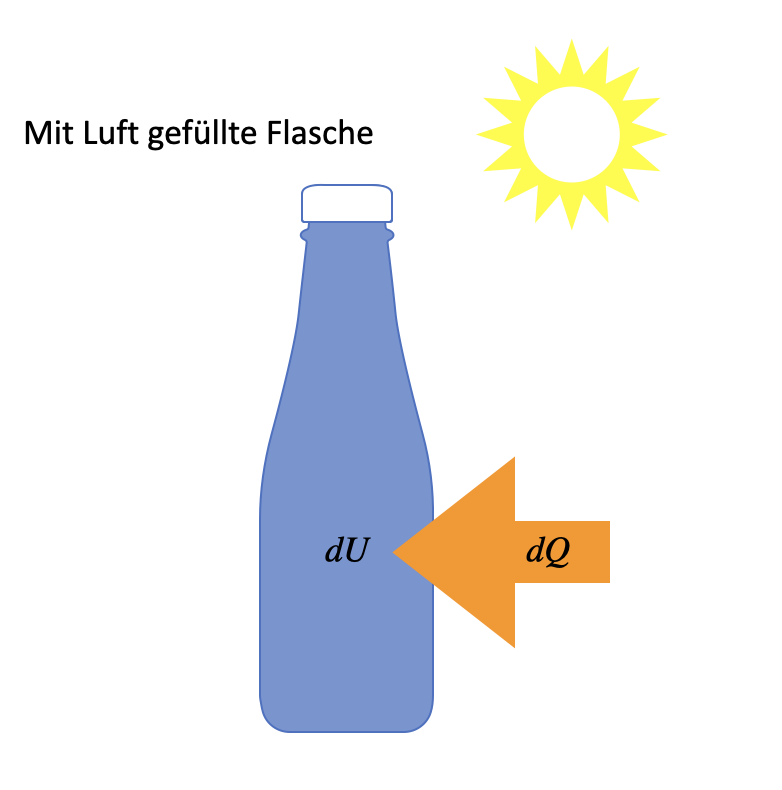
Fig. 9.4 Beispiel für eine isochore Zustandsänderung#
Sonne scheint auf eine mit Luft gefüllte Flasche, die sich nicht ausdehnen kann. Die Sonne fügt der Luft eine bestimmte Wärmemenge \(\Delta W\) hinzu.
Damit ändert sich die innere Energie entsprechen der Isochoren
\(\Delta U = \Delta Q = c_V \cdot m \cdot \Delta T\)
Aus der idealen Gasgleichung folgt
\(\frac{p}{T} = \text{konst.} = \frac{p_{vorher}}{T_{vorher}} = \frac{p_{nachher}}{T_{nachher}}\)
und somit
\(\Delta Q = c_V \cdot m \cdot \Delta T = c_V \cdot m \cdot T_{vorher} \left(\frac{p_{nachher}}{p_{vorher}} -1 \right) \)
Damit kann nun aus den Druck in der Flasche zu Beginn der Zustandsänderung und der Temperaturdifferenz, der Druck in der Flasche am Ende der Zustandsänderung berechnet werden.
9.2. Isobare Zustandsänderung#
Bei der isobaren Zustandsänderung (kurz: Isobare) wird eine Zustandsänderung betrachtet, die bei konstantem Druck erfolgt. Dies ist derselbe Prozess, der bei der Ermittlung des Gesetzes von Gay-Lussac verwendet wurde.
\(\Rightarrow p = \) konstant
Dies wird im Folgenden anhand der Wärmezufuhr bei konstantem Druck betrachtet, analog in umgekehrter Richtung verläuft die Wärmeabfuhr bei konstantem Druck.
Die Wärmezufuhr bei konstantem Druck ist in Abbildung 9.5 dargestellt, hier ist \(p_1 = p_2\)
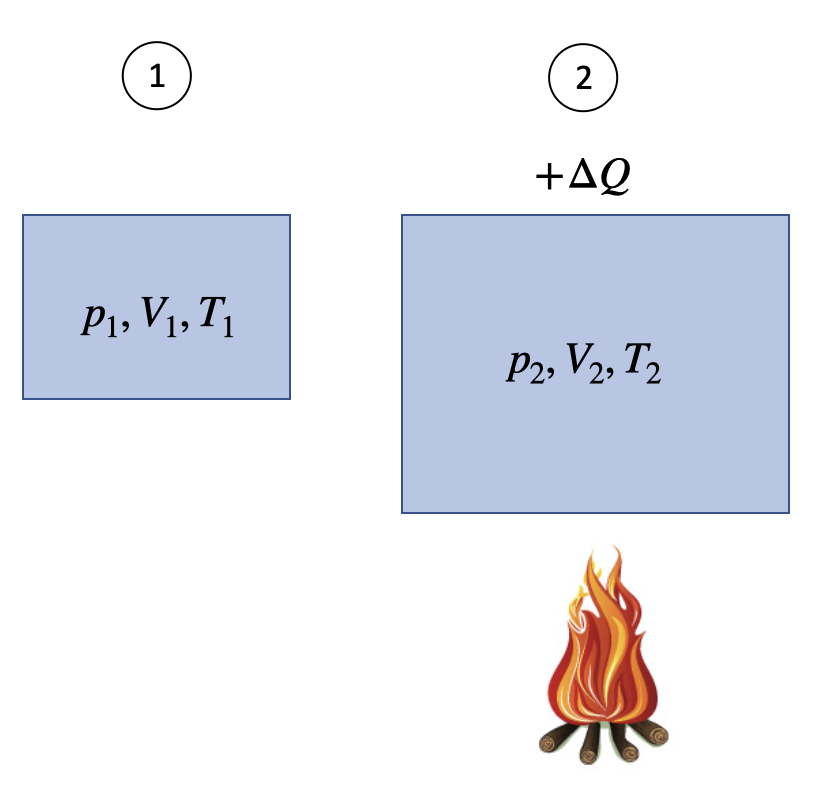
Fig. 9.5 Wärmezufuhr bei konstantem Druck#
Da \(p = \) konstant ist, folgt aus dem idealen Gasgesetz
\(\frac{V_1}{T_1} = \frac{V_2}{T_2}\)
und somit
\(T_2 > T_1 \Rightarrow V_2 > V_1\)
Das zugehörige \(p-V\)-Diagramm sieht daher wie folgt aus:
Fig. 9.6 \(p-V\)-Diagramm der isobaren Zustandsänderung#
Die mit der \(V\) -Achse eingeschlossene Fläche entspricht der Volumenänderungsarbeit.
Fig. 9.7 \(p-V\)-Diagramm der isobaren Zustandsänderung#
Da in diesem Fall Volumenänderungsarbeit verrichtet wird gilt:
\(dU = dQ + dW = dQ - p\cdot dV\)
Anmerkung \(dW = -p \cdot dV\), da das Gas Volumenänderungsarbeit am System verrichtet.
\(dU = dQ + dW = dQ - p\cdot dV \Leftrightarrow dQ = dU + p \cdot dV = m \cdot c_V \cdot dT + p \cdot dV\)
Änderung der Entropie \(dS\) ist für einen reibungsfreien Prozess: \(dS = \frac{d Q}{T} + \frac{dW_{diss}}{T} = \frac{d Q}{T}\)
Mit \(H = U + p\cdot V = \) ist die Änderung der Enthalpie \(dH\)
\(dH = dU + p\cdot dV + V \cdot dp \Leftrightarrow dH - V \cdot dp = dU + p\cdot dV\)
mit \(dU = dQ + dW = dQ - p\cdot dV \Leftrightarrow dQ = dU + pdV\)
ist dann \(dQ = dH - V dp = dH\), da \(dp = 0\) (Druck konstant!)
Für die Änderung der Entropie ist dann
\(dS = \frac{d Q}{T} = \frac{dH}{T} \)
Dies entspricht bei konstantem Druck gerade der Definition der Wärmekapazität bei konstantem Druck
\(\frac{dH}{T} = \left| \frac{C_p \cdot dT }{T} \right| _{p = \text{konst.}} = m \cdot c_p \frac{dT}{T}\)
Somit ergibt sich der Zusammenhang bei konstantem \(c_p\)
\(S = m \cdot c_p \cdot ln \left(T \right) = m \cdot ln \left(T^{c_p} \right) \Rightarrow T \propto \sqrt[c_p]{e^S}\)
Dies bedeutet das der Verlauf der Isobaren \(T-S\) -Diagramm flacher ist, als der der Isochoren.
Fig. 9.8 \(T-S\)-Diagramm der isobaren Zustandsänderung#
9.2.1. Beispiel: Hubkolben#
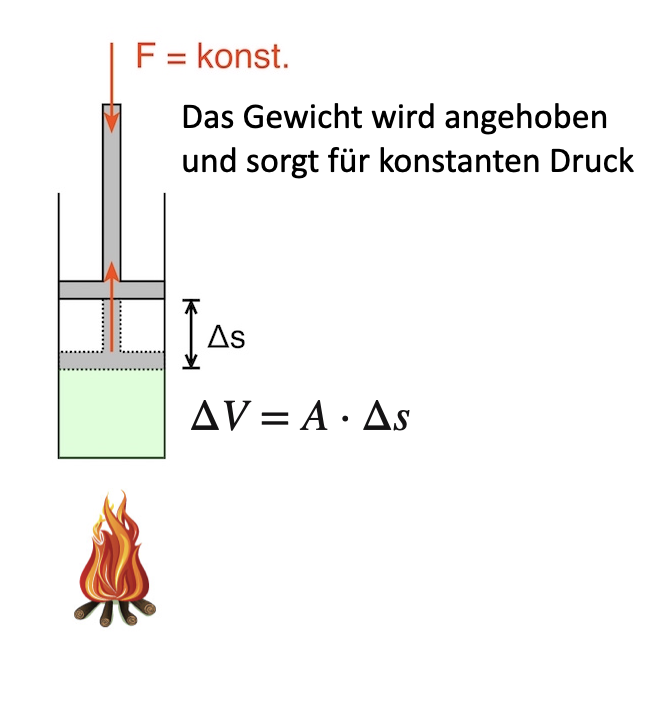
Fig. 9.9 Beispiel für eine isobare Zustandsänderung#
Wird der Stempel um \(\Delta s\) nach oben gedrückt, so beträgt die verrichtete Arbeit \(W = F \cdot \Delta s\) \(\rightarrow\) entspricht der Volumenänderungsarbeit!
\(p = \text{konst.} = \frac{F}{A} \Leftrightarrow F = p \cdot A \Rightarrow W = p \cdot \Delta V = p \cdot A \cdot \Delta s\)
9.3. Adiabate beziehungsweise isentrope Zustandsänderung#
Unter einer adiabaten Zustandsänderung (kurz: Adiabate) versteht man eine Zustandsänderung, bei der mit der Umgebung keine Wärme ausgetauscht wird. Es gilt als \(\Delta Q = 0\). Ist der Prozess zusätzlich noch reibungsfrei, sprich man von einem isentropen Prozess.
Dies wird im folgenden am Beispiel der adiabaten Kompression dargestellt.
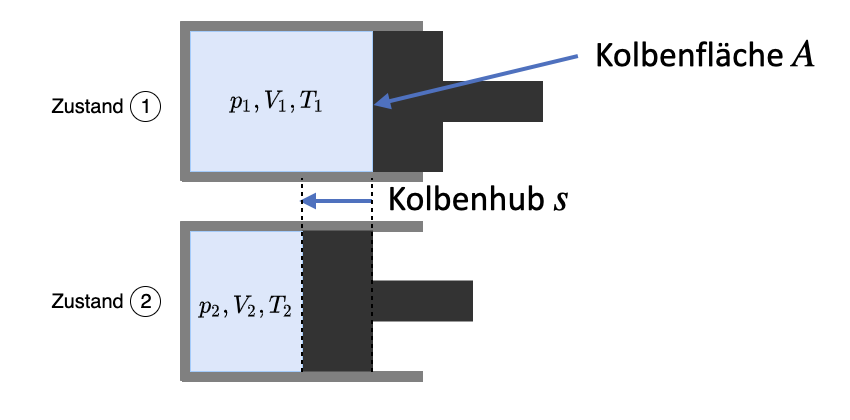
Fig. 9.10 Adiabate Kompression, wichtig ist eine sehr gute Isolation der Wände, damit \(\Delta Q = 0\) gilt.#
Für die innere Energie gilt
\(d U = dQ + dW \)
Da \(\Delta Q = 0\) folgt daraus
\(\rightarrow dU = dW\)
Das Volumen ändert sich, bei der Kompression wird am System Volumenänderungsarbeit verrichtet.
\(W = \int F \cdot ds = \int p\cdot A \cdot ds = - \int p\cdot dV\)
Mit Hilfe der idealen Gasgleichung ist
\(p \cdot V = n \cdot R \cdot T \Leftrightarrow p = \frac{n \cdot R \cdot T}{V}\)
\(\Rightarrow W = - \int \frac{n \cdot R \cdot T}{V}\cdot dV\)
somit ist
\(dW = -\frac{n \cdot R \cdot T}{V}\cdot dV\)
Gleichzeitig folgt aus der Definition der Wärmekapazität bei konstantem Volumen
\(dU=n \cdot c_{v}dT\)
Da \(dU = dW\) folgt daraus \(n \cdot c_{v}dT + \int \frac{n \cdot R \cdot T}{V}\cdot dV = 0\)
Diese Gleichung ist nur erfüllt, wenn
\(T \cdot V^{R/c_V} = \) konstant
Mit Hilfe der idealen Gasgleichung und \(\kappa = \frac{c_P}{c_V}\) und \(c_p = c_V +R\) lässt sich dies umformulieren zur Possoin’schen Adiabatengleichung
\(p\cdot V^\kappa = \) konstant
Damit sieht die Adiabate im \(p-V\)-Diagramm wie folgt aus:
Fig. 9.11 Adiabate Kompression im \(p-V\)-Diagramm.#
Für die Entropie gilt
Es wird keine Wärme mit der Umgebung ausgetauscht \(\Rightarrow \Delta Q = 0\)
Damit ist die Änderung der Entropie
\(\Rightarrow dS = \frac{d W_{diss}}{T}\)
Tritt keine Reibung auf, ist \(W_{diss}=0\) und somit auch \(dS = 0\). Daher nennt man die Adiabaten ohne Reibung auch Isentropen, nämlich Zustandsänderungen mit konstanter Entropie. Isentropen sind damit reversible Prozesse.
Das \(T-S\)-Diagramm ist daher sehr einfach
Fig. 9.12 Adiabate Kompression im \(T-S\)-Diagramm.#
Näherungsweise adiabatisch ablaufende Zustandsänderungen sind zum Beispiel
Zustandsänderungen in einem gut isolierenden Behälter Zustandsänderungen
so schnelle Zustandsänderungen, dass in der kurzen Zeit wenig Wärme zu- oder abfließen kann (schnell betriebene Luftpumpe)
Zustandsänderungen mit sehr großem Volumen, so dass Wärmeströme an seinem Rand praktisch keine Rolle spielen
9.3.1. Beispiel: (schnelle) Luftpumpe#
In einer Luftpumpe wird \(1 \, kg\) Luft (\(0^\circ C\) und \(1 \, bar\)) auf den 10-fachen Druck isentrop verdichtet. Wie hoch ist die Temperatur der verdichteten Luft?
Wie groß ist die Volumenändernderungsarbeit?
\(R_{Luft} = 287 \frac{J}{kg \cdot K}\) und \(\kappa_{Luft} = 1.4\)
Da es sich um eine adiabate Zustandsänderung handelt, gilt
\(p \cdot V^\kappa = \) konst
Darüber hinaus folgt aus der allgemeinen Gasgleichung
\(p \cdot V = m \cdot R_{Luft} \cdot T \Leftrightarrow V = \frac{m \cdot R_{Luft} \cdot T}{p}\)
Damit ergibt sich
\(p \cdot \left( \frac{m \cdot R_{Luft} \cdot T}{p} \right)^\kappa = \left( m \cdot R_{Luft} \cdot T\right)^\kappa \cdot p^\left( 1 - \kappa \right)\) = konst
Also ist mit
\(p_1 = 1 \, bar\) \(p_2 = 10 \cdot p_1 = 10 \, bar\) $T_1 = 0^\circ C = 273.15 , K
\(\left( m \cdot R_{Luft} \cdot T_1\right)^\kappa \cdot p_1^\left( 1 - \kappa \right) = \left( m \cdot R_{Luft} \cdot T_2\right)^\kappa \cdot p_2^\left( 1 - \kappa \right)\) \(\Leftrightarrow \left(T_1\right)^\kappa \cdot p_1^\left( 1 - \kappa \right) = \left(T_2\right)^\kappa \cdot p_2^\left( 1 - \kappa \right)\)
Damit ist
\(T_2 = 254 ^\circ C\)
Die Volumenänderungsarbeit ergibt sich wie folgt:
Aus der Definition von \(C_V\) ergibt sich
\(C_V = \left(\frac{dU}{dT} \right)_{V = \text{konst.}} \Leftrightarrow dU = C_V \cdot dT = m \cdot c_V \cdot dT \)
Damit gilt allgemein für ein ideales Gas für die Änderung der inneren Energie \(\Delta U\) durch Temperaturänderung \(\Delta T\)
\(\Delta U = m \cdot c_V \cdot \Delta T \)
Da bei Isentropen \(\Delta W = \Delta U \) gilt, ist die Volumenänderungsarbeit
\(\Delta W = \Delta U = m c_V \left( T_2 - T_1 \right)\)
In der Aufgabe sind \(R_S\) und \(\kappa\) gegeben.
Mit \(c_p = c_V +R_S\)
und \(\kappa = \frac{c_p}{c_V}\)
ergibt sich
\(\frac{c_V + R_S}{c_V} = \kappa \Leftrightarrow c_V + R_S = \kappa c_V \Leftrightarrow c_V = \frac{R_S}{\kappa -1}\)
und \(c_p = \kappa c_V = R_S \frac{\kappa}{\kappa-1}\)
Damit ist die Volumenänderungsarbeit
\(\Delta W = m c_V \left( T_2 - T_1 \right) = m \frac{R_S}{\kappa -1} \left( T_2 - T_1 \right) = 182.4 \, kJ\)
9.4. Isotherme Zustandsänderung#
Unter einer isothermen Zustandsänderung (kurz: Isotherme) versteht man eine Zustandsänderung, bei der die Temperatur des Systems konstant ist.
Dies wird im folgenden am Beispiel der isothermen Kompression dargestellt.
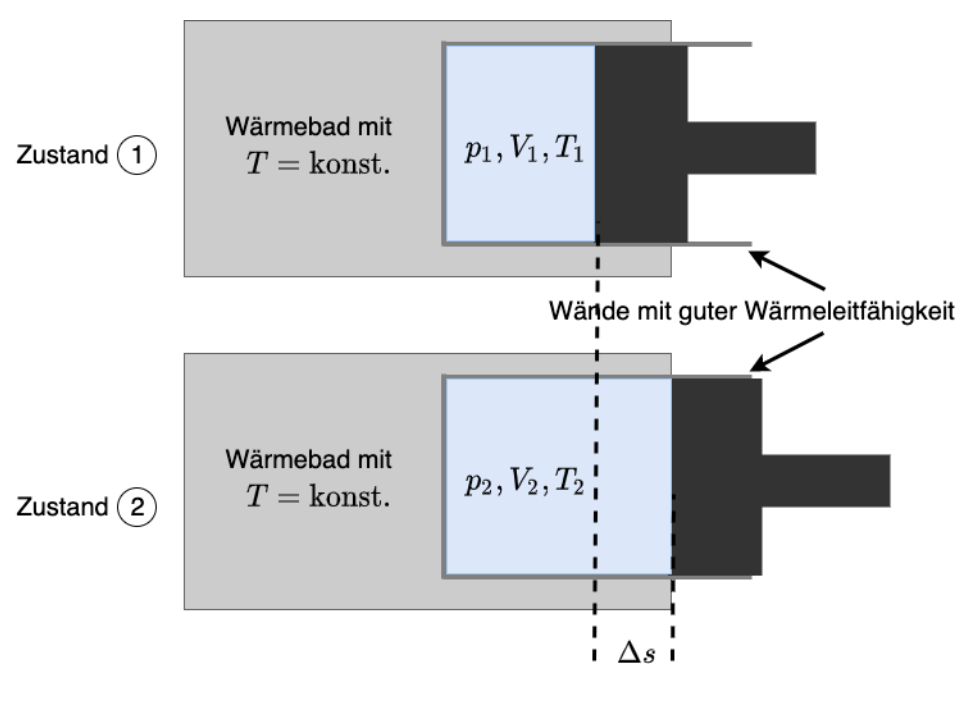
Fig. 9.13 Isotherme Kompression#
Da eine Kompression stattfindet, wird Volumenänderungsarbeit geleistet. \(W_{12} = - \int_1^2 p(V) \cdot dV = - \int_1^2 \frac{n R T}{V} \cdot dV = n R T \cdot ln \left( \frac{V_1}{V_2}\right)\)
Die gesamte bei einer Kompression zugeführte Arbeit muss quantitativ als Wärme an die Umgebung abgegeben werden, damit die Temperatur im System konstant bleibt.
Umgekehrt würde bei einer Expansion dieselbe Wärme aus der Umgebung aufgenommen werden.
Ist \(T = \) konstant folgt aus der idealen Gasgleichung
\(p \cdot V = n \cdot R \cdot T = \) konstant
Damit ist wie beim Gesetz von Boyle-Mariotte \(p \propto \frac{1}{V}\)
Das zugehörige \(p-V\)-Diagramm sieht daher wie folgt aus:
Fig. 9.14 \(p-V\)-Diagramm der isothermen Zustandsänderung#
Änderung der Entropie \(S\) ist für einen reibungsfreien Prozess: \(dS = \frac{d Q}{T} + \frac{dW_{diss}}{T} = \frac{d Q}{T}\)
Da \(T = \) konstanst ist, gilt
\(T \cdot dS = d Q \Rightarrow T \cdot \Delta S = \Delta Q \Leftrightarrow \Delta S = \frac{\Delta Q}{T}\)
Die hinzugefügte Wärme wirkt daher vollständig zur Erhöhung der Entropie.
Das \(T-S\)-Diagramm ist daher wieder einfach
Fig. 9.15 Isotherme Kompression im \(T-S\)-Diagramm.#
Die mit der \(S-\) Achse eingeschlossene Fläche ergibt die abgegebene Wärmemenge.
Fig. 9.16 Isotherme Kompression im \(T-S\)-Diagramm.#
9.4.1. sehr langsame Luftpumpe#
Näherungsweise realisierbar durch langsam verlaufende Zustandsänderungen, um den Temperaturausgleich mit der Umgebung zu ermöglichen (Bsp.: langsame Luftpumpe)
\(W_{12} = \int_1^2 p(V) \cdot dV = \int_1^2 \frac{n R T}{V} \cdot dV = n R T \cdot ln \left( \frac{V_2}{V_1}\right)\)
9.5. Polytrope Zustandsänderungen#
Isotherme und Isentrope bilden extreme Zustandsänderungen.
Bei der Isotherme ist \(\kappa = 1 \text{ und } p\cdot V^1 = \text{konst.}\)
Bei der Isentropen hingegen ist \(\kappa = \frac{c_p}{c_V} \text{ und } p\cdot V^{\frac{c_p}{c_V}} = \text{konst.}\)
Für ein ideales Gas ist \(\kappa = \frac{c_p}{c_V} = \frac{5}{3}\)
In der Realität kommen oft Zustandsänderungen vor, bei denen der Exponent zwischen \(1\) und \(\frac{5}{3}\) liegt. Man spricht dann von Polytropenexponenten \(n\) mit \(1 \le n \le \kappa\).
Beispielsweise ist für Luft \(n = 1.4 \rightarrow p \cdot V^{1.4} = \text{konst.}\)
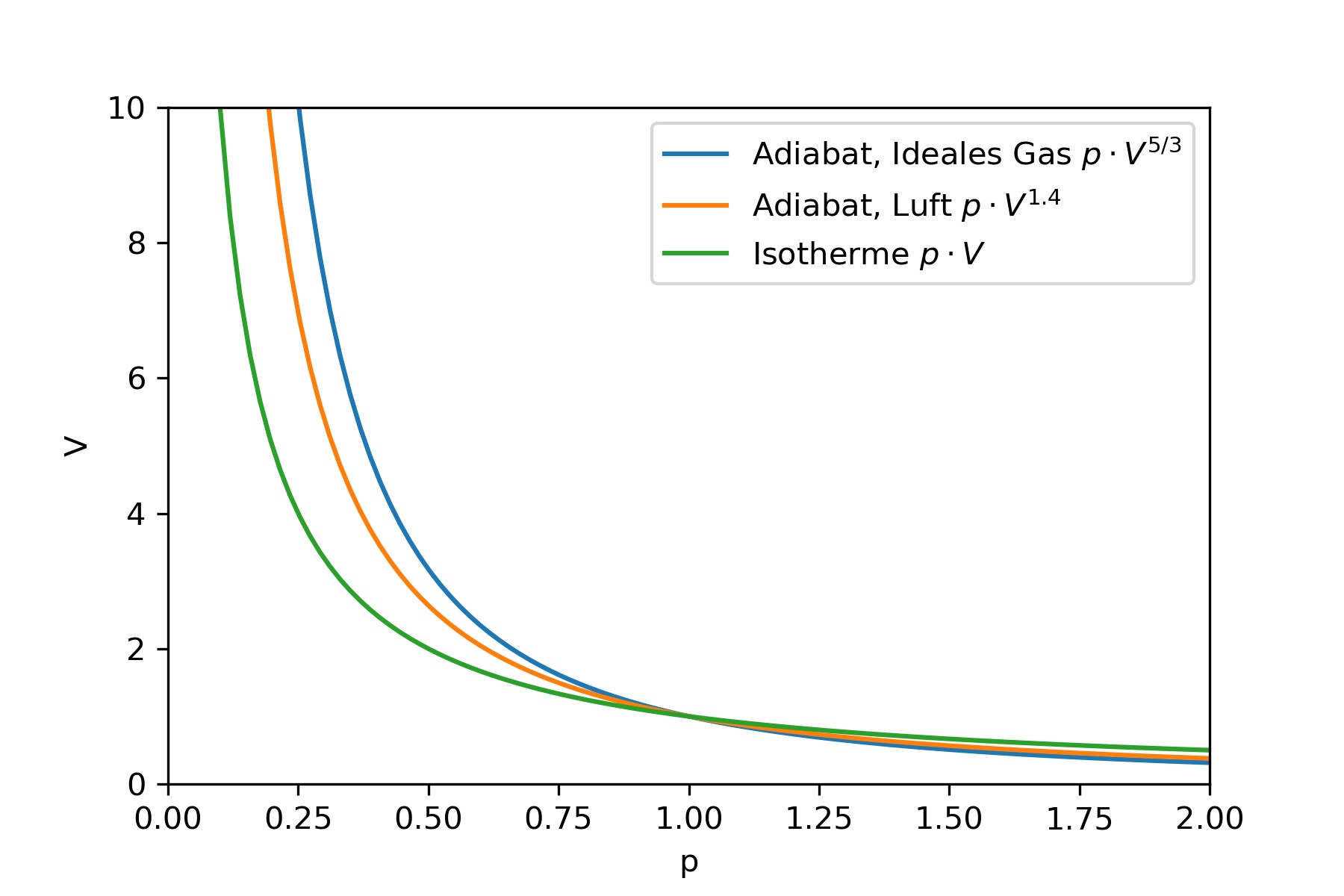
Fig. 9.17 Beispiel für eine polytrope Zustandsänderung anhand von Luft#
9.6. Umwandlungsenthalpie#
Bei einem Phasenübergang, beispielsweise vom flüssigen in den gasförmigen Zustand, wird Enthalpie aufgewand, um den Phasenübergang herbeizuführen. Die hinzugefügte Enthalpie führt dann beispielsweise nicht zur Erhöhung der Temperatur, sondern nur zur Umwandlung von einer Phase zur anderen. Diese Enthalpie bezeichnet man als Umwandlungsenthalpie.
