3.2. Differentialrechnung

Unter bestimmten Voraussetzungen kann eine Funktion differenziert werden. Das Differential einer Funktion beschreibt die Änderung der Funktion in jedem Punkt. Differenzierbarkeit ist die Eigenschaft einer Funktion, sich lokal um einen Punkt in eindeutiger Weise linear approximieren zu lassen. Differenzierbare Funktionen sind stets stetig. Das Differential oder die Ableitung einer Funktion ist definiert als

\(f^\prime(x) = lim_{h\rightarrow 0} \frac{f \left( x + h \right) - f \left( x \right)}{h} \)

Beispiel:

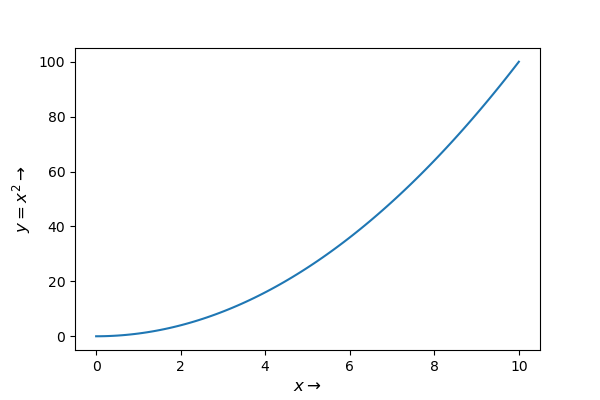
\(f(x) = x^2\)

\(f^\prime(x) = 2 \cdot x\)

Beispiel einer Funktion	Ableitung dieser Funktion

Es gibt eine Vielzahl von Rechenregeln für die Bildung von Ableitungen von Funktionen.

Die wichtigsten sind hier zusammengefasst.

Eine alternative Schreibweise zur Ableitung ist

\(f^\prime(x) = \frac{df}{dx}\).

In der Physik wird oft nach der Variablen Zeit abgeleitet. In dem Fall wird dies abkürzend dadurch kenntlich gemacht, dass ein \(\dot{}\) statt einem \(^\prime\) verwendet wird.

\(\frac{df}{dt} = \dot{f}\).