6. Stossprozesse

Stossprozesse bezeichnen Wechselwirkungsprozesse, bei denen zwei Massen mit unterschiedichen Geschwindigkeiten aufeinandertreffen und danach sich wieder voneinander wegbewegen. Dabei wird sowohl Energie als auch Impuls übertragen. Kennzeichnend für Stoßprozesse sind

• Kurze Wechselwirkungszeit, in der hohe Kräfte auftreten

• Abrupte Bewegungsänderung von mind. Einem der beteiligten Massen

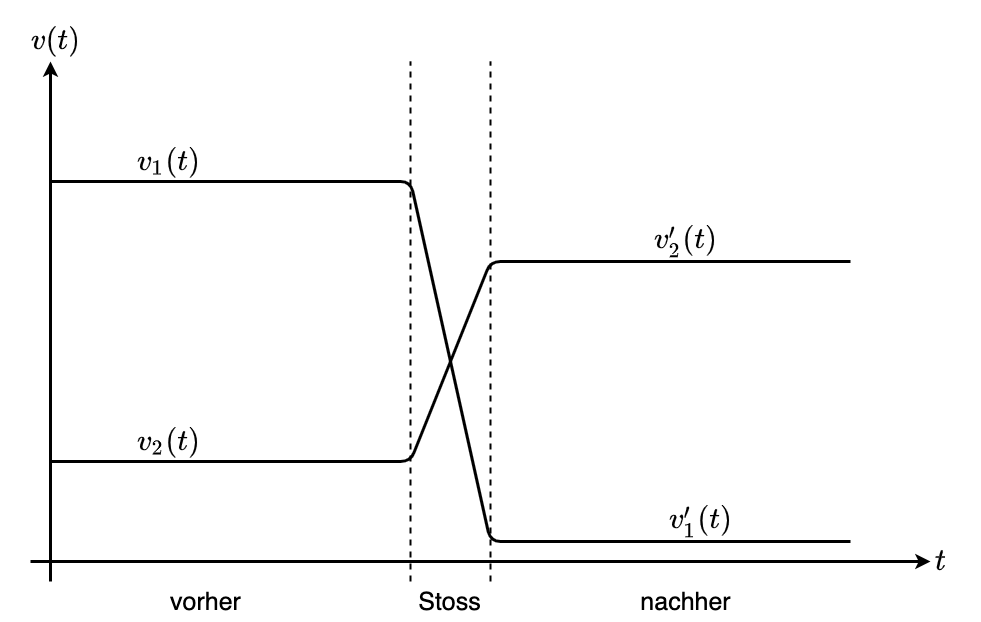
Fig. 6.1 Darstellung eines Stossprozesses.

Wichtige Größen für die Berechnung von Stoßprozessen

• Energieerhaltung \(E_{ges} = \text{konstant}\)

• Impulserhaltung \(\vec{p}_{ges} = \text{konstant}\)

Mit Hilfe dieser beiden Annahmen können Stossprozesse berechnet werden. Dazu werden die Situationen vor und nach dem Stoss betrachtet.

Fig. 6.2 Darstellung vor dem Stossprozess.

Vor dem Stossprozess bewegen sich beide Massen aufeinander zu. Um die Berechnungen möglichst einfach zu halten, wird ein Koordinatensystem gewählt, wir in Abbildung 6.2 dargestellt wird. So findet der Prozess in einer Ebene statt.

Fig. 6.3 Darstellung nach dem Stossprozess.

Nach dem Stoss bewegen sich die Massen dann mit verändertem Impuls und Energie voneinander weg.

Stossprozesse können durch verschiedene Eigenschaften klassifiziert werden. Die wichtigsten sind

Stossprozess	Eigenschaft
Glatter Stoss	Keine Reibungskräfte wirksam
	\(p_{1,\perp} = p_{2,\perp} = 0\)
Rauher Stoss	Im Berührungspunkt wirkende Reibungskraft
	Reibungskräfte müssen in der Energiebilanz berücksichtigt werden
	Impulsübertragung nicht \(\perp\) zur Berührungsebene
	\(p_{1,\perp} = - p_{2,\perp} \not= 0\)
Zentraler Stoß	Impulsübertragung entlang \(p_\parallel\) (entlang der Verbindungslinie der Schwerpunkte)
	Glatte Kugeln stoßen stets zentral
Dezentraler Stoß	Impulsübertragung nicht entlang \(p_\parallel\) (nicht entlang der Verbindungslinie der Schwerpunkte)
	Mindestens einer der beiden Stoßpartner wird in Rotation versetzt
Gerader Stoß	Beide Massen bewegen sich vor und nach dem Stoß entlang einer Geraden
	1-D Problem
Schiefer Stoß	Mindestens einer der beiden Stoßpartner hat vor dem Stoß eine Impulskomponente \(\perp\) zur Verbindungslinie der Schwerpunkte
Elastischer Stoß	Es tritt kein Verlust an kinetischer Energie auf
Unelastischer Stoß	Ein Teil der kinetischen Energie wird in andere Energieformen umgewandelt
	Reibung, Verformung, Änderung der inneren Energie