2.4. 2 dimensionale Bewegungen

Findet die Bewegung des Massenpunktes in zwei Dimensionen statt, wird die Ortskurve beschrieben durch den Vektor

\(\vec{r} = \left(\begin{array}{c} x \\ y\end{array}\right)\)

Bewegt sich der Massenpunkt frei, also gibt es keine Bedingungen für eine vorgegebene Bahn, hängen die Komponenten x und y jeweils nur von t ab.

\(\vec{r} = \left(\begin{array}{c} x (t) \\ y (t) \end{array}\right)\)

Komplizierter wird es, wenn es beispielsweise eine vorgegebene Bahn, wie beispielsweise bei einer Achterbahn, gibt. Dann hängen x und y voneinander ab und die Betrachtung der Bewegungsgleichung wird deutlich komplizierter.

Betrachtet wird im folgenden die freie Bewegung.

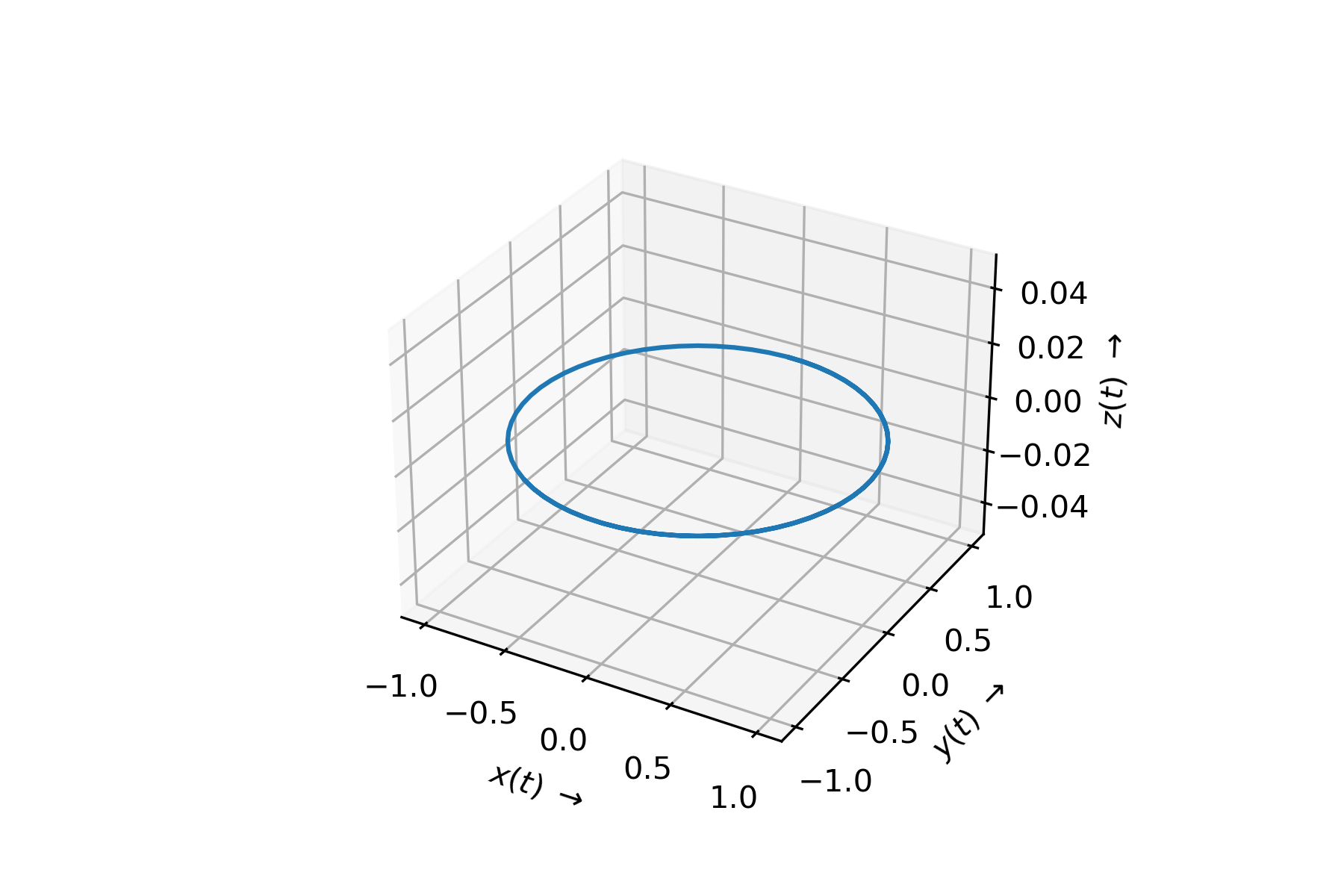
Fig. 2.11 Darstellung einer Bewegung in 2 Dimensionen.

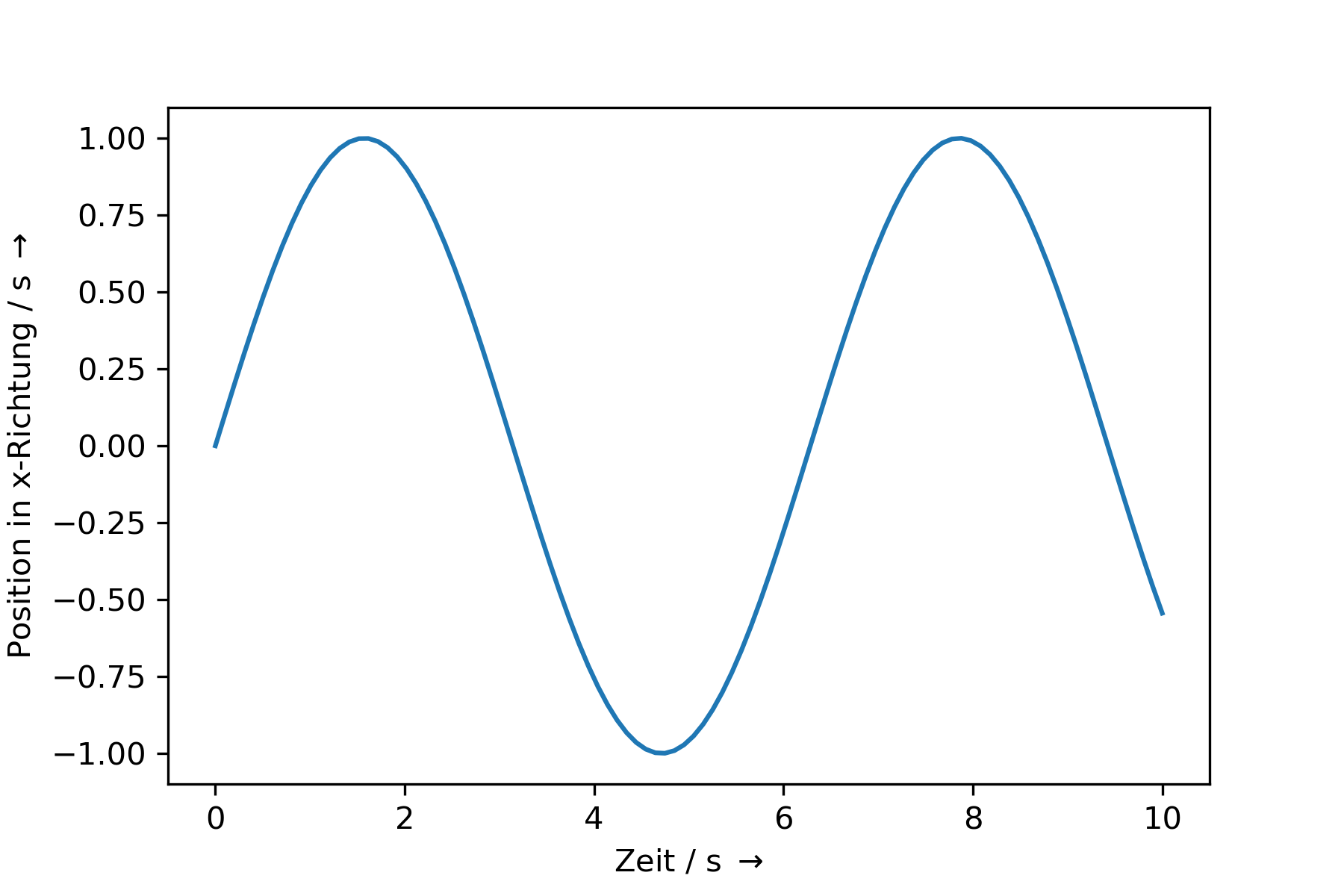
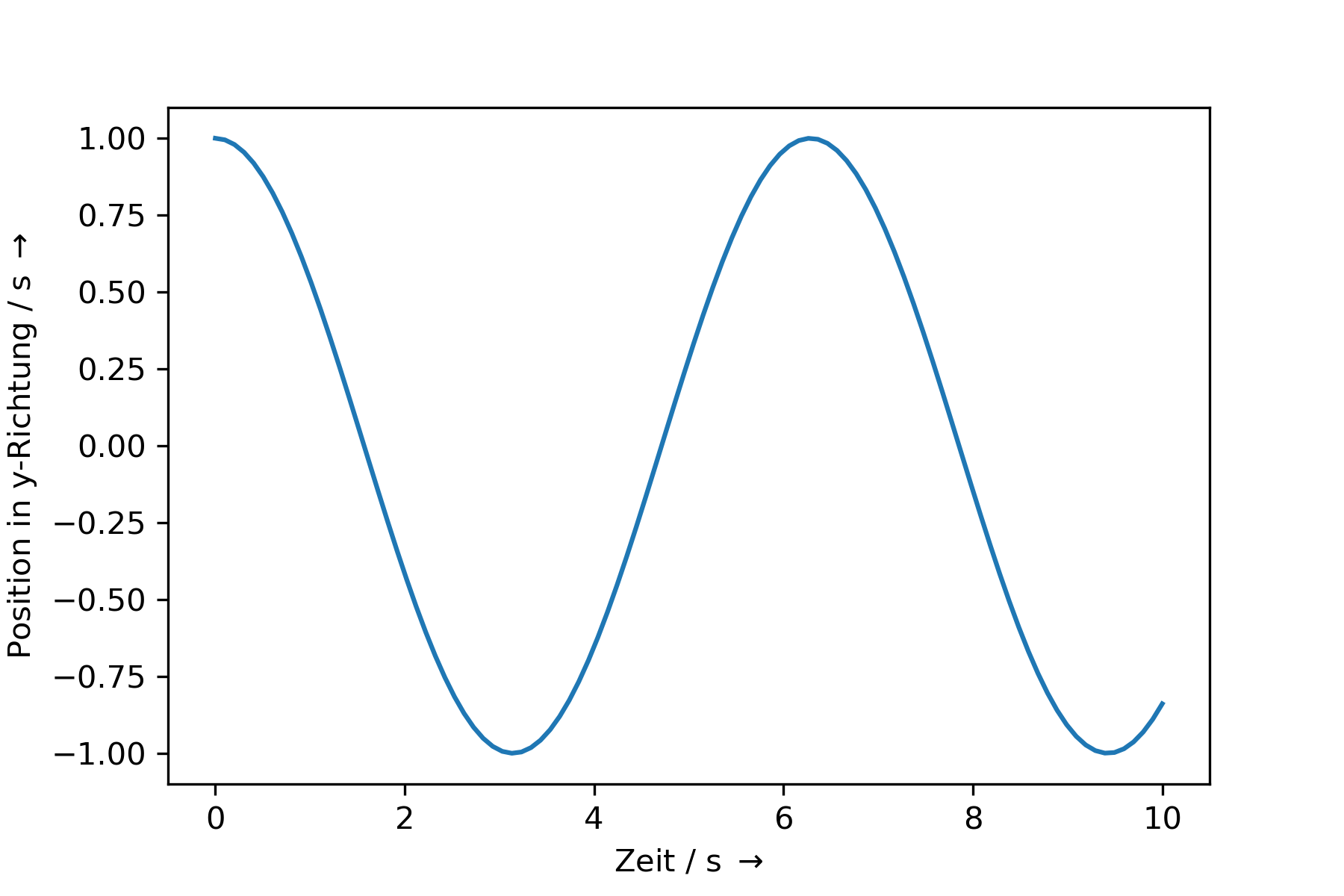
Diese lässt sich dann in folgenden zwei Ort-Zeit Diagrammen darstellen

x(t)	y(t)

Die Betrachtungen aus der eindimensionalen Bewegung können also auf jede Richtung einzeln übertragen werden. Ist die Beschleunigung in x-Richtung beispielsweise \(a_x(t) = t\) und in y-Richtung \(a_y(t) = \sqrt{t}\) so gilt (bei \(x_0 = y_0 = v_{x,0} = v_{y,0} = 0\))

\(a_x(t) = t\)

\(v_x(t) = \frac{1}{2} t^2\)

\(x(t) = \frac{1}{6} t^3\)

\(a_y(t) = \sqrt{t}\)

\(v_y(t) = \frac{2}{3} \sqrt{t^3}\)

\(y(t) = \frac{4}{15} \sqrt{t^5}\)

Daraus ergibt sich zusammengesetzt folgende Bewegung

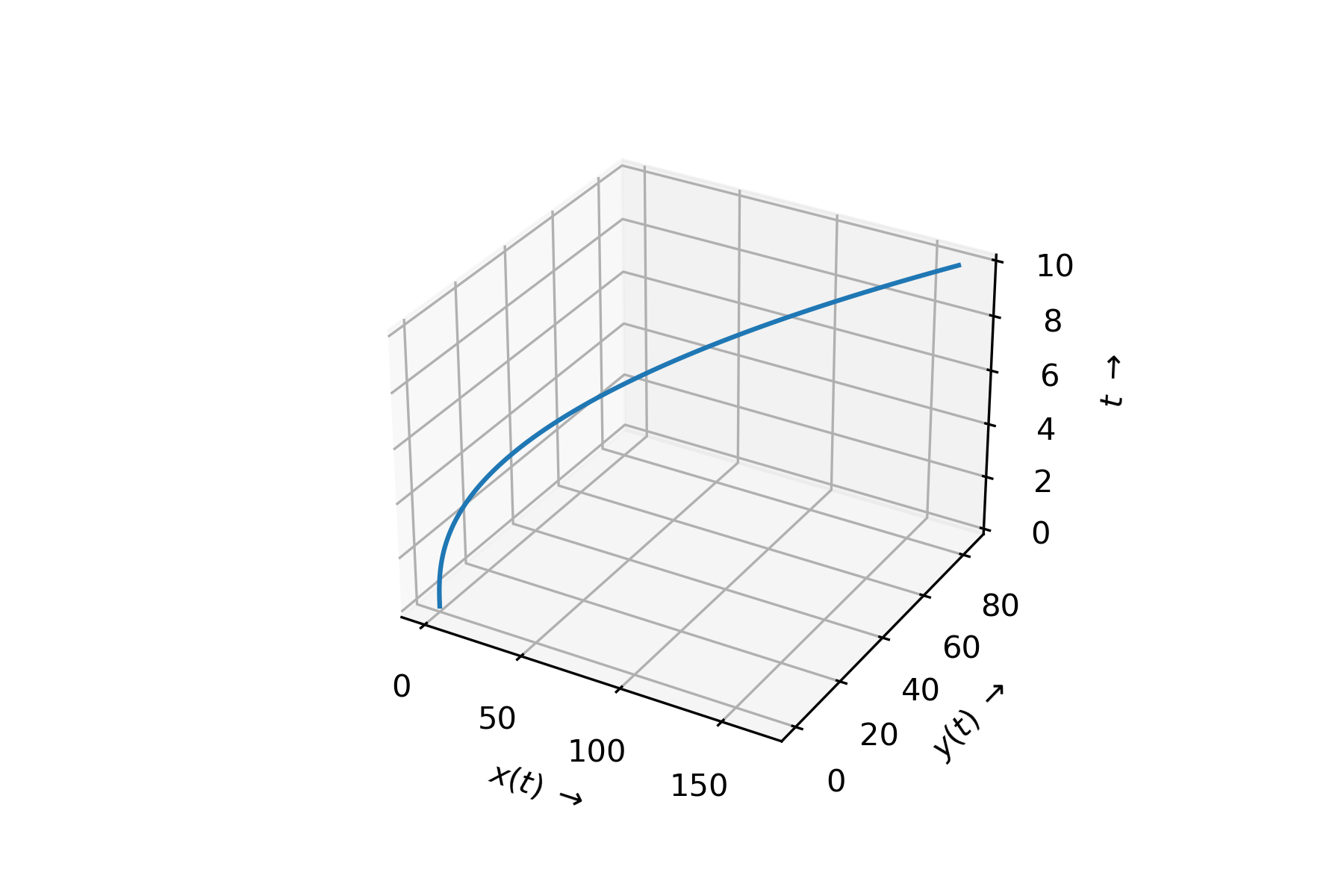
Fig. 2.12 Zusammengesetzte Bewegung.