4.1. Drehmoment und Drehimpuls#
Bei Drehbewegungen spielt nicht nur die Höhe der angreifenden eine Rolle, sondern auch der Abstand zur Drehachse. Die dazugehörende physikalische Größe ist das Drehmoment \(\vec{M}\). Das Drehmoment ist definiert als
\(\vec{M} = \vec{r} \times \vec{F}\)
Das Drehmoment ist also das Vektorprodukt aus Kraft und Hebelarm und steht senkrecht auf diesen beiden Größen.
Da das Drehmoment ein Vektorkreuzprodukt ist, gilt:
\(\left|\vec{M}\right| = \left|\vec{r}\right| \cdot \left|\vec{F}\right| \cdot sin \left( \angle (\vec{r},\vec{F}) \right)\)
Das Drehmoment ist demnach maximal, wenn \(\vec{r}\) und \(\vec{F}\) senkrecht aufeinander stehen. Sind \(\vec{r}\) und \(\vec{F}\) parallel ist das Drehmoment 0.
Entsprechend zu den Größen Kraft \(\vec{F}\) und Impuls \(\vec{p}\) gehört zum Drehmoment \(\vec{M}\) der Drehimpuls \(\vec{L}\) der definiert ist über
\(\vec{L} = \vec{r} \times \vec{p}\)
Der Drehimpuls ist eine Zustandsgröße, die beschreibt, wie sich eine Punktmasse auf einer kreisförmigen Bahnkurve bewegt.
Translation |
Rotation |
||
|---|---|---|---|
Kraft |
\(\vec{F} = \frac{d \vec{p}}{dt}\) |
Drehmoment |
\(\vec{M} = \frac{d \vec{L}}{dt}\) |
Impuls |
\(\vec{p}\) |
Drehimpuls |
\(\vec{L} = \vec{r} \times \vec{p}\) |
4.1.1. Gleichgewichtsbedingung#
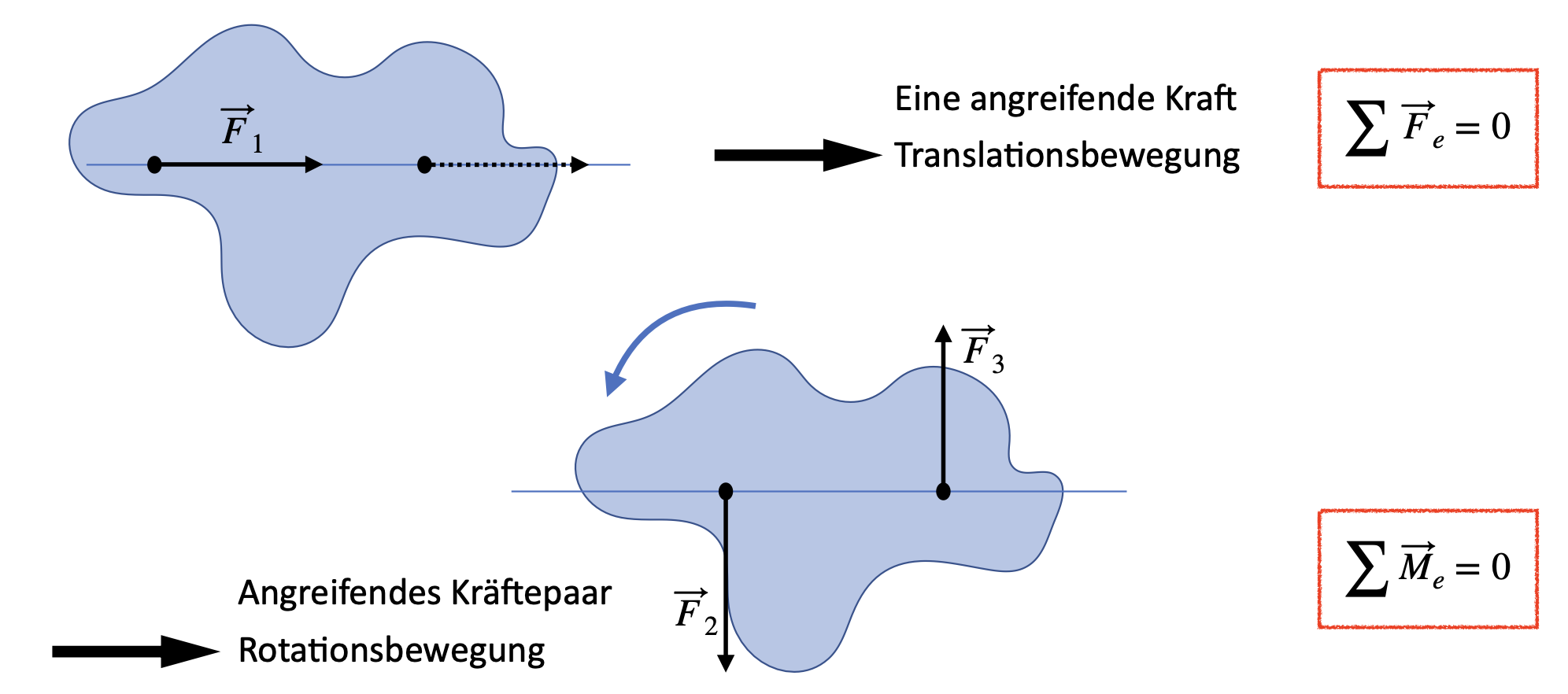
Fig. 4.4 Gleichgewichtsbedingung bei Rotation.#
Bei der Betrachtung von statischen Gleichgewichten gibt es, sofern Rotationsbewegungen möglich sind, zusätzlich die Bedinugung
\(\sum \vec{M} = \vec{0}\)
Dies bedeutet, dass im statiscchen Gleichgewicht die Summe der nach links drehenden Drehmomente und die Summe der nach rechts drehenden Drehmomente gleich ist.
\(\vec{M}_\circlearrowleft = \vec{M}_\circlearrowright\)
4.1.2. Beispiel: Kran#
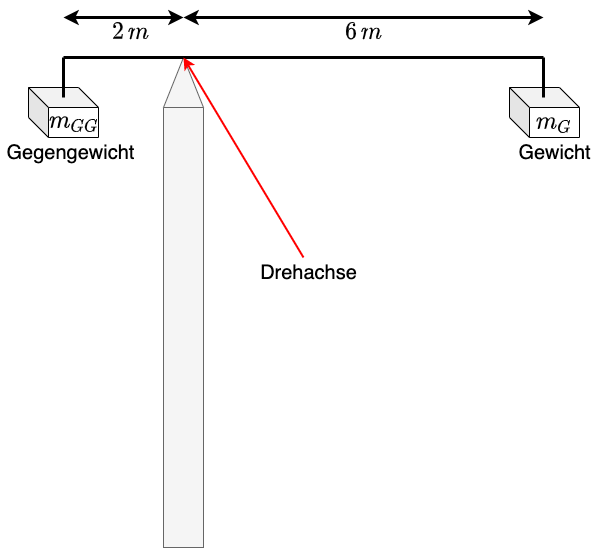
Fig. 4.5 Beispiel: Statisches Gleichgewicht mit Drehmoment.#
Der in Abbildung 4.5 dargestellte Kran trägt ein Gewicht mit \(m_G = 500 \, kg\). Wie schwer muss das Gegengewicht sein? Wenn statisches Gleichgewicht herrscht gilt
\(\sum \vec{M} = \vec{0} = \vec{M}_\circlearrowleft + \vec{M}_\circlearrowright\)
\(\Rightarrow \left| \vec{M}_\circlearrowleft \right| = \left| \vec{M}_\circlearrowright \right|\)
\(\left| \vec{M}_\circlearrowleft \right| = \left| \vec{r}_l \cdot m_{GG} \cdot \vec{g} \cdot sin \left( 90^\circ \right) \right| = r_l \cdot m_{GG} \cdot g\)
\(\left| \vec{M}_\circlearrowright \right| = \left| \vec{r}_r \cdot m_{G} \cdot \vec{g} \cdot sin \left( 90^\circ \right) \right|= r_r \cdot m_{G} \cdot g\)
\(\Rightarrow M_{GG} = \frac{r_r}{r_l} \cdot m_G = \frac{6 \,m}{2 \,m} \cdot 500 \, kg = 1500 \, kg\)
