1.1. Koordinatensysteme und Bezugssysteme

Physikalische Vorgänge finden immer in einem dazugehörigen Raum statt. Dies bedeutet, dass beispielsweise Bewegungen immer in Zusammenhang zu diesem definierten Raum stattfinden. Dieser Raum wird durch ein Koordinatensystem definiert.

Beispiel:

Eine zurückgelegte Entfernung soll angegeben werden. Dazu ist es notwendig zum einen den Startpunkt zu definieren, zum anderen die Einheit anzugeben, in der die Entfernung angegeben wird. Diese Angaben stellen bereits ein einfaches Koordinatensystem dar.

Ein Koordinatensytem mit räumlichen und einer zeitlichen Achse, welches dazu dient veränderliche physikalische Größen zu beschreiben, wird Bezugssystem genannt.

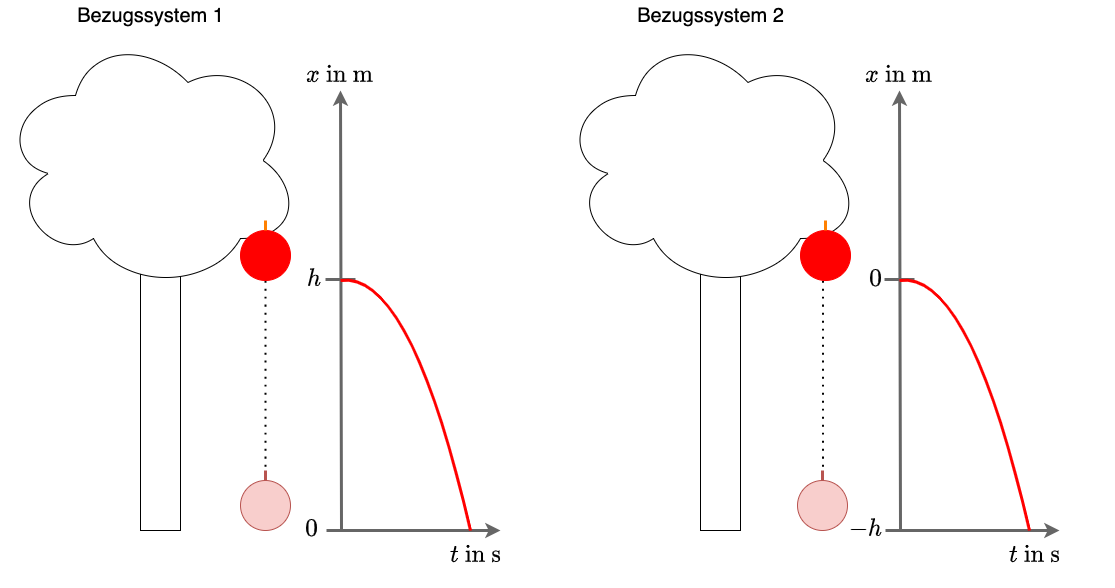
Fig. 1.2 Beispiele für Bezugssysteme

Die Abbildung 1.2 zeigt den Unterschied zwischen zwei Bezugssystemen. In beidem Fällen fällt ein Apfel vom Baum und die Höhe des Apfels wird abhängig von der vergangenen Zeit dargestellt. Im ersten Fall hat der fallende Apfel die Starthöhe \(h\). Am Ende des Falls is der Apfel bei einer Höhe \(0\) angekommen. Im zweiten Fall ist die Höhe zu Beginn \(=0\) und der Apfel hat bei Auftreffen auf den Boden die Höhe \(-h\). Möchte man also die Aussage treffen, auf welcher Höhe sich der Apfel befindet, muss immer das Bezugssystem mit angegeben werden, da die Information sonst nicht aussagekräftig ist.

Eines der bekanntesten Beispiele für ein Koordinatensystem ist das kartesische Koordinatensystem. Hier werden die Koordinatenachsen als gerade Linien jeweils senkrecht zueinander aufgetragen. In der Physik sind sogenannte rechtshändige Koordinatensysteme üblich (siehe Abbildung 1.3).

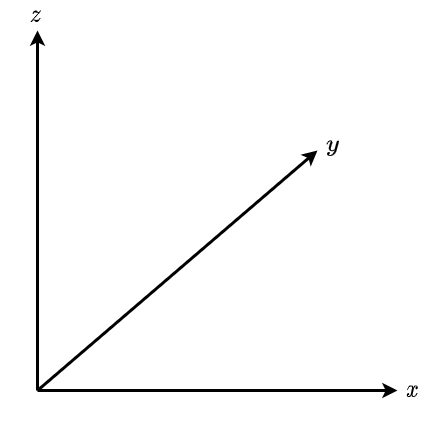
Fig. 1.3 Rechtshändiges kartesisches Koordinatensystem

In einem solchen Koordinatensystem können beispielsweise in drei Dimensionen drei räumliche oder zwei räumliche und eine zeitliche Komponente dargestellt werden.