8. Strömungen#
Eine (laminare) Strömung ist definiert als eine gerichtete Bewegung eines Fluids (siehe Abbildung 8.1). Es findet kein Massenaustausch der Schichten untereinander, da \(\perp\) zu Strömunggeschwingungkeit ein Impulsaustausch, aber kein Massenaustausch stattfindet.
Zunächst werden Effekte wie Reibung vernachlässigt. Reibung in Fluiden wird in Kapitel Grenzen des einfachen Modells beschrieben.
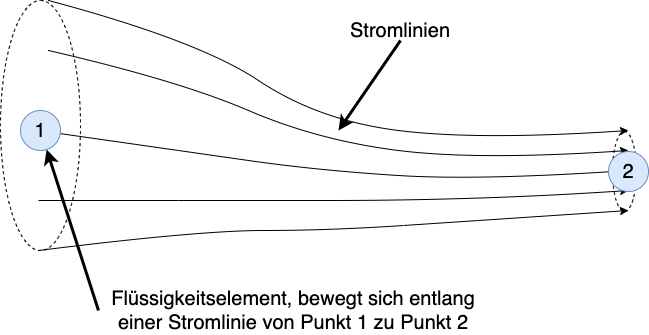
Fig. 8.1 Darstellung einer Strömung.#
Bei einer Strömung setzt sich der Gesamtdruck zusammen aus einem statischen und einem dynamischen Anteil. Der statische Druck wurde bereits im Kapitel Pascal’sches Gesetz hergeleitet. Für diesen gilt
\(p_{stat}(h) = \rho \cdot g \cdot h\)
Der dynamische Druck wird auch als Staudruck bezeichnet. Er resultiert aus der kinetischen Energie \(E_{kin}=\frac{1}{2} m v^2\) der strömenden Fluidelemente in einer Strömung. Der dynamische Druck ist definiert als
\(p_{dyn} = \frac{E_{kin}}{V}\)
Um eine laminare Strömung zu beschreiben, gibt es zwei wichtige Grundgleichungen, die in vielen Fällen helfen eine Strömung zu berechnen. Diese beiden Gleichungen sind die Kontinuitätsgleichung und der Satz von Bernoulli.
8.1. Kontinuitätsgleichung#
Betrachtet man einen Flüssigkeitstrom (beispielsweise durch eine Rohrleitung), so bleibt der Massenstrom (der bei inkompressiblen Medien gleich dem Volumenstrom ist) konstant. Denn die gleiche Menge Flüssigkeit, die in das Rohr hineinfließt, muss am Ende auch wieder hinausfließen, wenn keine Flüssigkeit verloren geht (siehe Abbildung 8.2).
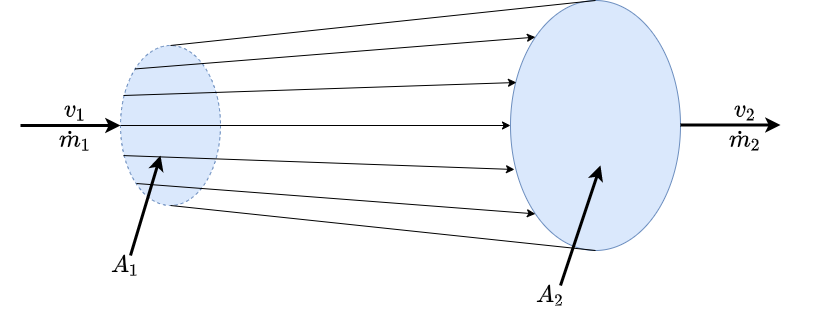
Fig. 8.2 Darstellung der Herleitung der Kontinuitaetsgleichung.#
Für den Massenstrom gilt:
\(\dot{m} = \dot{V} \cdot \rho = \frac{d}{dt} \left( V \right) \cdot \rho = \frac{d}{dt} \left( A \cdot x \right) \cdot \rho = A \cdot \frac{d}{dt} \left(x \right) \cdot \rho = A \cdot v \cdot \rho\)
Damit ergibt sich die Kontinuitätsgleichung, denn
\(A_1 \cdot v_1 \cdot \rho = A_2 \cdot v_2 \cdot \rho \Leftrightarrow A_1 \cdot v_1 = A_2 \cdot v_2 \Rightarrow A \cdot v = \text{konstant}\)
Kontinuitätsgleichung \(A \cdot v = \text{konstant}\)
8.2. Beispiel: Rohrstömung#
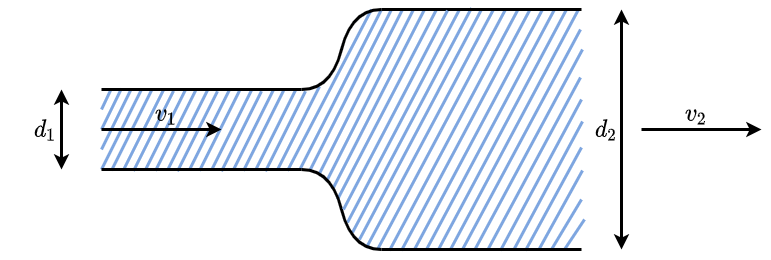
Fig. 8.3 Kontinuitaetsgleichung in einem Rohr#
Da eine Kreisförmige Grundfläche vorliegt, gilt
Fläche 1: \(A_1 = \left( \frac{d_1}{2}\right)^2 \cdot \pi \)
Fläche 2: \(A_2 = \left(\frac{d_2}{2} \right)^2 \cdot \pi\)
\(\Rightarrow A_1 \cdot v_1 = A_2 \cdot v_2 \Leftrightarrow \left( \frac{d_1}{2} \right)^2 v_1 = \left( \frac{d_2}{2} \right)^2 v_2 \Leftrightarrow v_2 = v_1 \left(\frac{d_1}{d_2}\right)^2\)
\(\Rightarrow\) Bei kleinerem Durchmesser ist die Geschwindigkeit höher!
8.3. Satz von Bernoulli#
Die Kontinuitätsgleichung betrachtet den Massenstrom in einer Strömung. Der Satz von Bernoulli ist gegeben durch die Energiebilanz einer (laminaren) Strömung und betrachtet den Gesamtdruck. Die Gesamtenergie setzt sich zusammen aus der Druckenergie, der potentiellen Energie und der kinetischen Energie
\(E = V\cdot p + m \cdot g \cdot h + \frac{1}{2} \cdot m \cdot v^2\)
Unter der Voraussetzung, dass es sich um ein abgeschlossenes System handelt, gilt Energieerhaltung. Die Gesamtenergie entlang einer Stromline ist somit konstant. Eine Stromline kann verstanden werden als der Weg, den ein Massenelement in einer laminaren Strömung zurückgelegt.
\(E = \text{konstant} \Rightarrow E_1 = E_2 \Leftrightarrow V\cdot p_1 + m \cdot g \cdot h_1 + \frac{1}{2} \cdot m \cdot v_1^2 = V\cdot p_2 + m \cdot g \cdot h_2 + \frac{1}{2} \cdot m \cdot v_2^2\)
Teilt man diese Gleichung durch das Volumen, ergibt sich der Satz von Bernoulli
\(p_1 + \frac{m}{V} \cdot g \cdot h_1 + \frac{1}{2} \cdot \frac{m}{V} \cdot v_1^2 = p_2 + \frac{m}{V} \cdot g \cdot h_2 + \frac{1}{2} \cdot \frac{m}{V} \cdot v_2^2\)
\(\Leftrightarrow p_1 + \rho \cdot g \cdot h_1 + \frac{1}{2} \cdot \rho \cdot v_1^2 = p_2 + \rho \cdot g \cdot h_2 + \frac{1}{2} \cdot \rho \cdot v_2^2\)
\(\Leftrightarrow p_{1,gesamt} = p_{2,gesamt}\)
Satz vor Bernoulli Entlang einer Stromlinie gilt \(p_{gesamt} = p_0 + \rho g h + \frac{\rho}{2}v^2\)
Dabei ist
\(p_0\) der Thermodynamische Druck, der derjenige Anteil des statischen Drucks ist, der nicht aus dem Eigengewicht des Fluids resultiert, sondern aus der inneren Energie des Fluids.
\(\rho g h\) der hydrostatische Druck
\(\frac{\rho}{2}v^2\) der dynamische Druck
Der Satz von Bernoulli gilt nur
entlang einer Stromlinie
für reibungsfreie Medien
Für wirbelfreie Strömungen
für inkompressible Strömungen, d.h Strömungen mit konstanter Dichte
8.3.1. Inkompressible Strömungen#
Inkompressible Strömungen sind definiert durch folgende Eigenschaften:
Strömungen, bei denen die Dichte nicht vom Druck abhängt, werden als inkompressibel bezeichnet
Vollständige Inkompressibilität ist ein theoretisches Konstrukt, auch Flüssigkeiten haben eine geringe Kompressibilität. Diese kann aber vernachlässigt werden, wenn sie hinreichend klein ist.
Gase sind kompressibel. In der Praxis kann eine Gasströmung unter bestimmten Umständen jedoch als inkompressibel angesehen werden. Die Dichte eines Gases hängt ab von der Temperatur T und von Druckänderungen \(\Delta p\). Da die Abhängigkeit von der Temperatur in der Praxis meist erheblich kleiner ist als Dichteänderungen auf Grund von Druckänderungen, wird ein Fluid als inkompressibel angesehen, wenn die Dichte entlang jeder Trajektorie konstant ist. Strömungen von prinzipiell kompressiblen Fluiden (z. B. von Gasen) können als inkompressibel angesehen werden, wenn die Mach-Zahl klein ist, also \(v \ll c\).
8.3.2. Beispiel: Laminare Rohrströmung#
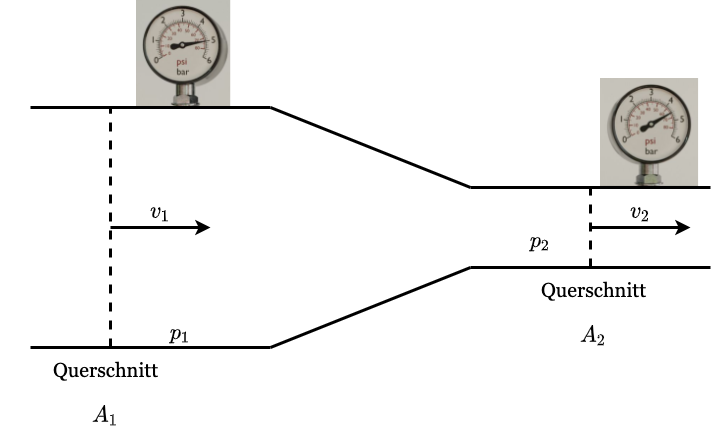
Fig. 8.4 Laminare Rohrströmung#
Entlang der Stromlinie gilt: \(h_1= h_2 = h\)
Bekannt sind \(v_1 = 4 \, m/s\) und \(p_1 = 4 \, bar\) (Überdruck) und der Rohrquerschnitt \(A_1 = 80 \, cm^2\)
Gesucht werden die Geschwindigkeit \(v_2\) und der Druck \(p_2\) im kleinen Rohr mit \(A_2 = 40 \, cm^2\)
Nach Bernoulli gilt:
\(p_1 + \frac{1}{2} \rho v_1 ^2 + \rho g h = p_2 + \frac{1}{2} \rho v_2 ^2 + \rho g h \Leftrightarrow p_1 + \frac{1}{2} \rho v_1^2 = p_2 + \frac{1}{2} \rho v_2^2\)
Aus der Kontinuitätsbedingung erhält man \(\Delta V = \text{konst.} = A_1 \, \Delta s_1 = A_2 \Delta s_2\)
Mit \(\Delta s = v \, \Delta t\) erhält man \(A_1 \cdot v_1 \cdot \Delta t = A_2 \cdot v_2 \cdot \Delta t \Leftrightarrow v_2 = v_1 \frac{A_1}{A_2} = \frac{8}{4}\cdot 4 \, m/s = 8 \, m/s \)
\(p_2 = p_1 + \frac{\rho}{2}\left(v_1^2 - v_2^2\right) = p_1 + \frac{\rho}{2} v_1^2\left(1 - \left( \frac{A_1}{A_2} \right)^2\right)\)
\(= 4 \cdot 10^5 \frac{N}{m^2} + \frac{1000 \, kg/m^3}{2}\cdot 4 \, m/s \cdot \left(1 - \left(\frac{80 \, cm^2}{40 \, cm^2}\right)^2 \right) \)
\(= 4 \cdot 10^5 \frac{kg}{m \cdot s^2} + \frac{1000 \, kg/m^3}{2}\cdot 4 \, m/s \cdot \left(1 - 4 \right) = 3.94 \, bar\)
8.3.3. Beispiel: Torricelli#
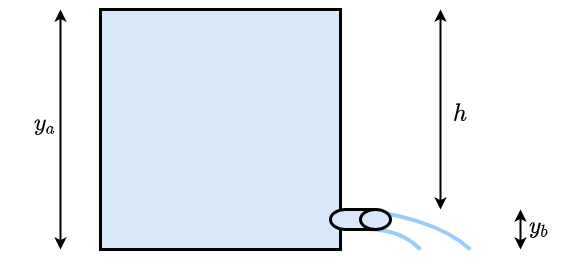
Fig. 8.5 Strömung aus einem großen Behälter#
Da das Loch im Tank wesentlich kleiner ist, als die Oberfläche des Tanks kann die Geschwindigkeit der Oberfläche vernachlässigt werden \(\rightarrow v_a \approx 0\)
Damit wird die Bernoulli-Gleichung zu \(p_a + \rho g y_a = p_b + \frac{1}{2} \rho v_b^2 + \rho g y_b\)
Da der Tank nach oben hin geöffnet ist und auch das Austrittsrohr mit der umgebenden Atmosphäre verbunden ist, sind die Umgebungsdrücke \(p_a\) und \(p_b\) gleich:
\(\Rightarrow \rho g y_a = \frac{1}{2} \rho v_b^2 + \rho g y_b \Leftrightarrow v_b^2 = 2 g \left( y_a - y_b\right) \Rightarrow v_b = \sqrt{2 g h}\)
Die Austrittsgeschwindigkeit hängt nur von der Höhendifferenz ab (Gesetz von Torricelli).
8.3.4. Beispiel: Venturi-Effekt#
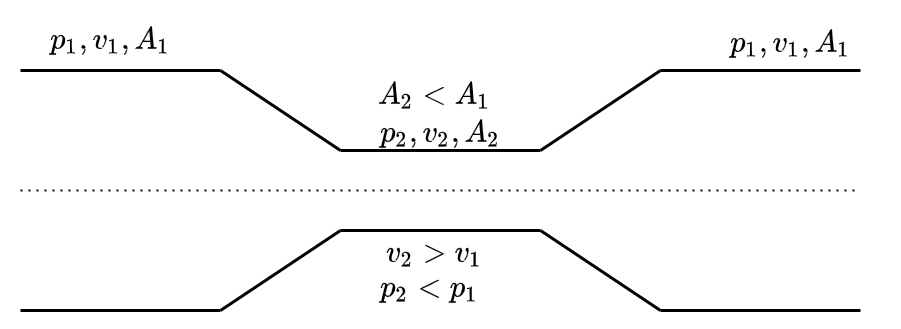
Fig. 8.6 Venturi-Effekt#
Entlang der Strömungslinie gilt \(h = \text{konst.} \Rightarrow p + \frac{1}{2} \rho v^2 = \text{konst.}\)
Kontinuitätsgleichung \(A \cdot v \cdot \Delta t = \text{konst.}\)
In obigem Abschnitt, wird gezeigt, dass wenn die Strömungsgeschwindigkeit einer inkompressiblen Strömung zunimmt, der Thermodynamische Druck fällt. Dies macht man sich beim Venturi-Effekt zunutze. Auf diese Art kann durch Messung des Differenzdrucks die Strömungsgeschwindigkeit in einer Rohrleitung gemessen werden.
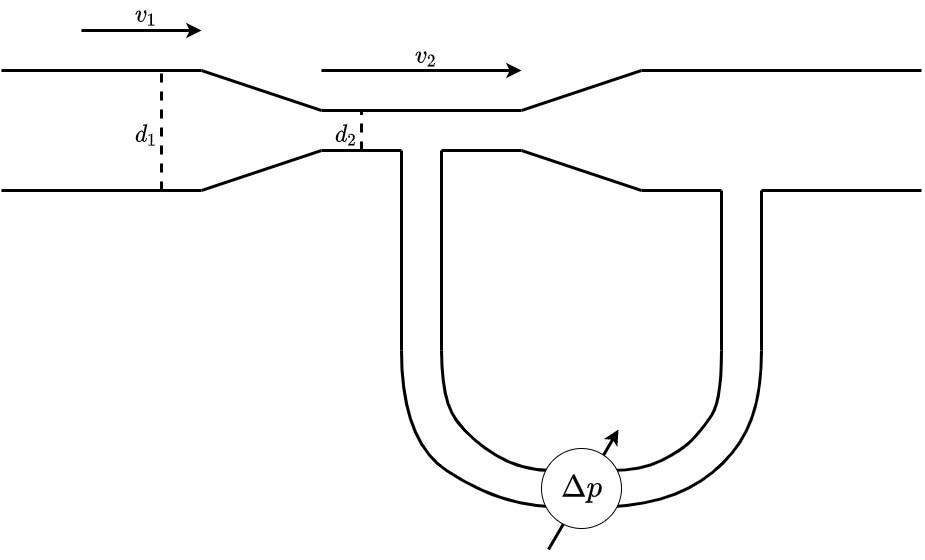
Fig. 8.7 Venturi-Effekt#
Aus der Kontinuitätsgleichung erhält man
\(A_1 v_1 = A_2 v_2 \Leftrightarrow \left( \frac{d_1}{2} \right)^2 \pi v_1 = \left( \frac{d_2}{2} \right)^2 \pi v_2 \Leftrightarrow v_2 = v_1 \frac{d_1^2}{d_2^2}\)
Aus dem Satz von Bernoulli erhält man
\(p_1 + \frac{1}{2} \cdot \rho \cdot v_1^2 = p_2 + \frac{1}{2} \cdot \rho \cdot v_2^2 \Leftrightarrow p_1 - p_2 = \Delta p = \frac{\rho}{2} \left( v_2^2 - v_1^2 \right) = \frac{\rho\cdot v_1^2}{2} \left( \left( \frac{d_1}{d_2} \right)^4 - 1 \right) \)
Damit ergibt sich für die Geschwindigkeit der Rohrströmung
\(\Rightarrow v_1^2 = \frac{2\cdot \Delta p}{\rho \left( \left( \frac{d_1}{d_2} \right)^4 - 1 \right)} \Leftrightarrow v_1 = \sqrt{\frac{2\cdot \Delta p}{\rho \left( \left( \frac{d_1}{d_2} \right)^4 - 1 \right)}}\)
Eine weitere Anwengung ist die Venturi Düse. Hierbei wird der entstehende niedrige Thermodynamische Druck genutzt, um eine Flüssigkeit aus einem Behälter anzusaugen und fein zerstäubt auszupusten (siehe Abbildung 8.8).
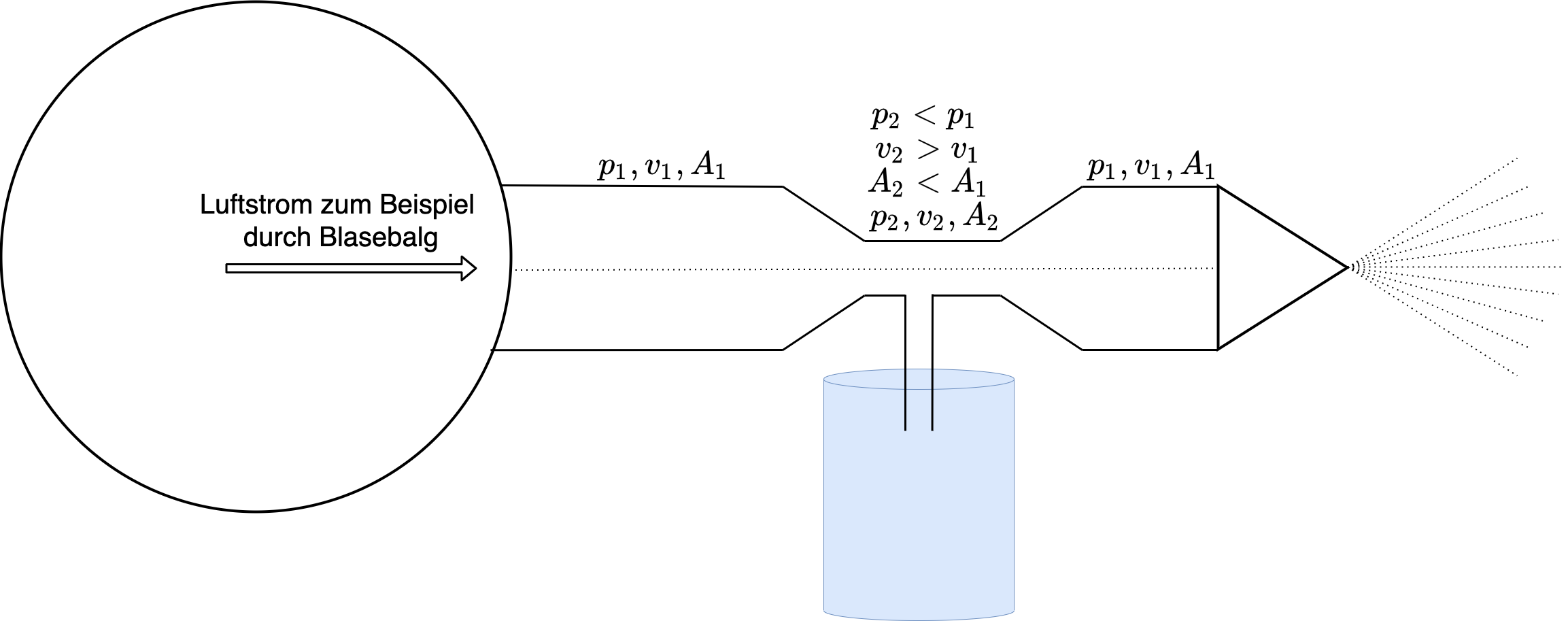
Fig. 8.8 Venturi-Düse#
