7. Diffusion

Als Diffusion wird der ohne äußere Einwirkung eintretende Ausgleich von Konzentrationsunterschieden in Stoffgemischen bezeichnet. Dieser Ausgleich entsteht durch statistisch verteilte Eigenbewegungen der Teilchen. Um Diffusion zu verstehen, werden nicht die Bewegungsgleichunten der einzelnen Teilchen betrachtet, sondern die Bewegungen werden statistisch betrachtet. Das Phänomen der Diffusion wird in diesem Skript nur qualitativ diskutiert.

Die Diffusion führt mit der Zeit zur vollständigen Durchmischung zweier oder mehrerer Stoffe durch die gleichmäßige Verteilung der beweglichen Teilchen und erhöht damit die Entropie des Systems.

Diffusion findet in mikroskopischen Skalen statt (bewirkt aber auf mikroskopische Skalen sichtbare Effekte)

Ursache für die Diffusion ist die statistische Bewegung der Teilchen, sie wird beschrieben durch die Brown’sche Molekularbewegung.

Die brownsche Molekularbewegung wurde 1827 von Robert Brown entdeckt und später von Einstein theoretisch hergeleitet Sie beschreibt die Masse und Temperaturabhängige zufällige Bewegung von mikroskopisch kleinen Teilchen; je geringer die Teilchenmasse, desto stärker ist bei einer bestimmten Temperatur ihre Bewegung. Sie kommt zustande durch Zusammenstöße der Teilchen, die beim Aufprallen Impulse auf die Teilchen übertragen und zur Verschiebung der Teilchen führen.

Der mittlere quadratische Abstand zwischen den Teilchen ist \(\bar{x}^2 = \frac{k_B \cdot T}{2 \cdot \pi \cdot \eta \cdot r} \cdot t\)

\(k_B = \) Boltzmannkonstante \(= 1.380649 \cdot 10^{-23} \frac{J}{K}\)

\(\eta = \) Viskosität der Flüssigkeit / des Gases

\(r = \) Teilchenradius

\(T = \) absolute Temperatur

Fig. 7.1 Brown’sche Molekularbewegung Von Jkrieger, Deutschen Krebsforschungszentrum, Arbeitsgruppe B040 Biophysik der Makromoleküle

Dies bedeutet im Einzelnen

• Je höher die Temperatur ist, desto schneller die Teilchenbewegung, damit ist auch die Durchmischen schneller.

• Teilchen in einem viskosem (dickflüssigem) Medium können nicht so schnell diffundieren wie in einem leichtflüssigem Medium.

• Je größer die Teilchen sind, desto größer ist der Widerstand, den das Medium diesen Teilchen leistet.

Der Verlauf der Durchmischung wird durch die Diffusionsgleichung beschrieben. Diese gilt für gelöste Stoffe in Flüssigkeiten und für Gase. Sie kann in eigeschränkter Form sogar auf Festkörper angewendet werden.

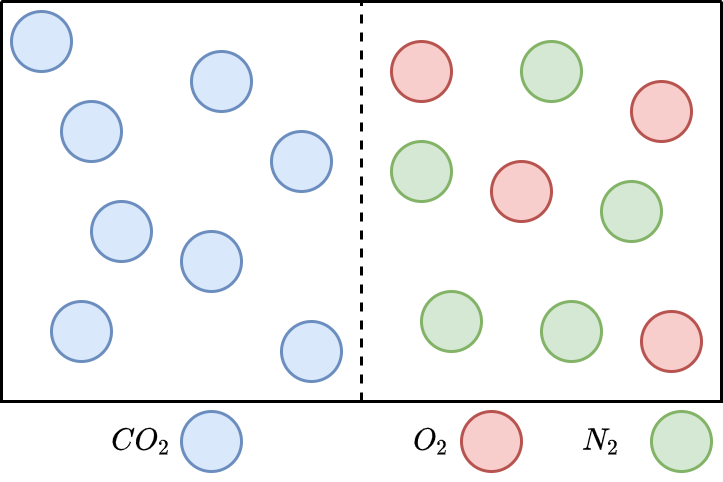
Fig. 7.2 Diffusion durch eine Fläche

Die Teilchendichte ist definiert \(c = \frac{N}{V}\).

Die Anzahl der Teilchen, die durch \(A\) hindurch diffundieren ist \(\frac{dN}{dt} = -D \cdot A \frac{dc}{dx}\), wobei \(D\) der Diffusionskoeffizient ist. Dieser hängt unter anderem ab von der Temperatur und vom Druck. Alternativ wird die Schreibweise \(J = -D \frac{dc}{dx}\) verwendet, wobei \(J = \frac{1}{A}\dot{N}\) die Teilchenstromdichte ist.

Der Diffusionskoeffizient unterscheidet sich je nach Aggregatzustand stark. In Flüssigkeiten und Gasen wird der Diffusionskoeffizient durch die Einstein-Stoekes Gleichung beschrieben \(D = \frac{k_B \cdot T}{6 \cdot \pi \cdot \eta \cdot R_0}\), in Gasen ist der Diffusionskoeffizient viel größer als in Flüssigkeiten. In Feststoffen zeigt sich ein ganz anderes Verhalten, die Teilchen müssen zwischen verschiedenen Gitterplätzen springen. . Dabei müssen die Teilchen eine Energiebarriere E überwinden, es gilt \(D = D_0 e^{-\frac{E}{RT}}\).