4.4. Zentrifugalkraft

Fig. 4.9 Zentrifugalkraft.

Die Zentrifugalkraft ist eine Trägheitskraft, die bei Dreh- und Kreisbewegungen auftritt und radial von der Rotationsachse nach außen gerichtet ist (siehe rotierendes Bezugssystem).

Oft wird auch von einer Zentrifugalkraft gesprochen, diese hängen wie folgt zusammen:

• Die Zentripetalkraft und Zentrifugalkraft wirken bei einer beschleunigten Kreisbewegung und haben betragsmäßig die gleiche Formel. Es handelt sich um entgegengesetzte Kräfte, die abhängig von dem Bezugssystem sind.

• Die Kraft, welche einen Körper auf eine Kreisbahn zwingt, wird Zentripetalkraft genannt. Sie ist stets senkrecht zum Geschwindigkeitsvektor und zum Kreismittelpunkt gerichtet (Zwangsbedingung).

• Die Zentrifugalkraft drückt den Körper im rotierenden Bezugssystem nach außen.

Zentripetalkraft

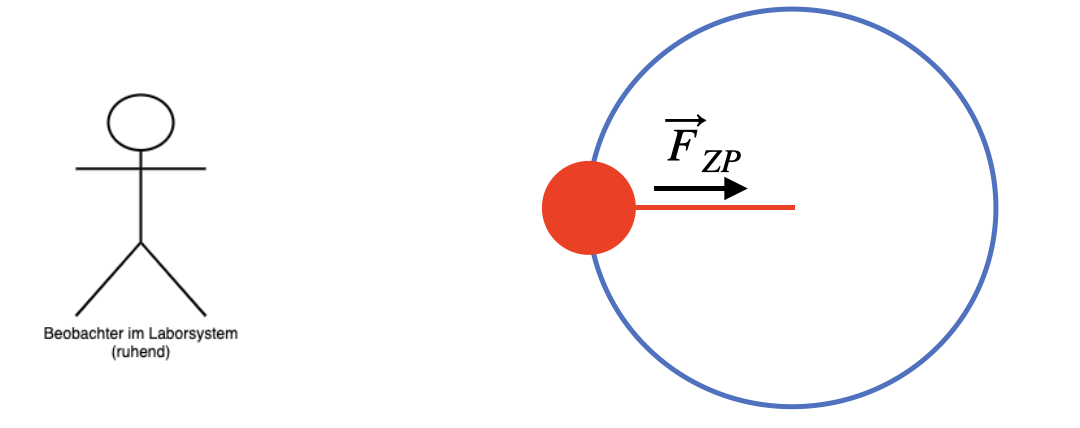
Fig. 4.10 Zentripetalkraft.

Wird die Kreisbewegung eines Körpers vom Laborsystem aus beschrieben (Beobachter im ruhenden Laborsystem) so wirkt die Zentripetalkraft auf den Körper. Wäre diese zum Mittelpunkt der Kreisbewegung gerichtete Kraft nicht vorhanden, so würde der Körper nach dem Trägheitssatz in Tangentenrichtung wegfliegen ist eine sogenannte „Zwangskraft“ und wird generiert durch eine Zwangsbedingung, z.B. ein Seil, welches den Körper auf der Kreisbahn hält.

Zentrifugalkraft

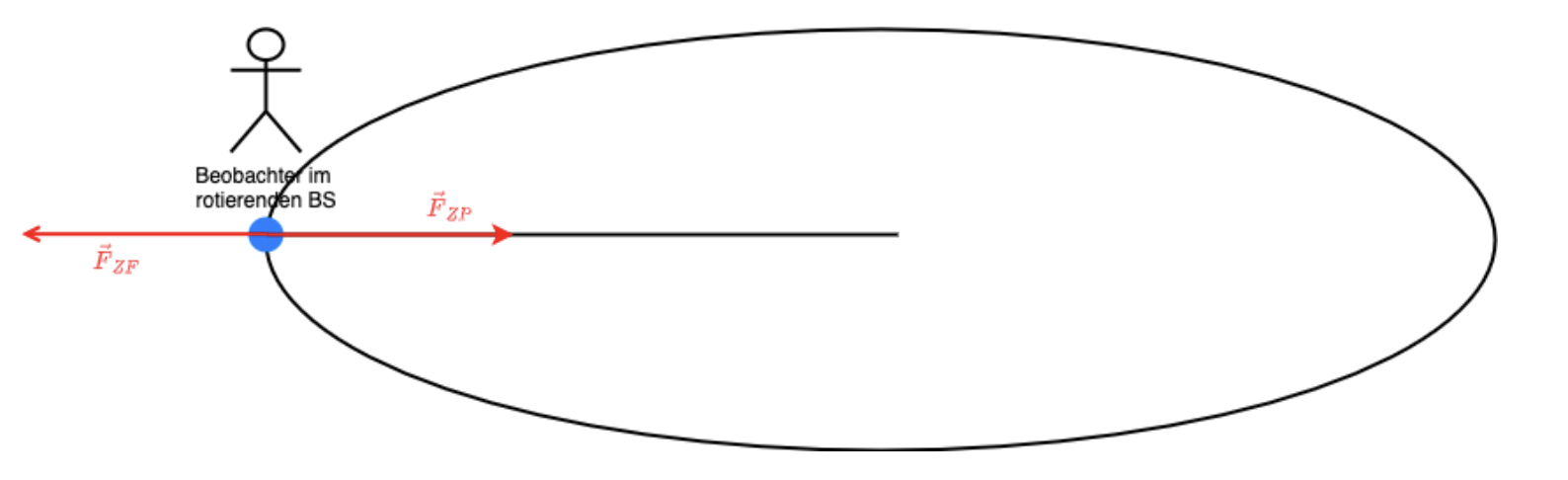
Fig. 4.11 Zentrifugalkraft.

Im bewegten Bezugsystem spürt der Beobachter die Zentrifugalkraft, die ihn nach außen drückt, aber auch gleichzeitig die Zentripetalkraft, die ihn auf der Kreisbahn hält.

4.4.1. Kreisbahn

Im Falle einer Kreisbahn, vereinfachen sich die Gleichungen. Allgemein gilt für die Zentrifugalkraft:

\(\vec{F}_Z = m \vec{\omega} \times \left( \vec{\omega} \times \vec{r}^\prime\right)\)

Da es ein Kreuzprodukt ist, gilt:

\(\left| \vec{\omega} \times \vec{r}^\prime\right|=\left|\vec{\omega} \right|\cdot \left|\vec{r}^\prime \right|\cdot sin \left(\angle \vec{\omega},\vec{r}^\prime\right)\)

Bei der Kreisbewegung stehen \(\vec{r}\) und \(\vec{\omega}\) senkrecht aufeinander.

\(\Rightarrow \left|\vec{F}_Z \right| = m \omega^2 r^\prime\), wenn \(\vec{\omega} \perp \vec{r}^\prime\)

4.4.2. Beispiel: Aufgabe: Wasser in einem Glas

Ein Wasserglas wird mit konstanter Umlaufgeschwindigkeit gedreht, dadurch wird Wasser nach außen gedrückt und es bildet sich eine gekrümmte Oberfläche. Wie sieht diese Oberfläche aus?

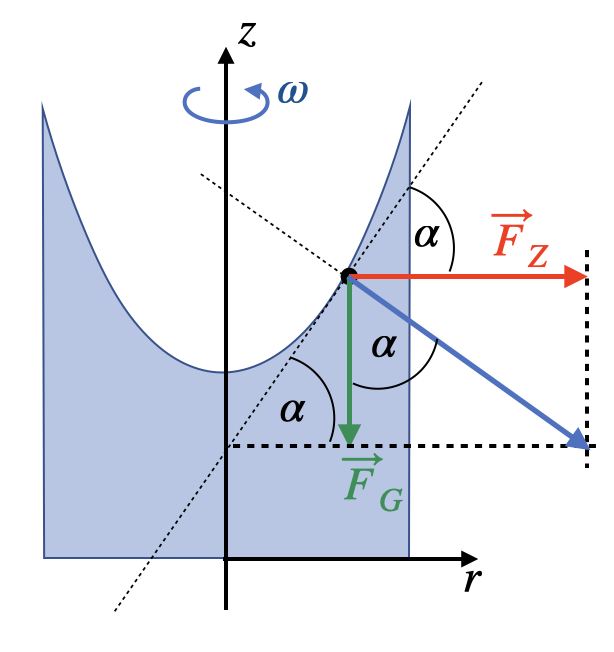
Fig. 4.12 Rotierendes Wasserglas.

Kräftebilanz: \(\vec{F}= \vec{F}_G + \vec{F}_Z\)

Darüber hinaus gilt für den Winkel \(\alpha\)

\(tan \left( \alpha \right)= \frac{\left| \vec{F}_Z \right|}{\left| \vec{F}_G \right|} = \frac{m \omega^2 r}{mg} = \frac{\omega^2 r}{g}\)

Der Winkel \(\alpha\) gibt außerdem die Steigung der Tangente der Funktion \(z(r)\) an.

\(tan \left( \alpha \right) = \frac{dz}{dr} \Rightarrow \frac{dz}{dr} = \frac{\omega^2 r}{g} \Leftrightarrow dz = \frac{\omega^2 r}{g} dr\)

\(\int_{z_0}^z dz = \int_0^r \frac{\omega^2 r}{g} dr \Leftrightarrow z - z_0 =\frac{\omega^2 r^2}{2g} \)

\(\Leftrightarrow z = \frac{\omega^2 r^2}{2g} + z_0\)

4.4.3. Beispiel: Karussell

Wie hoch fliegt das Gewicht bei Karussell?

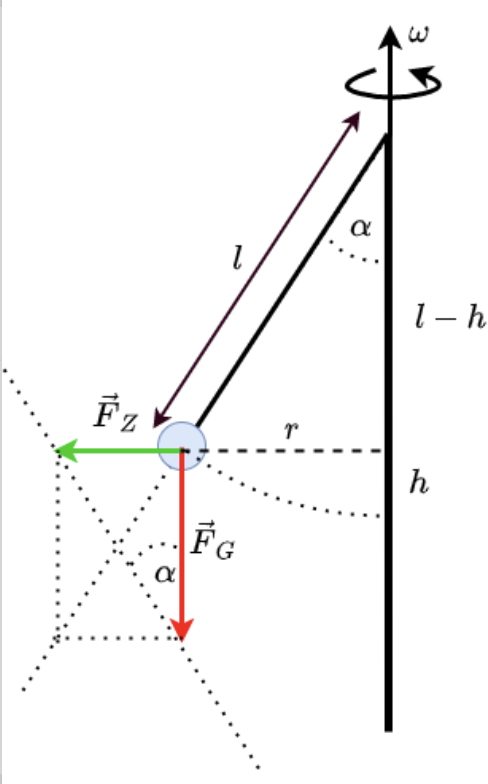
Fig. 4.13 Kettenkarusell.

Für den Winkel \(tan \left(\alpha \right)\)

\(tan \left( \alpha \right) = \frac{\left| \vec{F}_Z\right|}{\left| \vec{F}_G\right|} = \frac{\omega^2 r}{g}\)

Darüber hinaus gilt \(sin \left(\alpha\right) = \frac{r}{l} \Leftrightarrow r = l \cdot sin \left(\alpha\right) \Rightarrow tan \left(\alpha \right) = \frac{l\cdot sin(\alpha) \cdot \omega^2}{g}\)

mit \(tan (\alpha) = \frac{sin(\alpha)}{cos(\alpha)} \Leftrightarrow \frac{tan(\alpha)}{sin(\alpha)} = cos^{-1} (\alpha)\)

\(\Rightarrow cos^{-1}(\alpha) = \frac{l \omega^2}{g} \Leftrightarrow cos(\alpha) = \frac{g}{l \omega^2}\)

und es gilt

\(cos(\alpha) = \frac{l-h}{l}\)

\(\Rightarrow \frac{g}{l\omega^2} = \frac{l-h}{l} \Leftrightarrow h = l-\frac{g}{\omega^2}\)

4.4.4. Beispiel: Bobbahn

Fig. 4.14 Bobbahn in St.Moritz, (Von Sandro Halank)

Wie groß ist der Radius der Horse-Shoe-Kurve der Bobbahn von St. Moritz Celerina, wenn die Betreiber angeben, dass dort bei der erreichten Geschwindigkeit von \(v = 145 \, \frac{km}{h}\) auf den Fahrer eine Kraft wirkt, die fünfmal so groß wie seine Gewichtskraft ist?

Fig. 4.15 Darstellung der Kräfte in der Horseshoe-Kurve.

\(\left| \vec{F}_{Z}\right| = 5\cdot \left|\vec{F}_G \right| \Leftrightarrow m\frac{v^2}{r} = 5 m g \Leftrightarrow r = \frac{v^2}{5g}\)

\(v = 145 \frac{km}{h} = 145 \cdot \frac{1000 \, m}{3600 \, s} = 40,23 \, \frac{m}{s} \)

\(r = \frac{\left( 40,23 \frac{m}{s}\right)^2}{5 \cdot 9,81 \frac{m}{s^2}} = 33 \, m\)