3. Dynamik#
Die Kinematik beschreibt Bewegungen durch mathematische Funktionen. Es werden Bewegungsgesetze betrachtet, ohne Kräfte zu berücksichtigen.Die Dynamik betrachtet die Ursache von Bewegungsänderungen und damit die Wirkung von Kräften. Grundsätzlich können innerhalb der Dynamik zwei Teilbereiche unterschieden werden. Zum einen die Statik, welche das Kräftegleichgewicht bei einem ruhenden Körper betrachtet, zum anderen die Kinetik, welche sich ändernde Bewegungszusände durch das Wirken von Kräften betrachtet.
Bei der Kinematik ging die Masse des Massenpunktes nicht in die Bewegungsgleichungen ein. In der Dynamik ist dies anders, hier geht die Masse in die relevanten Größen ein.
Wichtige Größen in der Dynamik sind
3.1. Masse#
Die Masse eines Körpers hat folgende Eigenschaften:
Masse ist ein Maß für die Trägheit. Dabei ist die Trägheit der Widerstand eines Körpers gegen eine Bewegungsänderung.
Die Masse ist unabhängig vom Ort, an dem sich ein Körper befindet und in der klassischen Mechanik unabhängig vom Bewegungszustand des Körpers.
Die Addition von Massen entspricht der Addition von Mengen \(\left( M = \sum_i m_i \right)\) (Extensive Größe).
Experimentell können Massen verglichen werden, indem auf zwei Körper mit den Massen \(m_1\) und \(m_2\) jeweils die gleiche Kraft wirkt und dann die Beschleunigungen \(a_1\) und \(a_2\), die den beiden Körpern erteilt werden gemessen werden.
Die physikalische Größe Masse hat außer der Eigenschaft Trägheit auch die Eigenschaft Schwere. Diese ist ein Maß für die gravitative Wechselwirkung.
Experimentell lässt sich kein Unterschied zwischen träger und schwerer Masse nachweisen.
Die SI Grundeinheit der Masse ist das Kilogramm
3.2. Kraft#
Um eine Kraft zu beschreiben muss nicht nur die Stärke der Kraft, also der Betrag, angegeben werden, vielmehr muss auch bekannt sein an welchem Punkt die Kraft angreift und in welche Richtung sie wirkt. Eine Kraft ist daher eine vektorielle Größe.
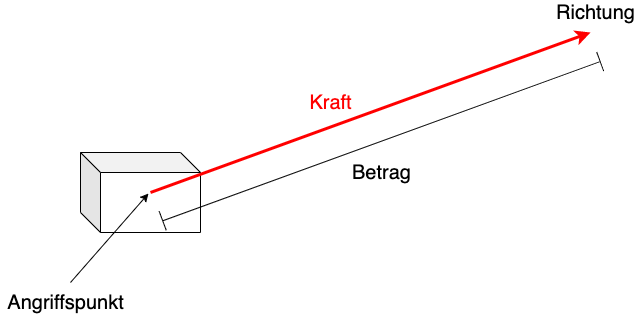
Fig. 3.2 Beschreibung der physikalischen Größe Kraft#
Beispiele für physikalische Kräfte:
Gewichtskraft \(\vec{F}_g = m \cdot \vec{g}\)
Auftriebskraft \(\vec{F}_A = \rho_{Wasser} \cdot V \cdot \vec{g}\)
Federkraft \(\vec{F}_F = -k \cdot \vec{x}\)
Graviationskraft \(\vec{F}_G = - G \frac{m_1 \cdot m_2}{r^2} \frac{\vec{r}}{r}\)
Coulombkraft \(\vec{F}_C = - e \frac{q_1 \cdot q_2}{r^2} \frac{\vec{r}}{r}\)
Haftreibung \(\vec{F}_R = - \mu_R \vec{F}_\perp\)
Kraft \(\vec{F}\) also ist eine vektorielle Größe, deren Richtung parallel zur Beschleunigung \(\vec{a}\) ist und deren Betrag
\(\left| \vec{F} \right| = m \cdot \left| \vec{a} \right|\)
definiert ist. Die Einheit der Kraft ist
\(\left[ F \right] = \text{1 Newton} = 1 \,N = 1 \, \frac{kg \cdot m}{s^2}\)
Für die Addition von Kräften und die Zerlegung einer Kraft in verschiedene Kraftrichtungen gelten die Regeln der Vektorrechnung. Allgemein gilt
\(\vec{F}_{ges} = \sum_{i=1}^N \vec{F}_i\)
3.3. Impuls#
Der Impuls \(\vec{p}\) ist eine vektorielle Zustandsgrösse und hat die Richtung der Geschwindigkeit.
\(\vec{p} = m \cdot \vec{v}\)
Für den Impuls gilt in einem festen Bezugssystem die Impulserhaltung.
\(\sum \vec{p}_{vorher} = \sum \vec{p}_{nachher}\)
