3.7. Reibungskräfte#
Reibungskräfte beschreiben die Rückwirkung auf seitlich angreifende Kräfte durch die Wechselwirkung von Oberflächen zueinander. Reibungskräfte wirken immer ihrer Ursache entgegen. In vielen Fällen können Reibungskräfte vernachlässigt werden, je nach Oberflächenbeschaffenheit können sie aber auch einen maßgeblichen Effekt haben.
Da Reibungskräfte hängen zum einen von der Oberflächenbeschaffenheit ab und zum anderen davon, wie stark die Oberflächen gegeneinander gedrückt werden. Die Wechselwirkung der Oberflächenbeschaffenheit wird durch einen experimentell zu ermittelnden Faktor \(\mu\) definiert und hängt immer von beiden wechselwirkenden Oberflächen ab. Dieser Faktor wird als Reibungskoeffizient bezeichnet. Beispiele für Reibungskoeffizienten sind zum Beispiel hier zu finden.
Reibungskräfte zwischen Festkörpern hängen linear von der Kraft \(\vec{F}_\perp\) ab, mit der die Oberflächen der Festkörper zusammengedrückt werden, der Linearitätskoeffizient ist der Reibungskoeffizient \(\mu\).
\(\left| \vec{F}_R \right| = \mu \left| \vec{F}_\perp \right|\)
Die Reibungskraft wirkt der Ursache entgegen, daher gilt
\(\vec{F}_R = - \mu \left| \vec{F}_\perp \right| \cdot \vec{e}_\parallel\)
3.7.1. Haftreibung#
Die Haftreibung wirkt zwischen zwei Oberflächen, wenn diese durch eine äußere Kraft zusammengedrückt werden und gleichzeitig eine seitliche Kraft \(F\) wirkt (siehe Abbildung 3.12).
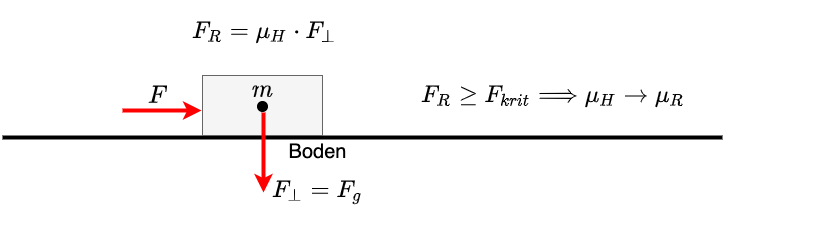
Fig. 3.12 Haftreibung#
Die Haftreibung ist gegeben durch
\(\vec{F}_R = - \mu_H \cdot F_\perp \cdot \vec{e}_\parallel\)
Diese Reibung wirkt der Kraft \(\vec{F}\) entgegen, und verhindert eine Relativbewegung der beiden Oberflächen. Wenn die Kraft \(\vec{F}\) einen kritischen Wert \(F_{krit}\) überscheitet, versetzt sich der Körper, an dem \(\vec{F}\) angreift, in Bewegung und die Haftreibung geht in Gleitreibung über. Kann der Gegenstand, ab dem \(\vec{F}\) angreift, rollen, geht die Haftreibung in Rollreibung über.
3.7.2. Gleit- und Rollreibung#
Gleitreibung tritt auf, wenn ein Körper durch eine Kraft gegen einen anderen Körper gedrückt wird und der eine Körper relativ zu dem anderen Körper gleitet. Gleitreibung sorgt damit für ein Abbremsen der Bewegung.
Die Gleitreibung ist gegeben durch
\(\vec{F}_R = - \mu_G \cdot F_\perp \cdot \vec{e}_\parallel\)
Die Gleitreibung ist gegeben durch
\(\vec{F}_R = - \mu_R \cdot F_\perp \cdot \vec{e}_\parallel\)
Im Allgemeinen gilt
\(\mu_H < \mu_G < \mu_R\)
3.7.3. Schiefe Ebene mit Reibung#
In Kapitel Schiefe Ebene wird die Schiefe Ebene ohne Reibung betrachtet. Im Folgenden werden die Bewegungsgleichungen für die Schiefe Ebene mit Reibung hergeleitet.
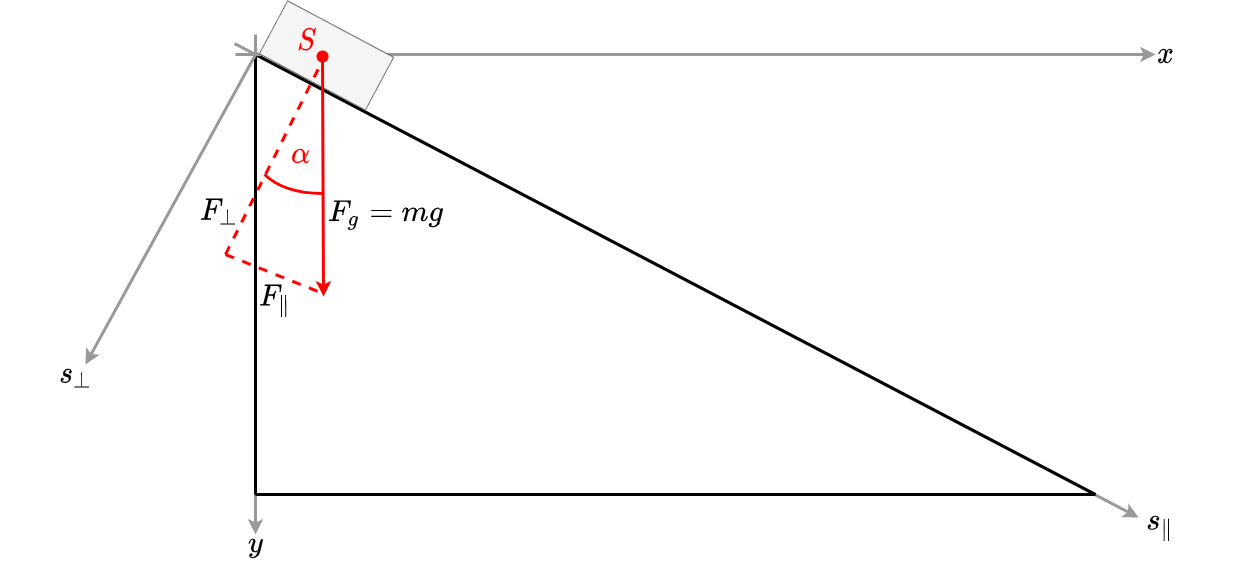
Fig. 3.13 Schiefe Ebene.#
In \(\parallel\)-Richtung wirkt nun die Kraft \(F_\parallel\) als sogenannte Hangabtriebskraft und ihr entgegen wird die Reibungskraft. Es gilt
\(F_{Hangabtrieb} = mg \cdot sin \left( \alpha \right)\)
\(F_R = - \mu_G \cdot F_\perp = - \mu_G \cdot mg \cdot cos \left( \alpha \right)\)
\(\Rightarrow F_\parallel = mg \cdot sin \left( \alpha \right) - \mu_G \cdot mg \cdot cos \left( \alpha \right)\)
Damit ergibt sich die Bewegungsgleichung in \(\parallel\)-Richtung
\(a = g \left( sin \left( \alpha \right) - \mu_G \cdot cos \left( \alpha \right) \right)\)
\(v(t) = g \cdot t \left( sin \left( \alpha \right) - \mu_G \cdot cos \left( \alpha \right) \right) \)
\(s(t) = \frac{1}{2} \cdot g \cdot t^2\left( sin \left( \alpha \right) - \mu_G \cdot cos \left( \alpha \right) \right) \)
